1 Analysis
Gegeben sind die in  definierten Funktionen
definierten Funktionen  und
und  mit
mit  und
und  Die Abbildung 1 zeigt deren Graphen sowie mit
Die Abbildung 1 zeigt deren Graphen sowie mit  und
und  zwei ihrer Schnittpunkte.
zwei ihrer Schnittpunkte.
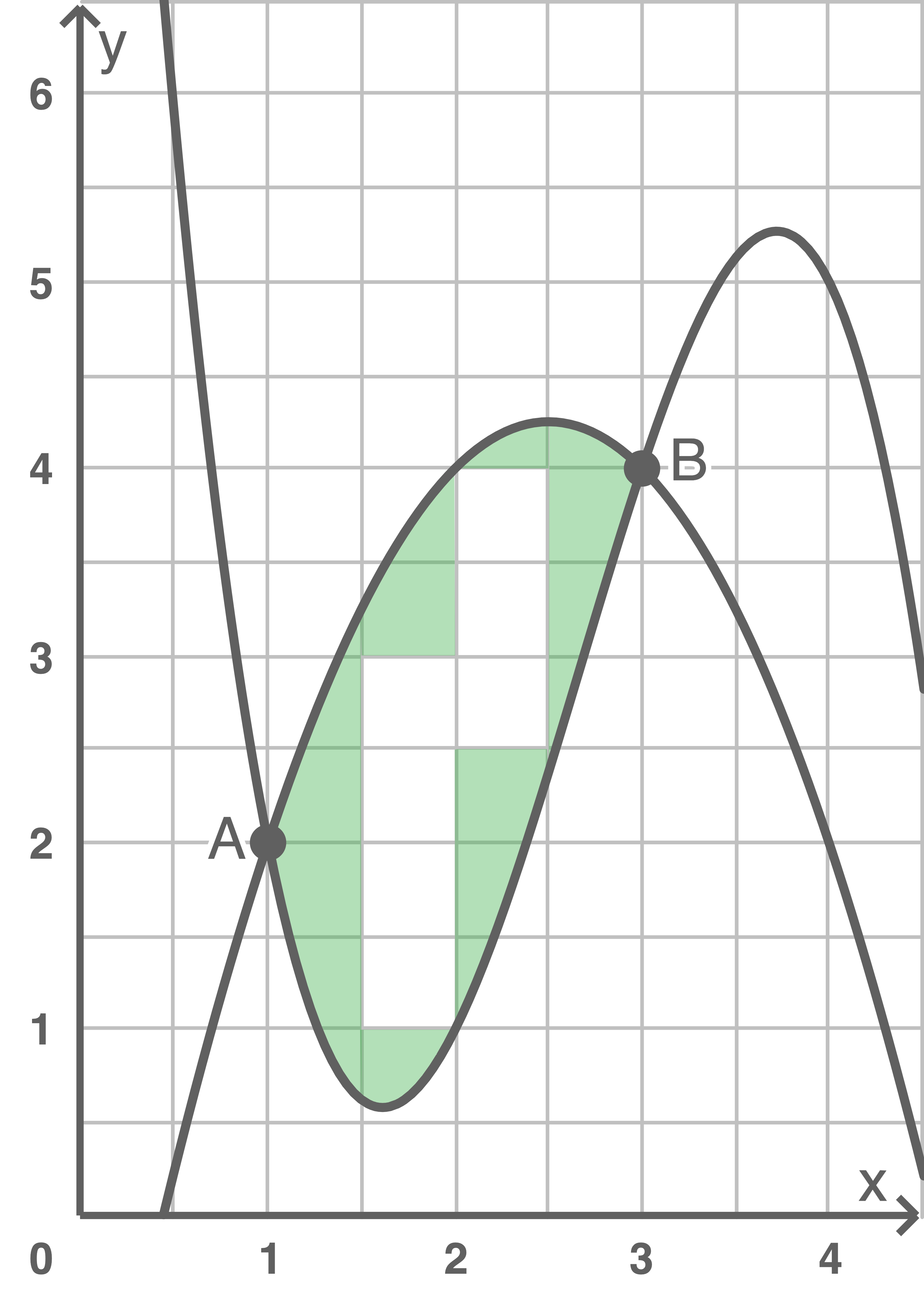

Abbildung 1
1.1
Berechne die Koordinaten des nicht abgebildeten Schnittpunkts der beiden Graphen und gib an, in welchem Quadranten des Koordinatensystems sich dieser befindet.
(3 BE)
1.2
Bestimme den Flächeninhalt der in der Abbildung grün markierten Fläche.
(5 BE)
1.3
Im Intervall  soll der größte vertikale Abstand beider Graphen berechnet werden. Peter behauptet:
Der größte Abstand muss an der Stelle des Hochpunktes von g oder an der Stelle des Tiefpunktes von
soll der größte vertikale Abstand beider Graphen berechnet werden. Peter behauptet:
Der größte Abstand muss an der Stelle des Hochpunktes von g oder an der Stelle des Tiefpunktes von  angenommen werden.
Beurteile seine Behauptung.
angenommen werden.
Beurteile seine Behauptung.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Der gesuchte Punkt befindet sich an der Stelle  Es gilt
Es gilt 
Der dritte Schnittpunkt befindet sich im IV. Quadranten.
befindet sich im IV. Quadranten.
Der dritte Schnittpunkt
1.2
Der Flächeninhalt der gesamten Fläche zwischen den Graphen von  und
und  zwischen ihren Schnittstellen
zwischen ihren Schnittstellen  und
und  wird mit Hilfe eines Integrals berechnet:
wird mit Hilfe eines Integrals berechnet:
 Ein einzelnes der sieben ausgenommenen Quadrate besitzt den Flächeninhalt
Ein einzelnes der sieben ausgenommenen Quadrate besitzt den Flächeninhalt  Der gesuchte Flächeninhalt beträgt somit
Der gesuchte Flächeninhalt beträgt somit ![\(4-7 \cdot 0,25=2,25\,\text{[FE]}.\)](https://mathjax.schullv.de/5df4e32148d580498769efbc56181902879c8a994a2053b21977c2b3d0fa075d?color=5a5a5a)
1.3
Peters Aussage ist falsch.
Anhand der Graphen ist zu erkennen, dass die zugehörigen vertikalen Abstände an den Stellen (Tiefpunkt von
(Tiefpunkt von  ) und
) und  (Hochpunkt von
(Hochpunkt von  ) kleiner sind als der betrachtete Abstand an der Stelle
) kleiner sind als der betrachtete Abstand an der Stelle  Alternativ
Unmittelbar hinter dem Tiefpunkt von
Alternativ
Unmittelbar hinter dem Tiefpunkt von  gibt es ein Intervall, in dem der Graph von
gibt es ein Intervall, in dem der Graph von  einen größeren Anstieg hat als der Graph von
einen größeren Anstieg hat als der Graph von 
Demzufolge wird der vertikale Abstand hinter dem Tiefpunkt der Graphen zunächst größer, da der Graph von stärker ansteigt als der von
stärker ansteigt als der von  Analog gilt dies auch für ein Intervall vor der Stelle des Hochpunkts des Graphen von
Analog gilt dies auch für ein Intervall vor der Stelle des Hochpunkts des Graphen von 
Anhand der Graphen ist zu erkennen, dass die zugehörigen vertikalen Abstände an den Stellen
Demzufolge wird der vertikale Abstand hinter dem Tiefpunkt der Graphen zunächst größer, da der Graph von