Pflichtaufgabe A0
1 Analysis
Gegeben ist die Zahlenfolge
1.1
Berechne  .
.
(2 BE)
1.2
Die Glieder von  können auch mit Hilfe der Gleichung
können auch mit Hilfe der Gleichung 
 berechnet werden. Bestimme die Werte für
berechnet werden. Bestimme die Werte für  und
und  .
.
(3 BE)
2 Analysis
Gegeben ist die Funktion
2.1
Berechne die Stelle  , an der die Gerade mit der Gleichung
, an der die Gerade mit der Gleichung  eine Tangente an
eine Tangente an  ist.
ist.
(2 BE)
2.2
Die  -Achse und
-Achse und  begrenzen eine Fläche vollständig. Begründe, dass der Inhalt dieser Fläche kleiner als
begrenzen eine Fläche vollständig. Begründe, dass der Inhalt dieser Fläche kleiner als  ist.
ist.
(3 BE)
3 Analytische Geometrie
Gegeben sind die Punkte
3.1
Bestimme  so, dass der Punkt
so, dass der Punkt  auf der Geraden
auf der Geraden  liegt.
liegt.
(2 BE)
3.2
Der Punkt  liegt in der Ebene
liegt in der Ebene  .
Bestimme die Koordinaten eines Punktes, der einen Abstand von
.
Bestimme die Koordinaten eines Punktes, der einen Abstand von  zu dieser Ebene besitzt.
zu dieser Ebene besitzt.
(3 BE)
4 Stochastik
In einer Urne befinden sich vier Kugeln, die mit den Zahlen
4.1
Begründe, dass die Wahrscheinlihckeit der Werte von  nicht gleichverteilt sind.
nicht gleichverteilt sind.
(2 BE)
4.2
Bestimme den Erwartungswert von  .
.
(3 BE)
1 Analysis
1.1
1.2
2 Analysis
2.1
besitzt die gleiche Steigung
wie
an der Stelle
.
besitzt an der Stelle
den gleichen Funktionswert wie
.
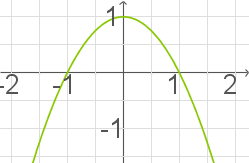
2.2
Eine Skizze kann dir bei der Begründung helfen. Der Scheitelpunkt der Parabel hat die Koordinaten  . Der Graph schneidet an den Stellen
. Der Graph schneidet an den Stellen  und
und  die
die  -Achse. Die Fläche, die der Graph mit der
-Achse. Die Fläche, die der Graph mit der  -Achse einschließt liegt vollständig innerhalb des Rechtecks, das von den Geraden
-Achse einschließt liegt vollständig innerhalb des Rechtecks, das von den Geraden  ,
,  und
und  und der
und der  -Achse eingeschlossen wird, füllt dieses aber nicht aus.
-Achse eingeschlossen wird, füllt dieses aber nicht aus.
3 Analytische Geometrie
3.1
1. Schritt: Gleichung der Geraden  aufstellen
aufstellen

![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OA} + t\cdot \overrightarrow{AB}\\[5pt]
&=& \pmatrix{4\\2\\6}+t\cdot \pmatrix{2\\1\\2 } \\[5pt]
\end{array}\)](https://mathjax.schullv.de/199d0762456a5897ea2e1c5310ddd93d4292f03679d6807cc5da2a09f243ba59?color=5a5a5a) 2. Schritt: Gleichungssystem aufstellen
Durch Einsetzen des Ortsvektors von Punkt
2. Schritt: Gleichungssystem aufstellen
Durch Einsetzen des Ortsvektors von Punkt  in die Geradengleichung folgt:
in die Geradengleichung folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{OC} &=&\pmatrix{4\\2\\6}+t\cdot \pmatrix{2\\1\\2 } \\[5pt]
\pmatrix{2\\1\\z} &=& \pmatrix{4\\2\\6}+t\cdot \pmatrix{2\\1\\2 } \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e2974333504f42778fc7b54cf5f19ef36ff40ca56be92ad1f8f5ae526a07391d?color=5a5a5a) Aus der
Aus der  -Koordinate der Gleichung ergibt sich:
-Koordinate der Gleichung ergibt sich:
![\(\begin{array}[t]{rll}
2&=&4 +t\cdot 2 &\quad \scriptsize \mid\; -4 \\[5pt]
-2&=& 2t &\quad \scriptsize \mid\;: 2 \\[5pt]
-1&=&t
\end{array}\)](https://mathjax.schullv.de/d7d3c1cbb7497d51a32f299f9ec5205385a62f8329835dbbd922b11f4dd9623f?color=5a5a5a) Aus der
Aus der  -Koordinate folgt nun:
-Koordinate folgt nun:
![\(\begin{array}[t]{rll}
z&=&6+ t\cdot 2 &\quad \scriptsize \mid\; t= -1 \\[5pt]
&=&6+ (-1)\cdot 2 \\[5pt]
&=& 4
\end{array}\)](https://mathjax.schullv.de/00b53f194bcf0ea16b7b3f4452f35c4e5b2f26c7855d5aa0d1c75cadaeb4c7f4?color=5a5a5a) Für
Für  liegt der Punkt
liegt der Punkt  somit auf der Geraden
somit auf der Geraden 
3.2
1. Schritt: Normalenvektor der Ebene bestimmen
Ein Normalenvektor der Ebene kann direkt aus der Koordinatenform abgelesen werden:
 Die Länge des Normalenvektors beträgt:
Die Länge des Normalenvektors beträgt:
![\(\begin{array}[t]{rll}
\left| \overrightarrow{n}\right| &=&\sqrt{1^2+2^2+2^2} & \\[5pt]
&=& 3
\end{array}\)](https://mathjax.schullv.de/c92d6d5b441cf05441d7b14be67a64de47f4420db3d001838605d77dc9652034?color=5a5a5a) 2. Schritt: Punkt mit dem Abstand 6 ermitteln
Durch zweifaches Addieren des gewählten Normalenvektors der Ebene zu den Koordinaten des Punktes
2. Schritt: Punkt mit dem Abstand 6 ermitteln
Durch zweifaches Addieren des gewählten Normalenvektors der Ebene zu den Koordinaten des Punktes  ergeben sich die Koordinaten eines Punktes mit dem Abstand
ergeben sich die Koordinaten eines Punktes mit dem Abstand  zur Ebene:
zur Ebene:
![\(\begin{array}[t]{rll}
\overrightarrow{OP}&=& \overrightarrow{OA} + 2 \cdot \overrightarrow{n} & \\[5pt]
&=& \pmatrix{6\\6\\10}
\end{array}\)](https://mathjax.schullv.de/e8b27f54996c90287349a77e763267d9e7351c15ba05d53fad5afaf06db51808?color=5a5a5a) Der Punkt
Der Punkt  hat folglich den Abstand
hat folglich den Abstand  zur Ebene
zur Ebene 
4 Stochastik
4.1
Das Ergebnis
4.2
© 2017 - SchulLV.