3 Analytische Geometrie
Die Zuschauertribüne eines Freilichttheaters kann durch das Viereck  mit den Eckpunkten
mit den Eckpunkten 

 und
und  in der Ebene
in der Ebene  modelliert werden. Die
modelliert werden. Die  -Ebene stellt den Erdboden dar. Die Längeneinheit ist
-Ebene stellt den Erdboden dar. Die Längeneinheit ist 
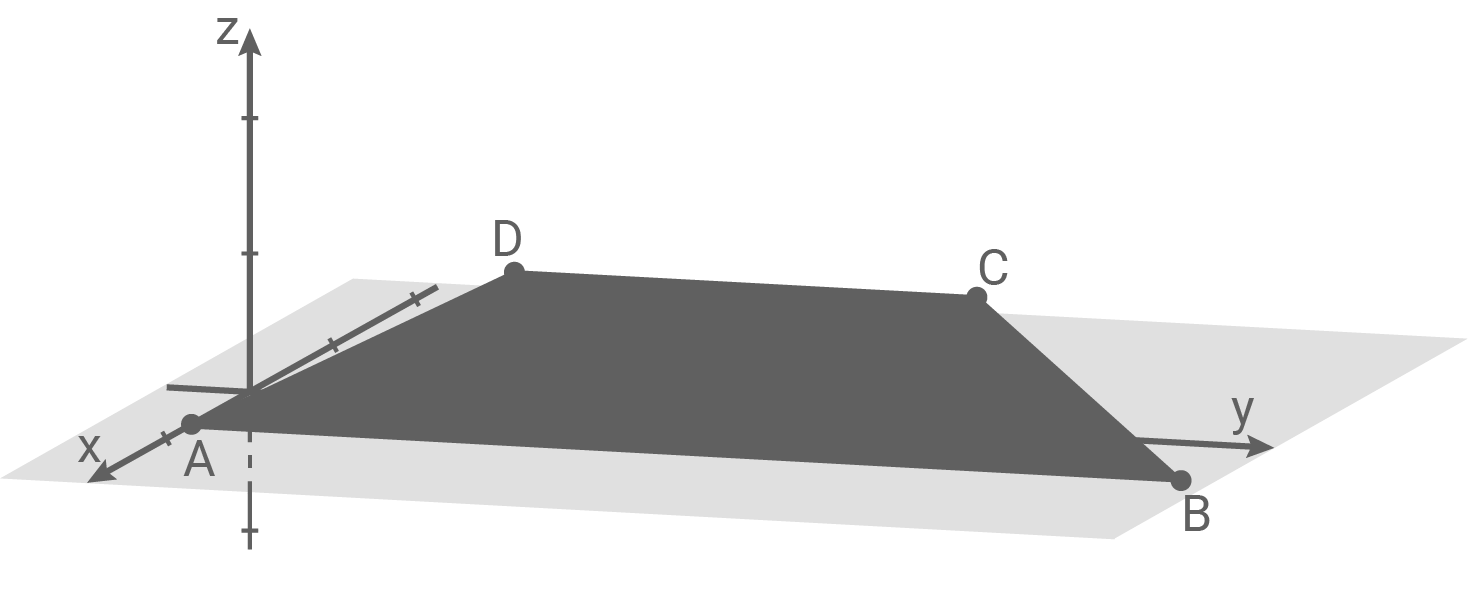

Abbildung 1
3.1
Zeige, dass das Viereck  ein Trapez ist, in dem zwei gegenüberliegende Seiten gleich lang sind.
ein Trapez ist, in dem zwei gegenüberliegende Seiten gleich lang sind.
(3 BE)
3.2
Ermittle eine Gleichung der Ebene  in Koordinatenform.
(Zur Kontrolle:
in Koordinatenform.
(Zur Kontrolle:  )
)
(3 BE)
3.3
Berechne den Neigungswinkel der Zuschauertribüne gegenüber dem Erdboden.
(2 BE)
3.4
Peter schaut in Richtung eines Turms. Im Modell blickt er vom Punkt  in Richtung des Punkts
in Richtung des Punkts 
Im Punkt liegt im Modell die Spitze dieses Turms.
Weise mithilfe der Abbildung 2 nach, dass die Sicht auf die Turmspitze durch die Zuschauertribüne nicht eingeschränkt ist.
liegt im Modell die Spitze dieses Turms.
Weise mithilfe der Abbildung 2 nach, dass die Sicht auf die Turmspitze durch die Zuschauertribüne nicht eingeschränkt ist.
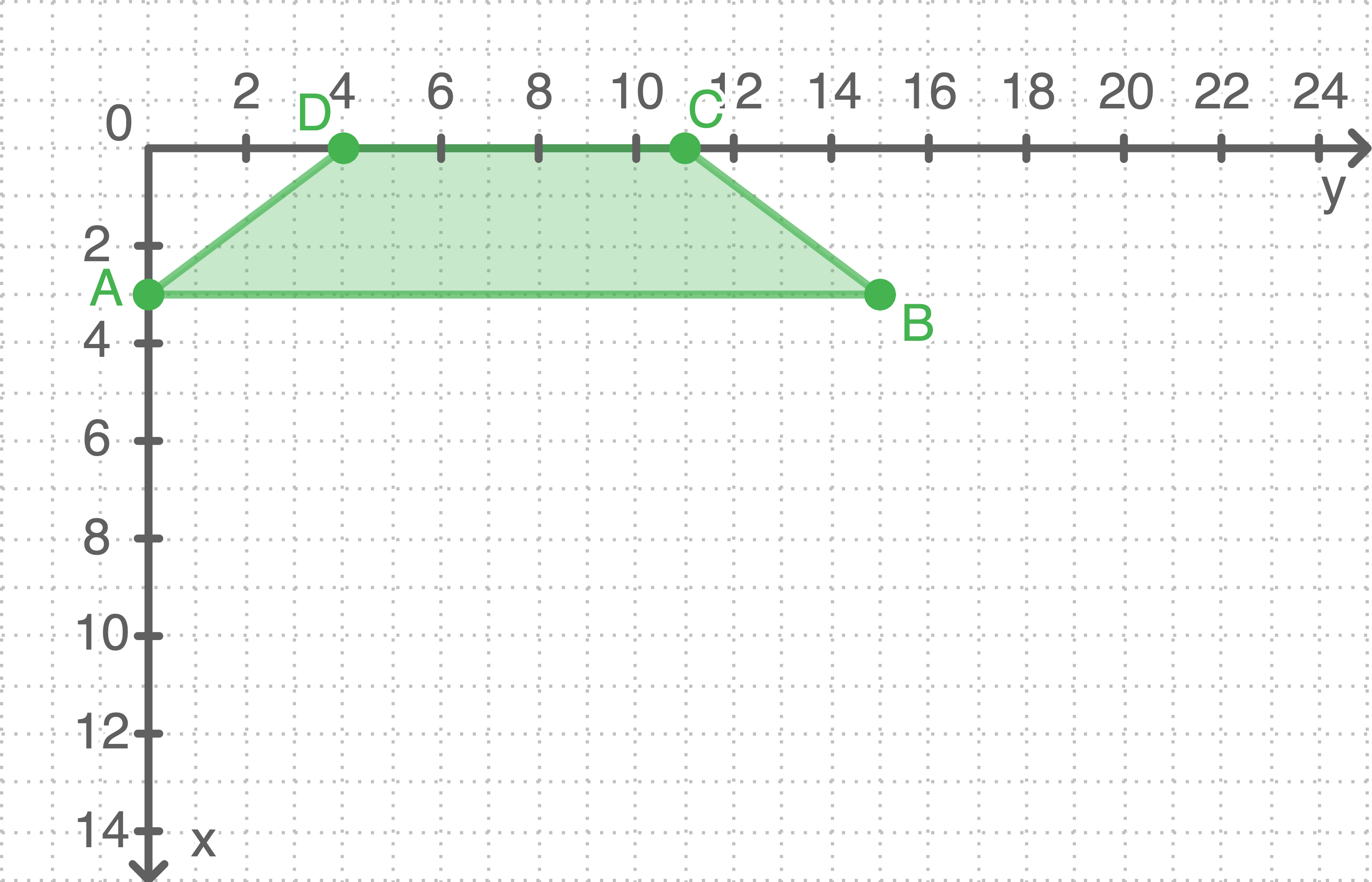
Im Punkt

Abbildung 2
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
Trapezform zeigen

 Es gilt also
Es gilt also  Die beiden Vektoren sind linear abhängig und die gegenüberliegenden Seiten
Die beiden Vektoren sind linear abhängig und die gegenüberliegenden Seiten  und
und  daher parallel.
Gleiche Länge zweier gegenüberliegenden Seiten zeigen
Die gegenüberliegenden Seiten
daher parallel.
Gleiche Länge zweier gegenüberliegenden Seiten zeigen
Die gegenüberliegenden Seiten  und
und  sind also gleich lang.
sind also gleich lang.
3.2
Mit dem Kreuzprodukt und dem CAS kann ein Normalenvektor von  bestimmt werden:
Einsetzen der Koordinaten von
bestimmt werden:
Einsetzen der Koordinaten von  und
und  in die allgemeine Ebenengleichung in Koordinatenform:
in die allgemeine Ebenengleichung in Koordinatenform:
 Die Koordinatengleichung der Ebene lautet demnach
Die Koordinatengleichung der Ebene lautet demnach 
3.3
3.4
Der Blick von Peter in Richtung der Turmspitze kann durch einen Teil der folgenden Gerade beschrieben werden:
![\(\begin{array}[t]{rll}
g: \, \overrightarrow{x}&=& \overrightarrow{OP} + s\cdot \overrightarrow{PS} \\[5pt]
&=& \pmatrix{11\\ 0\\1,5} + t\cdot \pmatrix{-600\\ 1200\\28,5}
\end{array}\)](https://mathjax.schullv.de/c81f208639070bef8dbaa7eaf0a305b51f67c921ca31259496e91b16815a0687?color=5a5a5a) Der Richtungsvektor kann auch gekürzt werden:
Der Richtungsvektor kann auch gekürzt werden:
 So lässt sich die Gerade in die Abbildung einzeichnen:
So lässt sich die Gerade in die Abbildung einzeichnen:
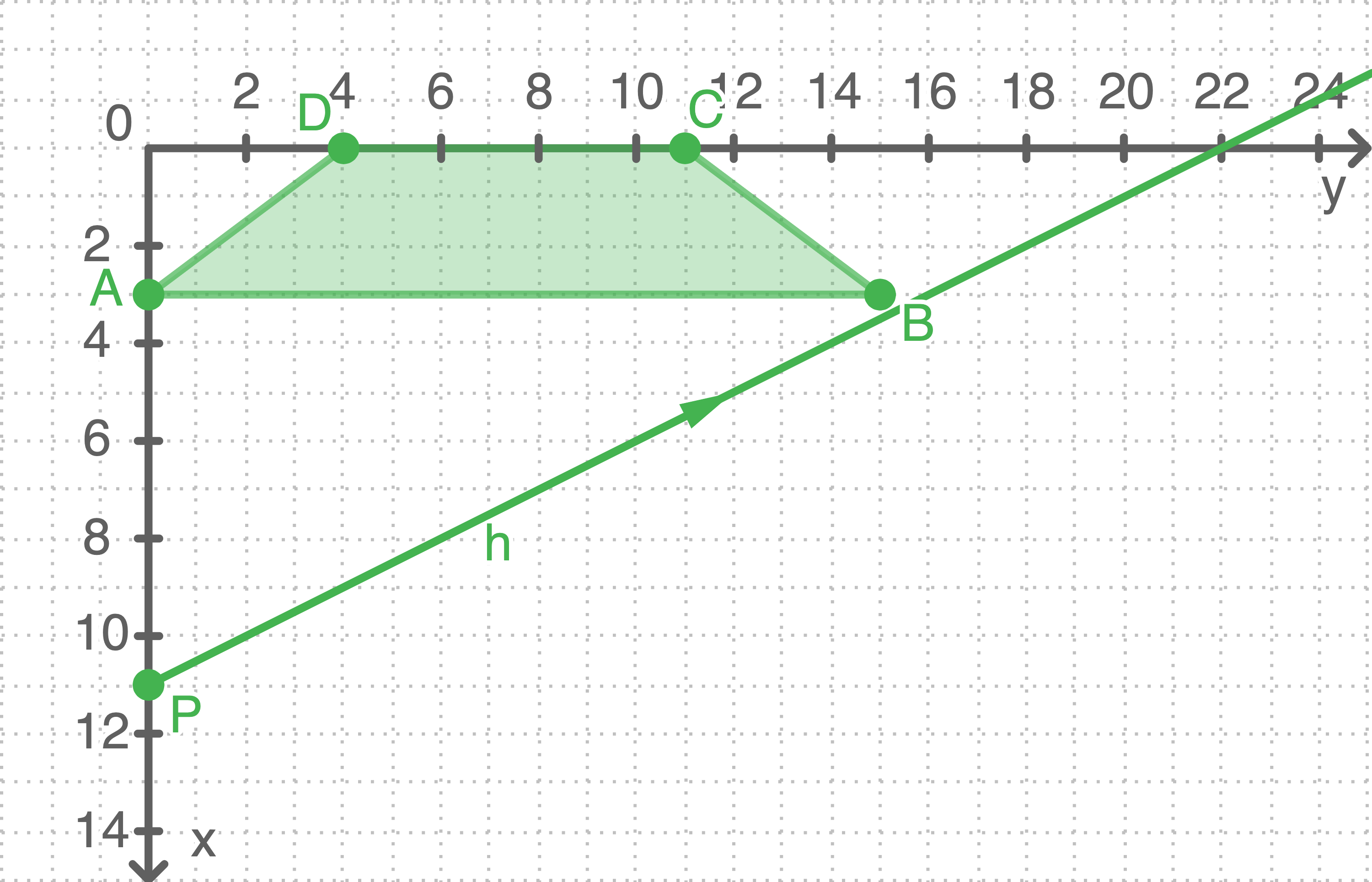 Peters Blick geht also knapp an der Tribüne vorbei. Seine Sicht ist durch die Tribüne nicht eingeschränkt.
Peters Blick geht also knapp an der Tribüne vorbei. Seine Sicht ist durch die Tribüne nicht eingeschränkt.
