Pflichtaufgaben
Analysis
1
Die Abbildung zeigt die Graphen einer in 
definierten Funktion 
mit der Gleichung 
und deren erster Ableitungsfunktion.
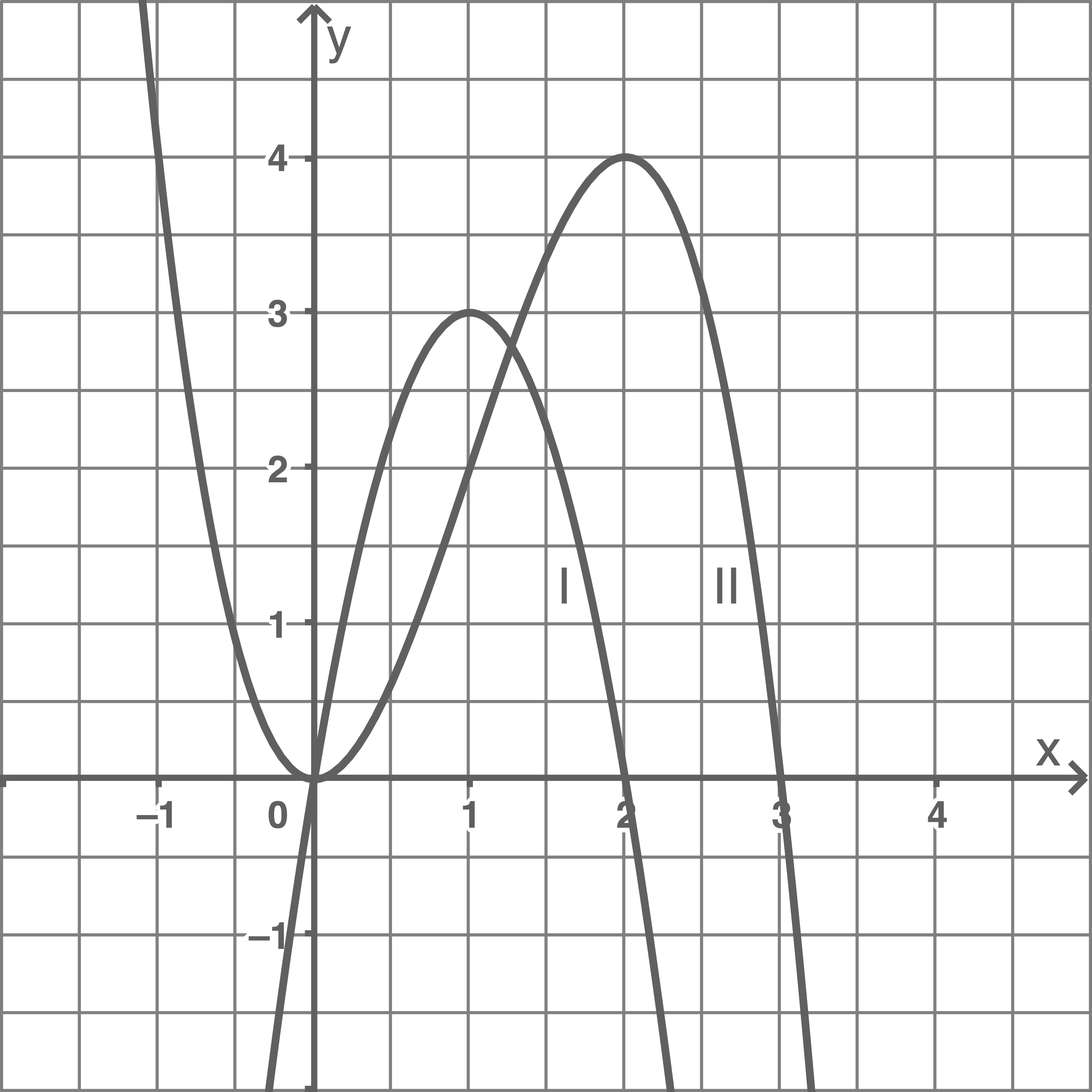
1.1
Gib an, welcher der beiden Graphen die Ableitungsfunktion darstellt. Begründe deine Entscheidung.
(2 BE)
1.2
Ermittle rechnerisch eine Gleichung der Tangente an den Graphen von im Punkt 
(3 BE)
2
Gegeben sind die in definierten Funktionen 
und 
mit 
und 
Ihre Graphen sind
und 
Die Abbildung zeigt den Graphen
Ihre Graphen sind
Die Abbildung zeigt den Graphen
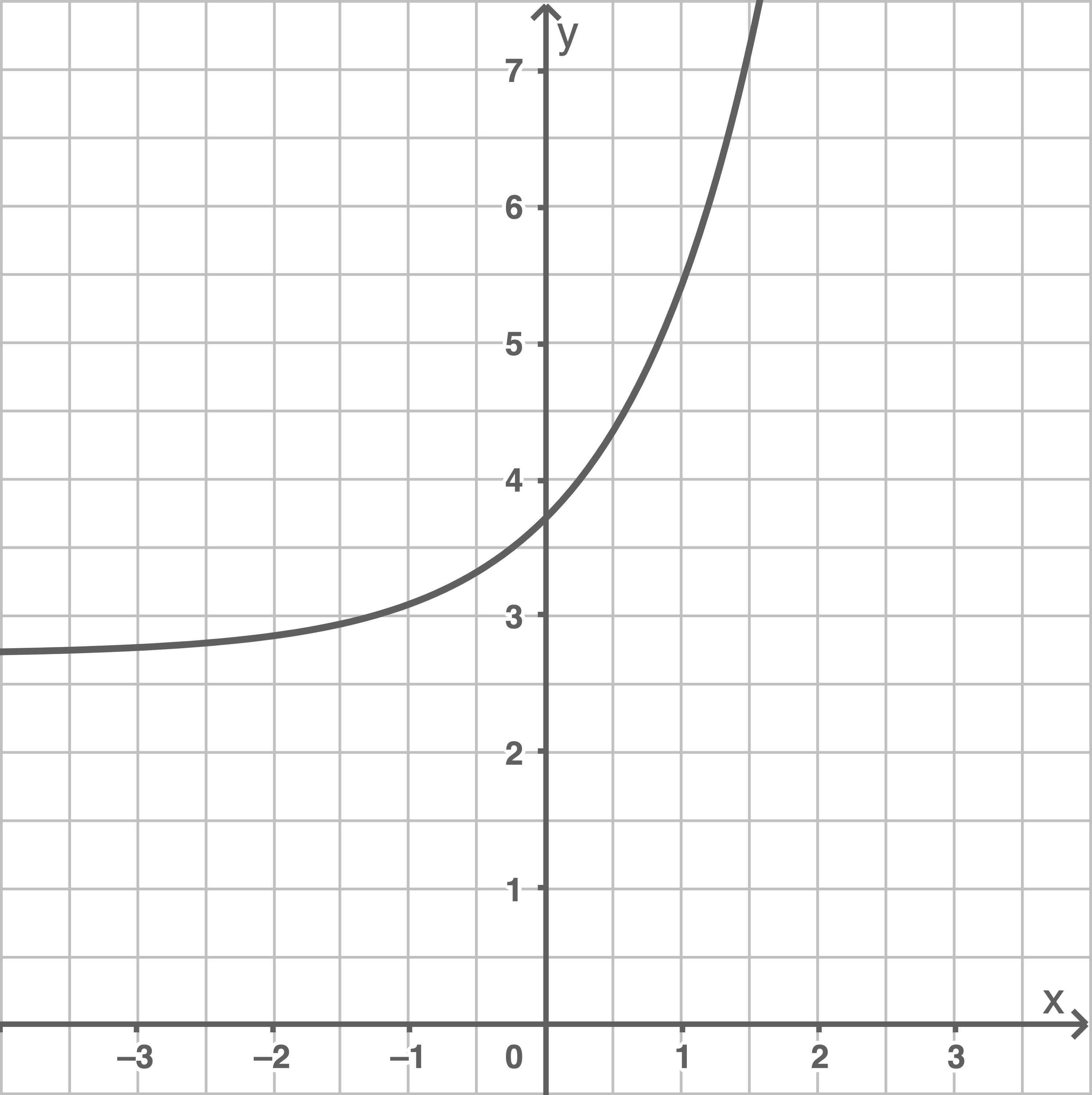
2.1
Gib eine Gleichung der Asymptote von an.
(1 BE)
2.2
Bestimme die 
-Koordinate des Schnittpunktes von und
(2 BE)
2.3
Zeichne 
in die Abbildung ein.
(2 BE)
Analytische Geometrie
3
Gegeben sind die Punkte 
und 
wobei 
eine positive reelle Zahl ist.
3.1
Zeige, dass es sich beim Dreieck 
um ein gleichschenkliges Dreieck mit der Basis 
handelt.
(2 BE)
3.2
Das Dreieck hat den Flächeninhalt 35. Bestimme den Wert von 
(3 BE)
4
Gegeben ist die Ebene 
4.1
Prüfe, ob der Punkt 
in 
liegt.
(1 BE)
4.2
Beschreibe die besondere Lage von im Koordinatensystem.
(2 BE)
4.3
Bestimme diejenige reelle Zahl 
, für die die Ebene 
senkrecht zu steht.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Graph I stellt die Ableitungsfunktion dar. Der Graph II hat an den Stellen 0 und 2 Extrempunkte, Graph I schneidet an diesen Stellen die -Achse.
1.2
Koordinaten des Berührpunkts berechnen: 
Allgemeine Geradengleichung der Tangente: 
Steigung 
berechnen:
Einsetzen der Steigung sowie der Koordinaten des Punkts 
in die allgemeine Geradengleichung der Tangente ergibt:
, daraus folgt 
und damit 
2.1
Gleichung der Asymptote von : 
, da 
2.2
Gleichsetzen ergibt:
![\(\begin{array}[t]{rll}
\mathrm e^x+\mathrm e&=&2\cdot \mathrm e^x \quad \scriptsize \mid\;-\mathrm e^x \\[5pt]
\mathrm e&=&\mathrm e^x\\
x&=&1
\end{array}\)](https://mathjax.schullv.de/b34e92e77b2c2b2126922608b9c3929d533b5c8b5d0b5fd7393ed3f2774a9723?color=5a5a5a)
2.3
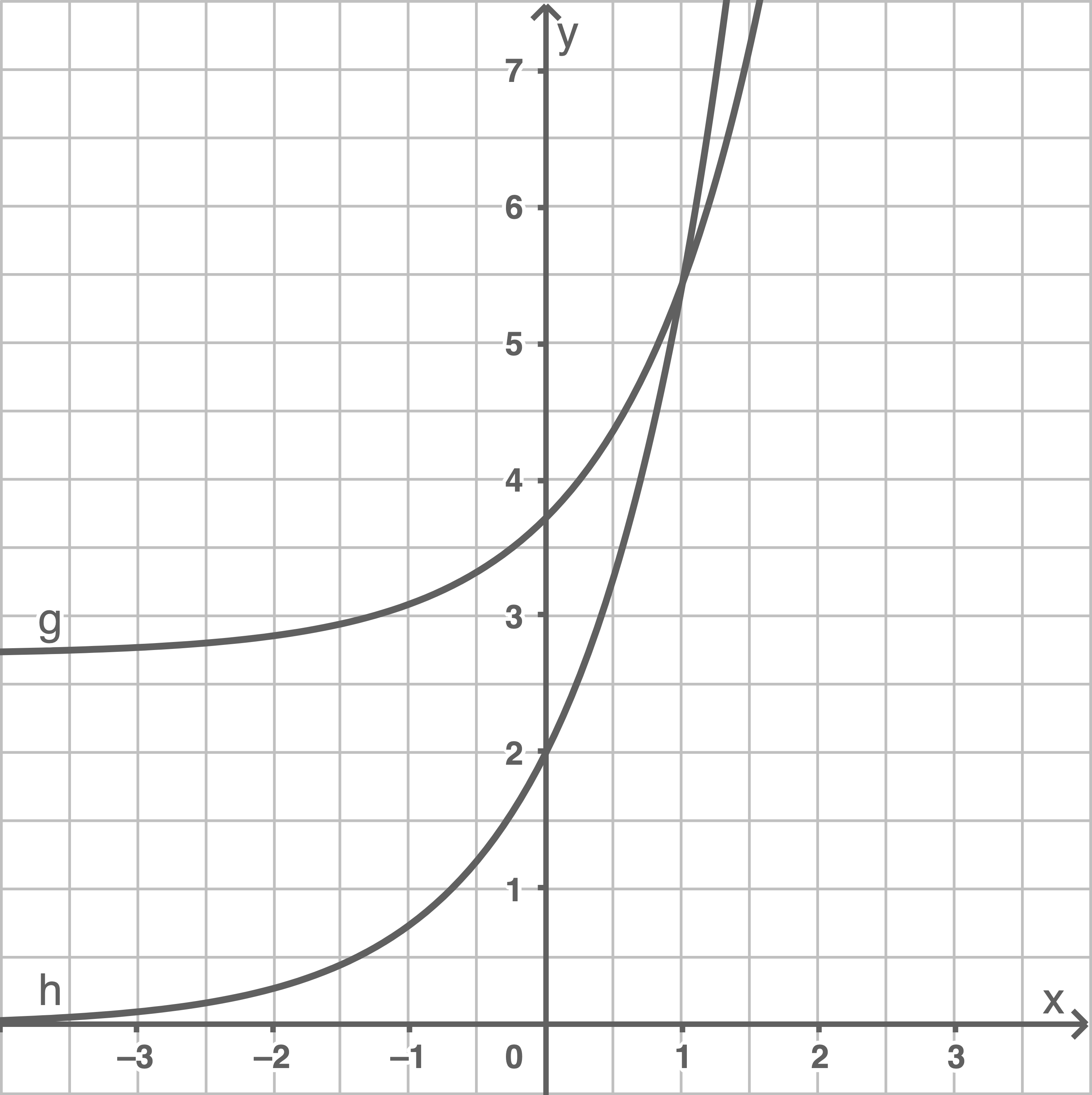
3.1
Damit das Dreieck gleichschenklig ist, müssen die beiden Seiten 
und 
gleich lang sein.
Somit ist gezeigt, dass das Dreieck gleichschenklig ist.
3.2
Mittelpunkt von ist 
also 
Damit kann die Höhe des Dreiecks berechnet werden.
Der Flächeninhalt des Dreiecks lässt sich berechnen mit:
also 
und somit 
4.1
Punkt in einsetzen:
also 
Dies ist korrekt, also liegt der Punkt in 
4.2
4.3
Damit die Ebenen zueinander senkrecht stehen, muss das Skalarprodukt der jeweiligen Normalenvektoren gleich Null sein.
daraus folgt 