1 Analysis
1.1
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Ihr Graph heißt
Ihr Graph heißt 
1.1.1
Der Graph  hat den Tiefpunkt
hat den Tiefpunkt  und den Hochpunkt
und den Hochpunkt  Berechne die Koordinaten von
Berechne die Koordinaten von  und
und 
Zur Kontrolle:  -Koordinaten
-Koordinaten 
(4 BE)
1.1.2
Zeichne  für
für  in ein Koordinatensystem.
in ein Koordinatensystem.
(3 BE)
1.1.3
Gib das Monotonieverhalten von  an.
an.
(2 BE)
1.1.4
Die Funktion  hat die drei Nullstellen
hat die drei Nullstellen  und
und  . Gib den Wert von
. Gib den Wert von  an und begründe deine Angabe.
an und begründe deine Angabe.
(2 BE)
1.1.5
An  wird im Koordinatenursprung die Tangente
wird im Koordinatenursprung die Tangente  gelegt. Bestimme eine Gleichung von
gelegt. Bestimme eine Gleichung von 
(2 BE)
1.1.6
Betrachtet wird die Funktionsschar  mit
mit  Für
Für  ergibt sich die Funktion
ergibt sich die Funktion  aus den vorherigen Teilaufgaben. Ermittle die Anzahl der Nullstellen von
aus den vorherigen Teilaufgaben. Ermittle die Anzahl der Nullstellen von  in Abhängigkeit vom Wert des Parameters
in Abhängigkeit vom Wert des Parameters 
(4 BE)
1.2
Ein Wasserbecken füllt sich innerhalb von  Stunden in unterschiedlicher Intensität. Der Graph der reellen Funktion
Stunden in unterschiedlicher Intensität. Der Graph der reellen Funktion  modelliert für
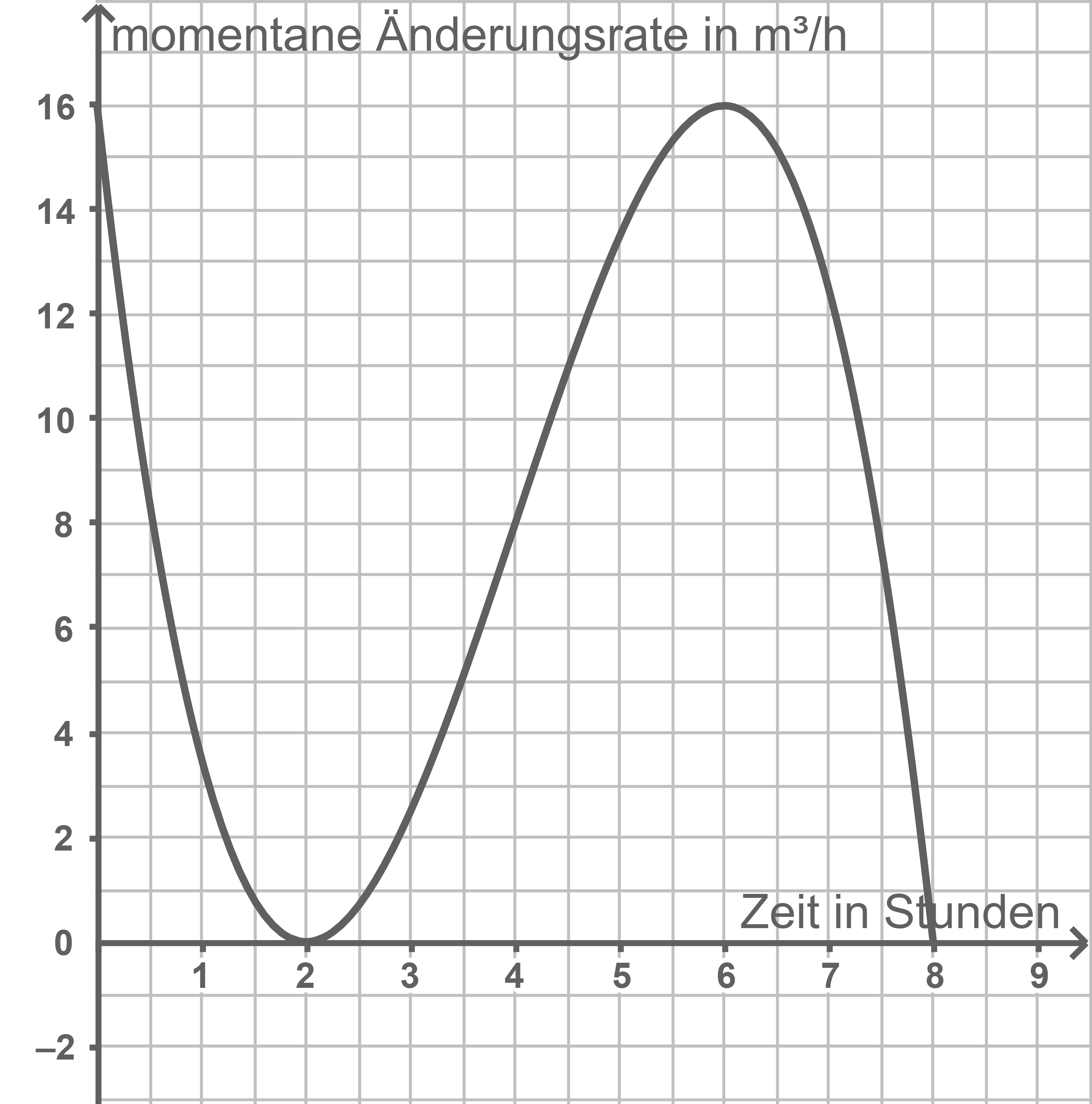
modelliert für  die zeitliche Entwicklung der momentanen Änderungsrate des Wasservolumens im Becken (siehe Abbildung). Dabei gibt
die zeitliche Entwicklung der momentanen Änderungsrate des Wasservolumens im Becken (siehe Abbildung). Dabei gibt  die seit Beobachtungsbeginn vergangene Zeit in Stunden
die seit Beobachtungsbeginn vergangene Zeit in Stunden  und
und  die momentane Änderungsrate in Kubikmeter pro Stunde
die momentane Änderungsrate in Kubikmeter pro Stunde  an. Die Beobachtung beginnt um
an. Die Beobachtung beginnt um  Uhr.
Uhr.
1.2.1
Es gibt zwei Zeitpunkte, zu denen die momentane Änderungsrate minimal ist. Gib einen dieser Zeitpunkte an.
(1 BE)
1.2.2
Begründe mit Hilfe der Abbildung, dass das Wasservolumen im Becken zu keinem Zeitpunkt abnimmt.
(2 BE)
1.2.3
Gib zwei Zeitintervalle an, in denen die momentane Änderungsrate des Wasservolumens höchstens  beträgt.
beträgt.
(3 BE)
1.2.4
Bestimme mit Hilfe der Abbildung das Volumen des Wassers, das in den ersten zwei Stunden in das Wasserbecken einströmt.
(3 BE)
1.2.5
Die Funktion  ist eine ganzrationale Funktion 3. Grades. Ermittle eine Gleichung von
ist eine ganzrationale Funktion 3. Grades. Ermittle eine Gleichung von  berücksichtige dazu die folgenden Eigenschaften ihres Graphen. Der Graph von
berücksichtige dazu die folgenden Eigenschaften ihres Graphen. Der Graph von  hat
hat
- den Schnittpunkt mit der
-Achse
- einen Tiefpunkt bei
- einen Wendepunkt bei
und
- eine Steigung von
an der Stelle
(6 BE)
1.2.6
Im Folgenden wird der Lösungsweg einer Aufgabe im Sachzusammenhang dargestellt.

 Formuliere dazu eine passende Aufgabenstellung.
Formuliere dazu eine passende Aufgabenstellung.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
1.1.1
Für die erste Ableitung von  ergibt sich:
ergibt sich:
 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/a505e575a27149887cdcb91b60ad50d1b994cc45f66f0994db30ffe00dfb9ad1?color=5a5a5a) Da laut Aufgabenstellung zwei Extremstellen existieren, kann die Überprüfung der hinreichenden Bedingung hier vernachlässigt werden.
2. Schritt: Funktionswerte bestimmen
Da laut Aufgabenstellung zwei Extremstellen existieren, kann die Überprüfung der hinreichenden Bedingung hier vernachlässigt werden.
2. Schritt: Funktionswerte bestimmen
![\(\begin{array}[t]{rll}
f(2)&=&\dfrac{1}{2}\cdot2^3-6\cdot2 \\[5pt]
&=&4-12 \\[5pt]
&=&-8
\end{array}\)](https://mathjax.schullv.de/3771e1a520b1d05e0f5447c11e17b66be6061892d381331ea82a81a1b7fc7832?color=5a5a5a)
![\(\begin{array}[t]{rll}
f(-2)&=&\dfrac{1}{2}\cdot(-2)^3-6\cdot(-2) \\[5pt]
&=&-4+12 \\[5pt]
&=&8
\end{array}\)](https://mathjax.schullv.de/487e52048097f27db41486f2ef936e6d1c445c9aeb1a269f407dcec78abbd270?color=5a5a5a) Da die Funktion nur einen Hochpunkt und einen Tiefpunkt besitzt, muss die
Da die Funktion nur einen Hochpunkt und einen Tiefpunkt besitzt, muss die  -Koordinate des Hochpunktes größer als die des Tiefpunktes sein. Somit folgt für die gesuchten Koordinaten
-Koordinate des Hochpunktes größer als die des Tiefpunktes sein. Somit folgt für die gesuchten Koordinaten  und
und 
1.1.2
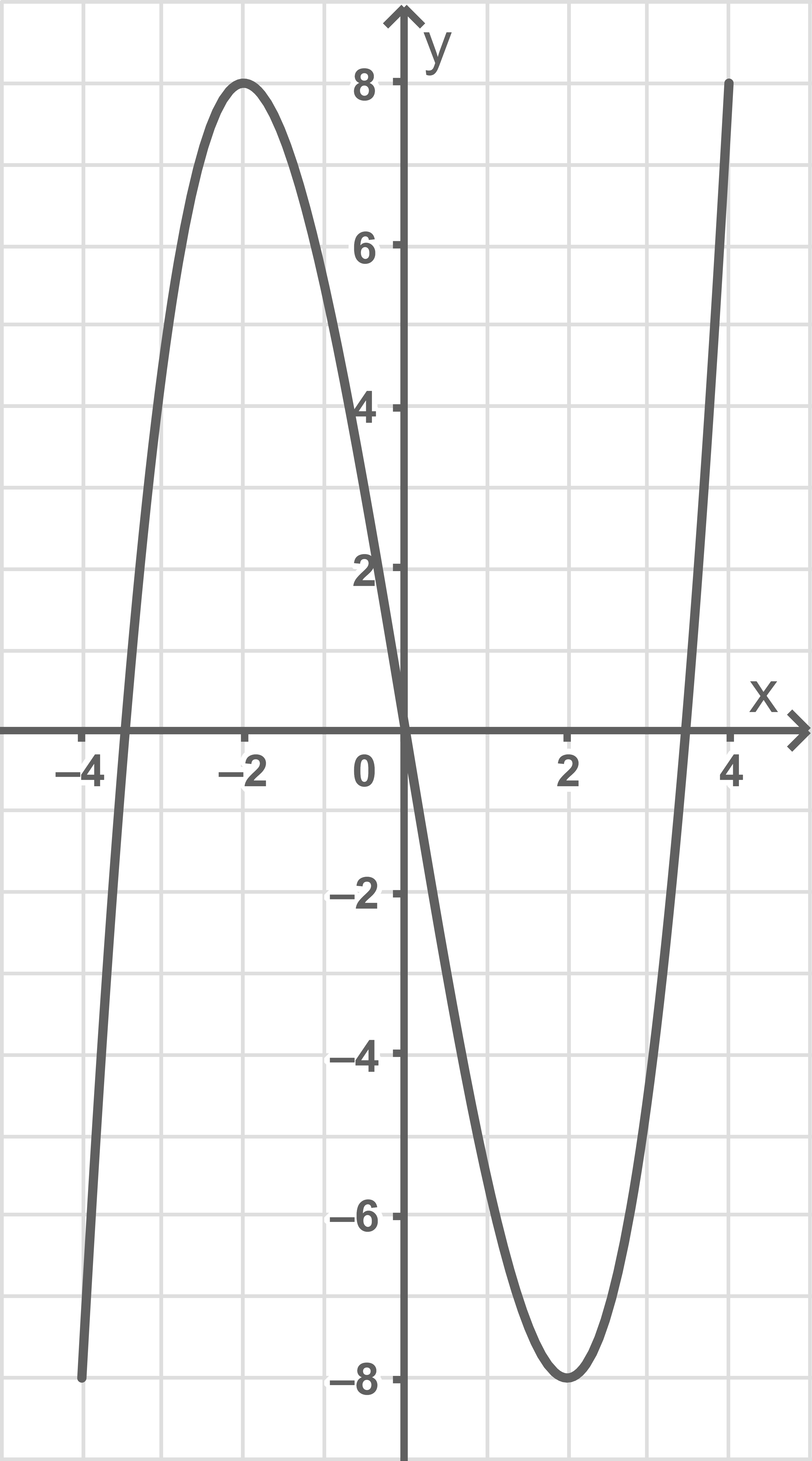
1.1.3
Die Funktion  ist monoton steigend für
ist monoton steigend für  sowie
sowie  und monoton fallend für
und monoton fallend für 
1.1.4
Es gilt  da
da  punktsymmetrisch zum Ursprung ist.
punktsymmetrisch zum Ursprung ist.
1.1.5
Die gesuchte Tangente hat die allgemeine Form  Einsetzen von
Einsetzen von  in
in  liefert für
liefert für 
![\(\begin{array}[t]{rll}
m&=&f](https://mathjax.schullv.de/1969cc5f1b77826ba2c59366d2ce30451a0181457389fa624bc6f901c35ed0fe?color=5a5a5a) Da die Tangente im Ursprung anliegt, gilt
Da die Tangente im Ursprung anliegt, gilt  Somit folgt
Somit folgt 
1.1.6
1.2
1.2.1
Ein Zeitpunkt, an dem die momentane Änderungsrate minimal ist, ist z.B. um  Uhr.
Uhr.
1.2.2
Da der Graph von  nie unter die
nie unter die  -Achse fällt, ist
-Achse fällt, ist  für alle
für alle  Dies bedeutet, dass die Änderungsrate des Wasservolumens immer positiv oder Null ist, das Volumen also zu keinem Zeitpunkt abnimmt.
Dies bedeutet, dass die Änderungsrate des Wasservolumens immer positiv oder Null ist, das Volumen also zu keinem Zeitpunkt abnimmt.
1.2.3
Zwei Zeitintervalle, in denen die momentane Änderungsrate des Wasservolumens höchstens  beträgt, sind
beträgt, sind  Uhr bis
Uhr bis  Uhr und
Uhr und  Uhr bis
Uhr bis  Uhr.
Uhr.
1.2.4
Das Volumen des Wassers, das in den ersten zwei Stunden in das Wasserbecken einströmt, ist das Integral der Änderungsrate von  bis
bis 
Aus der Abbildung geht hervor, dass das ungefähr 20 Kästchen entspricht. Da 4 Kästchen entspricht, folgt somit eine eingeströmte Wassermenge von
entspricht, folgt somit eine eingeströmte Wassermenge von ![\(5\cdot2=10\;[\text{m}^3].\)](https://mathjax.schullv.de/da0a5a7fd503b859c62b069859b89b90289f9c3113dc862ead51dd5cceacbf04?color=5a5a5a)
Aus der Abbildung geht hervor, dass das ungefähr 20 Kästchen entspricht. Da 4 Kästchen
1.2.5
Da  eine ganzrationale Funktion 3. Grades ist, hat ihre allgemeine Funktionsgleichung die Form
eine ganzrationale Funktion 3. Grades ist, hat ihre allgemeine Funktionsgleichung die Form  Einsetzen des Schnittpunktes mit der
Einsetzen des Schnittpunktes mit der  -Achse liefert:
-Achse liefert:
![\(\begin{array}[t]{rll}
w(0)&=&16 \\[5pt]
a\cdot0^3 + b\cdot0^2 + c\cdot0 + d&=&16 \\[5pt]
d&=&16
\end{array}\)](https://mathjax.schullv.de/104ddc2404d4de093e7c90f5eef064c97f306cafac34383304a6230147071394?color=5a5a5a) Für die ersten beiden Ableitungen von
Für die ersten beiden Ableitungen von  folgt:
folgt:

 Einsetzen der Wendepunktbedingung
Einsetzen der Wendepunktbedingung  liefert:
liefert:
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/a991e0d2449c6ec843510298e9cc1362fc35afd0c987b661cca77c7017305184?color=5a5a5a) Die restlichen beiden Bedingungen liefern
Die restlichen beiden Bedingungen liefern  und
und  Durch Einsetzen von
Durch Einsetzen von  folgt insgesamt:
folgt insgesamt:
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/87d2f906f6df62b2bb4f30c84ffa879cf1973cc236c9193377c279c0e56646eb?color=5a5a5a)
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/24a40e0ed7799399542a971e24f4cc97d4aa2c968e75eeca02cf2e7b895340a1?color=5a5a5a) Abziehen der ersten Gleichung von der zweiten liefert
Abziehen der ersten Gleichung von der zweiten liefert  und damit
und damit  Somit folgt
Somit folgt  und durch Einsetzen von
und durch Einsetzen von  in
in  ergibt sich für
ergibt sich für 
![\(\begin{array}[t]{rll}
-36\cdot\left(-\dfrac{1}{2}\right)+c&=&0 &\quad \scriptsize \mid\;-18\\[5pt]
c&=&-18
\end{array}\)](https://mathjax.schullv.de/e22b56c5948a1618374a4661d3ed2d6653c748c6144d6653f693ce9165209f8d?color=5a5a5a) Einsetzen aller Werte liefert folgende Funktionsgleichung für
Einsetzen aller Werte liefert folgende Funktionsgleichung für 

1.2.6
„Berechne die Anzahl der Stunden nach Beobachtungsbeginn, für die die Menge des zugeflossenen Wassers seit 02:00 Uhr doppelt so groß ist wie die in den ersten zwei Stunden zugeflossenen Menge.“