Wahlteil A2

A2 Analytische Geometrie

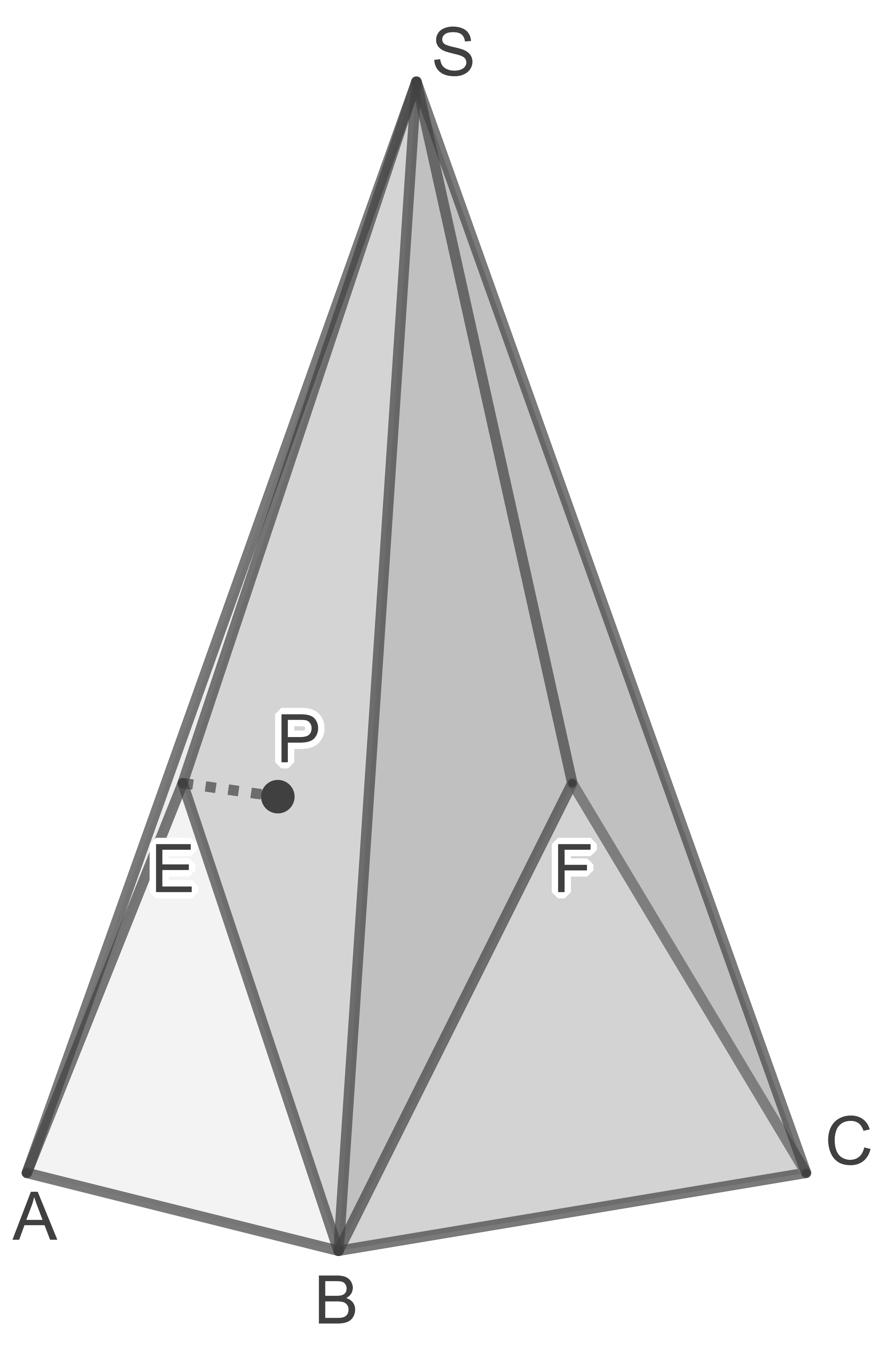
Graphische Darstellung eines vierseitigen Pyramidenmodells mit gekennzeichneten Punkten und Linien.

Abb. 1: Kirchturmspitze

Turm einer Kirche mit roten Dächern und Uhren unter einem bewölkten Himmel.

Abb. 2: Kirchturmspitze

Die Abbildung 1 zeigt ein Modell der Kirchturmspitze in der Abbildung 2.
Im Modell bildet das Quadrat $ABCD$ die Grundfläche des Körpers.
Das Modell ist u. a. symmetrisch zu der Ebene durch die Punkte $A,$ $C$ und $S$ sowie zu der Ebene durch die Punkte $B,$ $D$ und $S.$

Aus dem Modell sind die folgenden Punkte bekannt:
$A(5 \mid -5 \mid 0),$ $B(5 \mid 5 \mid 0),$ $C(-5 \mid 5 \mid 0),$ $S(0 \mid 0 \mid 24)$ und $E(5 \mid 0 \mid 9).$

2.1

Gib die Koordinaten des Punktes $D$ an.

(1 BE)

2.2

Prüfe, ob die folgenden Aussagen wahr oder falsch sind.

Das Dreieck $ABE$ ist gleichschenklig.
Das Dreieck $ABE$ ist rechtwinklig.

(4 BE)

2.3

Bestimme die Koordinaten des Punktes $F.$

(2 BE)

2.4

Gib eine Gleichung für die Gerade $h$ an, die durch die Punkte $E$ und $S$ verläuft.
Berechne die Koordinaten des Schnittpunktes und die Größe des Schnittwinkels von $h$ mit der $x$ -Achse.

(6 BE)

2.5