Pflichtaufgaben

Analysis

Gegeben sind die in $\mathbb{R}$ definierten ganzrationalen Funktionen $f_k$ mit $f_k(x)=x^4+(2-k)\cdot x^3-k\cdot x^2$ und $k\in\mathbb{R}.$

1.1

Begründe, dass der Graph von $f_2$ symmetrisch bezüglich der $y$ -Achse ist.

(1 BE)

1.2

Es gibt einen Wert von $k,$ für den $1$ eine Wendestelle von $f_k$ ist.

Berechne diesen Wert von $k.$

(4 BE)

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f$ mit $f(x)=\cos (x)$ und $g_k$ mit $g_k(x)=k\cdot x^2$ mit $k\in\mathbb{R}^+$ . Die Abbildung zeigt die Graphen von $f$ und $g_{\frac{1}{50}}.$

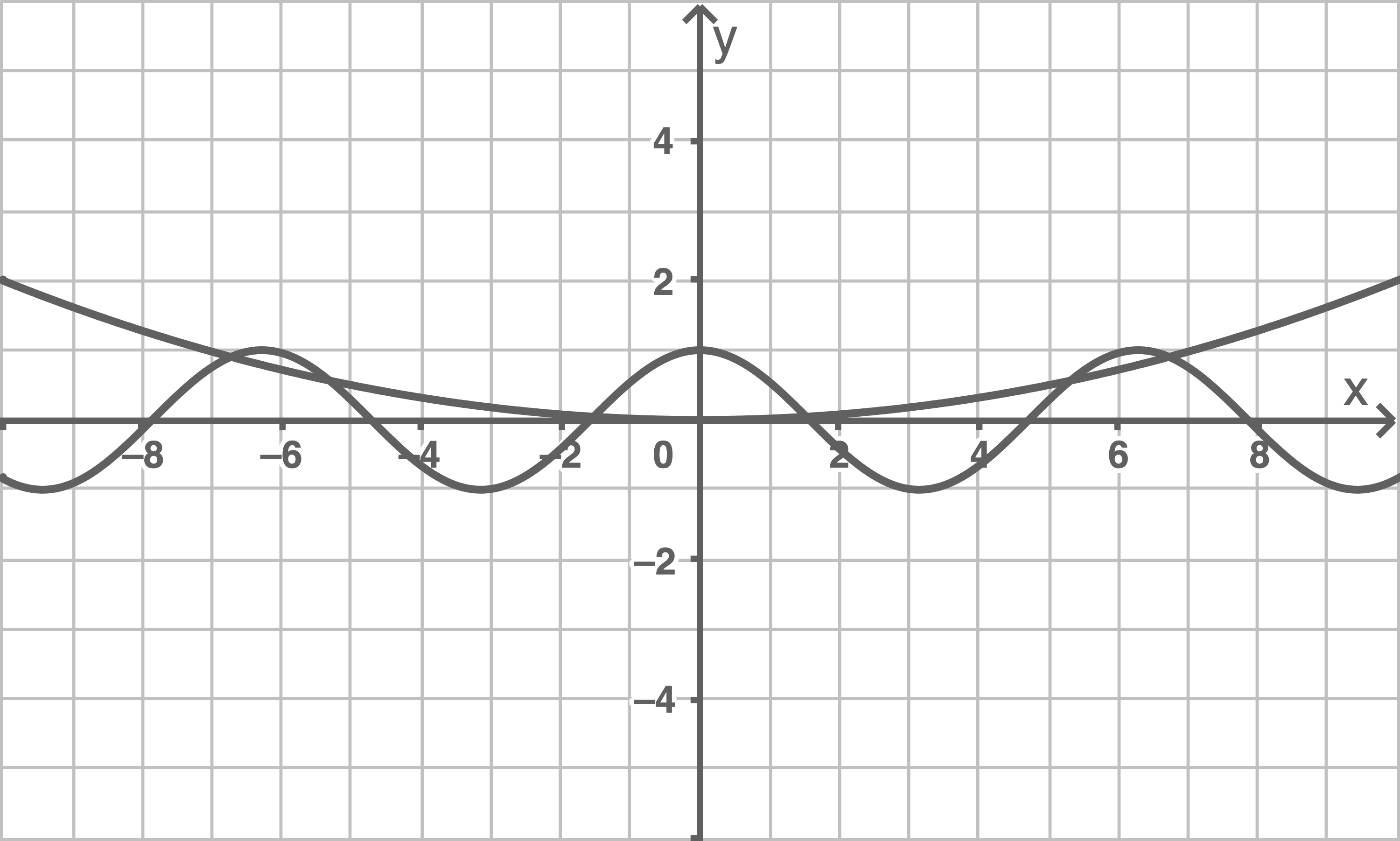
2.1

Skizziere in der Abbildung den Graphen von $g_{\frac{1}{4}}.$

(2 BE)

2.2

Entscheide, ob es Werte von $k$ gibt, für die die Gleichung $f(x)=g_k(x)$ mehr als 2022 Lösungen hat. Begründe deine Entscheidung.

(3 BE)

Analytische Geometrie

Wird der Punkt $P(1\mid 2\mid 3)$ an der Ebene $E$ gespiegelt, so ergibt sich der Punkt $Q(7\mid 2\mid 11).$

3.1

Bestimme eine Gleichung von $E$ in Koordinatenform.

(3 BE)

3.2

Auf der Gerade durch $P$ und $Q$ liegen die Punkte $R$ und $S$ symmetrisch bezüglich $E;$ dabei liegt $R$ bezüglich $E$ auf der gleichen Seite wie $P.$ Der Abstand von $R$ und $S$ ist doppelt so groß wie der Abstand von $P$ und $Q.$

Bestimme die Koordinaten von $R.$

(2 BE)

Stochastik

Gegeben sind die im Folgenden beschriebenen Zufallsgrößen $X$ und $Y:$

Ein Würfel, dessen Seiten mit den Zahlen von 1 bis 6 durchnummeriert sind, wird zweimal geworfen. $X$ gibt die dabei erzielte Augensumme an.
Aus einem Behälter mit 60 schwarzen und 40 weißen Kugeln wird zwölfmal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. $Y$ gibt die Anzahl der entnommenen schwarzen Kugeln an.

4.1

Begründe, dass die Wahrscheinlichkeit $P(X=4)$ mit der Wahrscheinlichkeit $P(X=10)$ übereinstimmt.

(2 BE)

4.2

Die Wahrscheinlichkeitsverteilungen von $X$ und $Y$ werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt.

Ordne $X$ und $Y$ jeweils dem passenden Diagramm zu und begründe deine Zuordnung.

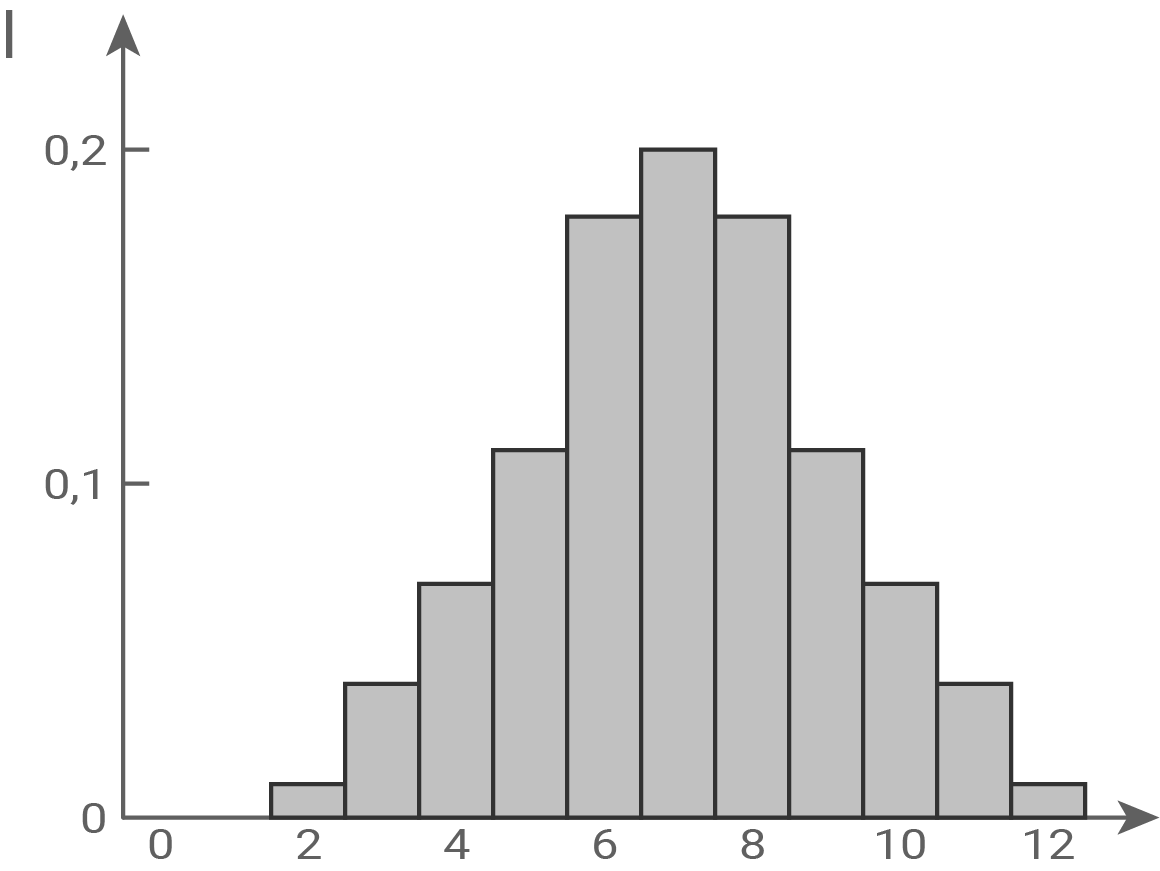
Mecklenburg-Vorpommern Abi 2022 Wahrscheinlichkeitsverteilungen 1

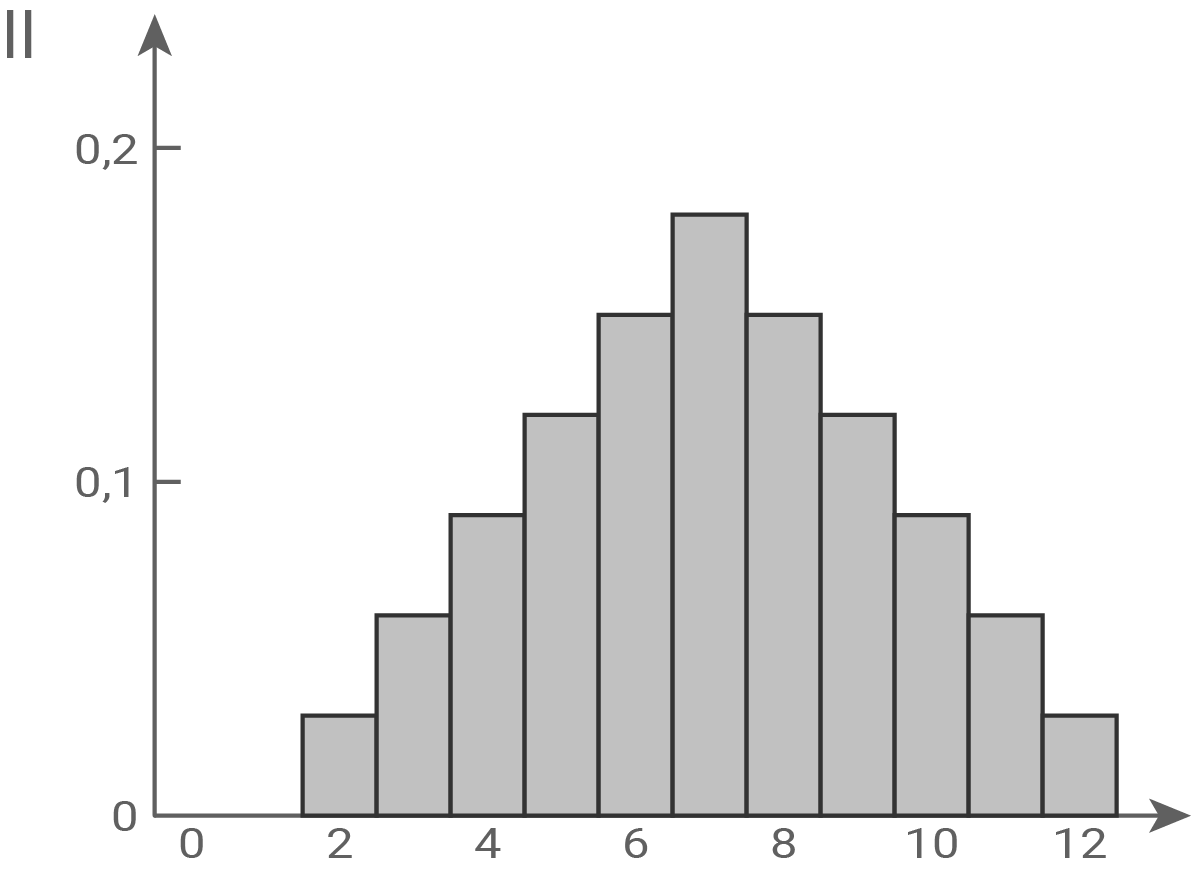
Mecklenburg-Vorpommern Abi 2022 Wahrscheinlichkeitsverteilungen 2

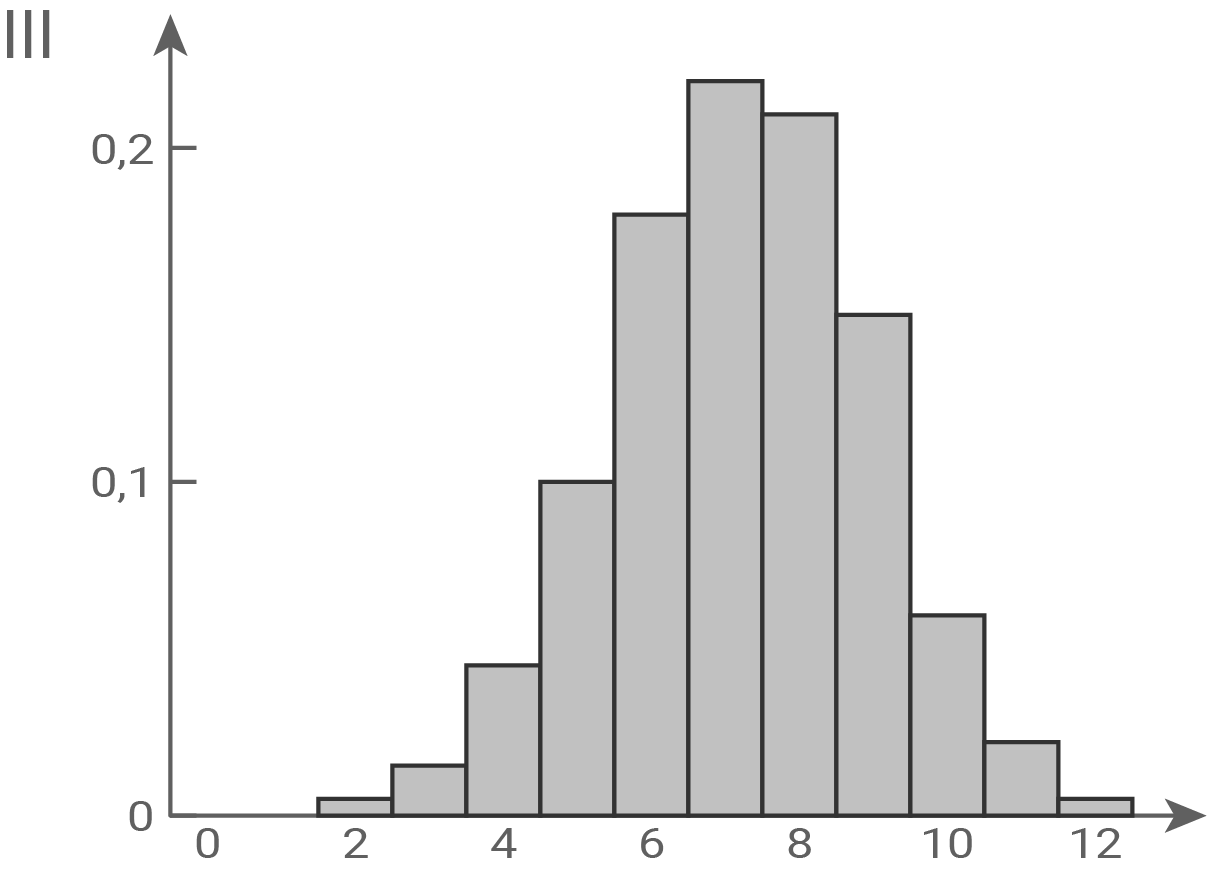
Mecklenburg-Vorpommern Abi 2022 Wahrscheinlichkeitsverteilungen 3

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Für $k=2$ erhält man $f_2(x)=x^4+\underbrace{\left(2-2\right)\cdot x^3}_{=0}-k\cdot x^2$ $=x^4-k\cdot x^2.$

Der Funktionstermin von $f_2$ hat somit nur gerade Exponenten. Also verläuft der Graph von $f_2$ symmetrisch zur $y$ -Achse.

1.2

$\(f_k$ $=4x^3+\left(6-3k\right)\cdot x^2-2k\cdot x$

$\(f_k$ $=12x^2+\left(12-6k\right)\cdot x-2k$

Für die Wendestelle $x=1$ gilt:

$\(\begin{array}[t]{rll} f_k$

Auf die Überprüfung des hinreichenden Kriteriums kann verzichtet werden, da laut Aufgabenstellung nur ein $k$ existiert, für das es eine Wendestelle gibt.

2.1

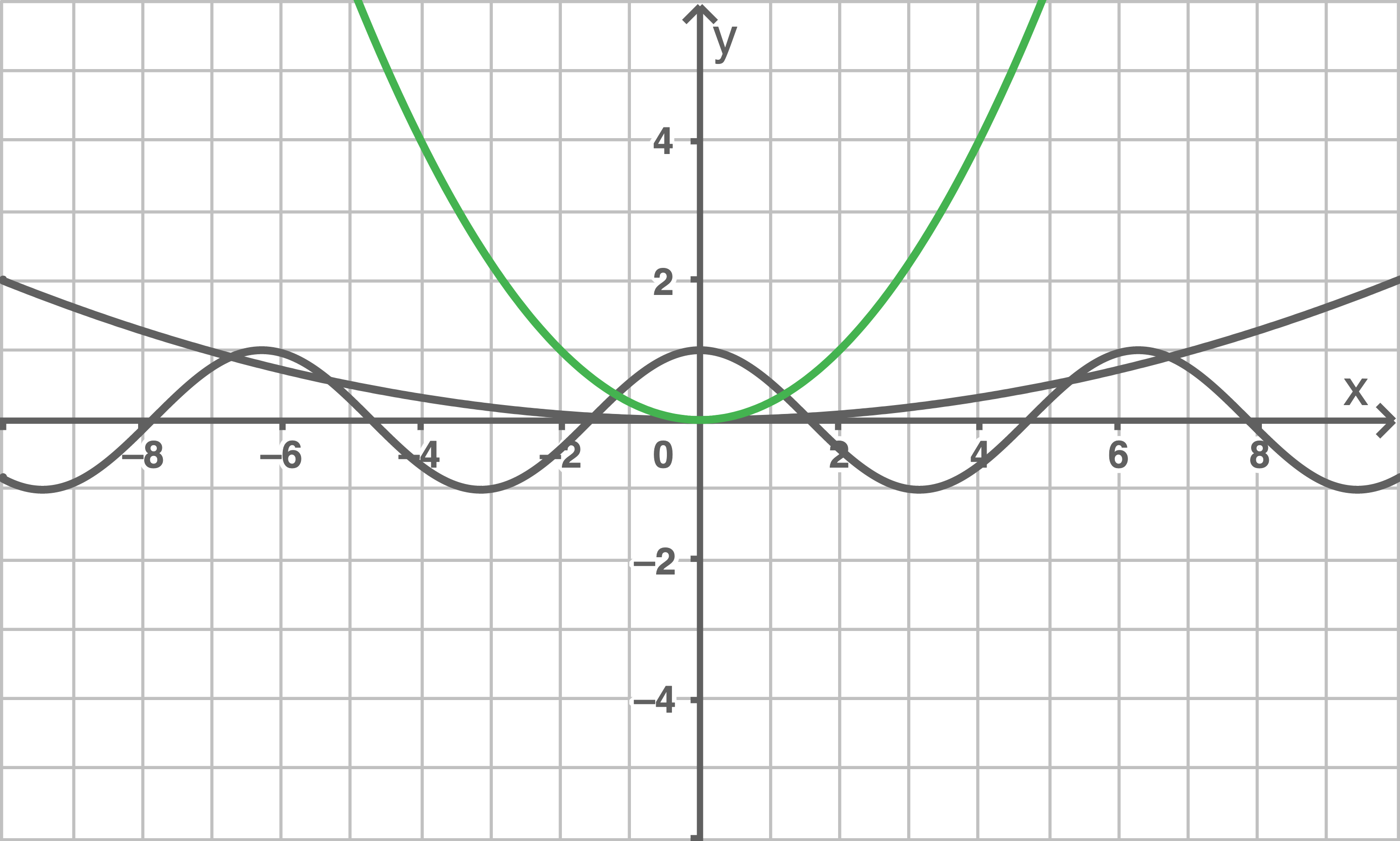
2.2

Die Anzahl der Lösungen der Gleichung $f(x)=g_k(x)$ entspricht der Anzahl der Schnittstellen der beiden Funktionsgraphen von $f$ und $g_k.$

$f$ ist eine periodische Funktion mit dem Wertebereich $-1\leq y\leq 1$ und der Periodenlänge $2\pi.$ Innerhalb jeder Periode kann der Graph von $g_k$ den Graphen von $f$ zwei Mal schneiden.

Je kleiner $k,$ umso mehr gemeinsame Schnittstellen haben die beiden Graphen. Wird $k$ hinreichend klein gewählt, so wird der Graph von $g_k$ genügend stark gestaucht, sodass die Graphen beider Funktionen 2022 Schnittpunkte besitzen können. Somit gibt es Werte $k,$ für die die gegebene Gleichung mehr als 2022 Lösungen hat.

3.1

Der Vektor $\overrightarrow{PQ}=\pmatrix{6\\0\\8}$ steht senkrecht auf der Spiegelebene $E$ und ist somit ein Normalenvektor von $E.$

Die Ebene verläuft durch den Mittelpunkt $M$ der Strecke $\overline{PQ},$ da $P$ und $Q$ symmetrisch zu beiden Seiten der Ebene liegen.

$M\left(\frac{7+1}{2}\mid\frac{2+2}{2}\mid\frac{3+11}{2}\right)$ $=M(4\mid 2\mid 7)$

Mit Hilfe des Normalenvektors und des Punktes $M$ erhält man für die Koordinatengleichung:

$E:6x+0y+8z=d$

$M$ eingesetzt ergibt: $d=6\cdot 4+0\cdot 2+8\cdot 7$ $=80$

Daraus folgt: $E:6x+8z=80$

3.2

Da der Abstand von $R$ und $S$ doppelt so groß ist, wie der Abstand von $P$ und $Q,$ folgt aufgrund der symmetrischen Lage: $\overrightarrow{RP}=\overrightarrow{PM}=\overrightarrow{MQ}=\overrightarrow{QS},$ wobei $M$ der Mittelpunkt der Strecke $\overline{PQ}$ ist.

Da alle Punkte auf einer gemeinsamen Geraden liegen, gilt:

$\overrightarrow{OR}=\overrightarrow{OP}-\frac{1}{2}\cdot\overrightarrow{PQ}$ $=\pmatrix{1\\2\\3}-\frac{1}{2}\cdot\pmatrix{6\\0\\8}$ $=\pmatrix{-2\\2\\-1}$

Daraus folgt: $R(-2\mid 2\mid -1)$

4.1

Beiden Augensummen liegt die gleiche Anzahl an möglichen Ergebnissen mit jeweils der Wahrscheinlichkeit $\frac{1}{36}$ zu Grunde:

$X=4:$ $(1;3),(3;1),(2;2)$

$X=10:$ $(4;6),(6;4),(5;5)$

4.2

Die symmetrische Wahrscheinlichkeitsverteilung von $X$ wird durch Diagramm II dargestellt: Die Wahrscheinlichkeit $P(X=3)=\frac{2}{36}$ ist doppelt so groß wie $P(X=2)=\frac{1}{36}.$ Außerdem sind alle Wahrscheinlichkeiten von $X$ ganzzahlige Vielfache von $\frac{1}{36}$ . Das trifft nur auf Diagramm II zu.

$Y$ ist binomialverteilt mit $p=\frac{3}{5},$ die Wahrscheinlichkeitsverteilung von $Y$ ist nicht symmetrisch und wird durch Abbildung III dargestellt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?