Wahlteil B2
B2 Analytische Geometrie
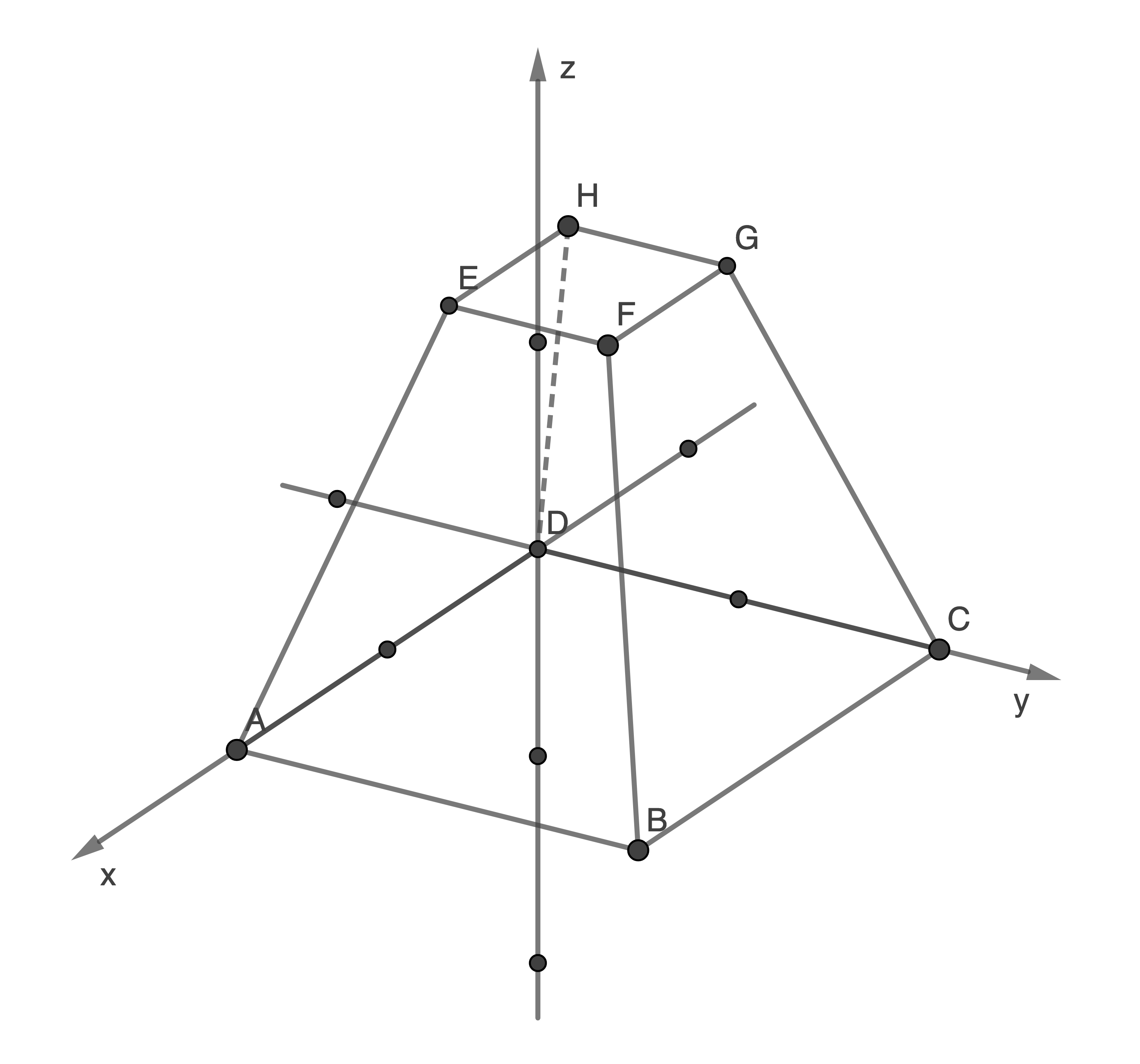
In einem kartesischen Koordinatensystem bilden die Punkte
2.1
Gib die Koordinaten des Punktes  in Abhängigkeit von
in Abhängigkeit von  an.
an.
(1 BE)
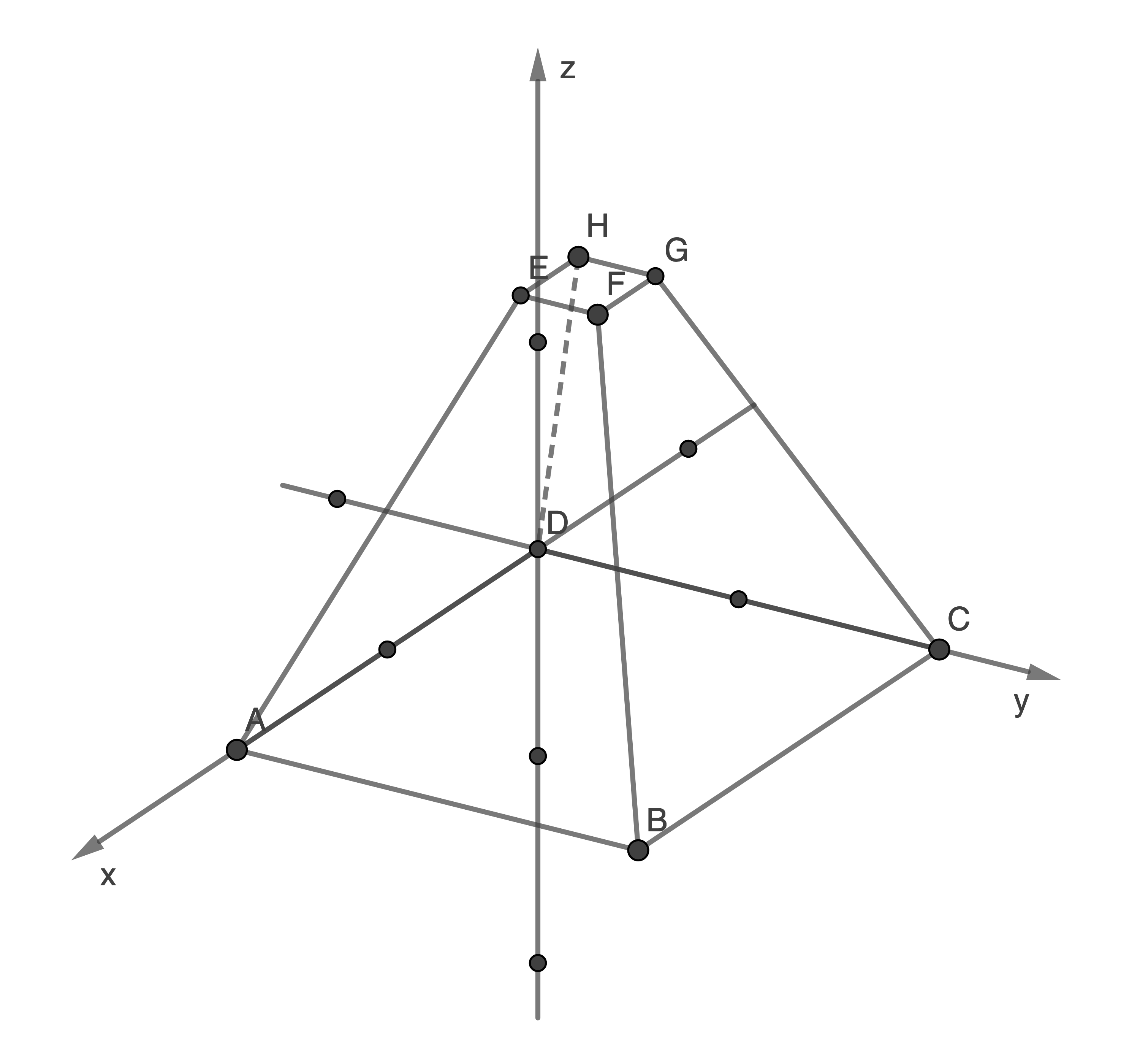
2.2
Stelle  für
für  in einem kartesischen Koordinatensystem dar.
(
in einem kartesischen Koordinatensystem dar.
( Längeneinheit =
Längeneinheit =  )
)
(3 BE)
2.3
Die Kante  schließt mit der Grundfläche
schließt mit der Grundfläche  einen Neigungswinkel ein.
einen Neigungswinkel ein.
2.3.1
Berechne den Neigungswinkel der Kante  zur Grundfläche
zur Grundfläche  .
.
(3 BE)
2.3.2
Zeige, dass es keinen Pyramidenstumpf gibt, sodass dieser Neigungswinkel  beträgt.
beträgt.
(3 BE)
2.4
Berechne den Abstand des Mittelpunktes der Strecke  zur Ebene
zur Ebene  durch die Punkte
durch die Punkte  ,
,  und
und  in Abhängigkeit von
in Abhängigkeit von  .
.
(4 BE)
2.5
Jeder Pyramidenstumpf  ist Teil einer Pyramide
ist Teil einer Pyramide  .
.
Bestimme die Koordinaten des Punktes in Abhängigkeit von
in Abhängigkeit von  .
.
Bestimme die Koordinaten des Punktes
(4 BE)
2.6
Das Volumen des Pyramidenstumpfes  in Abhängigkeit von
in Abhängigkeit von  ist
ist  .
.
Begründe, dass Folgendes gilt: .
.
Begründe, dass Folgendes gilt:
(3 BE)
2.7
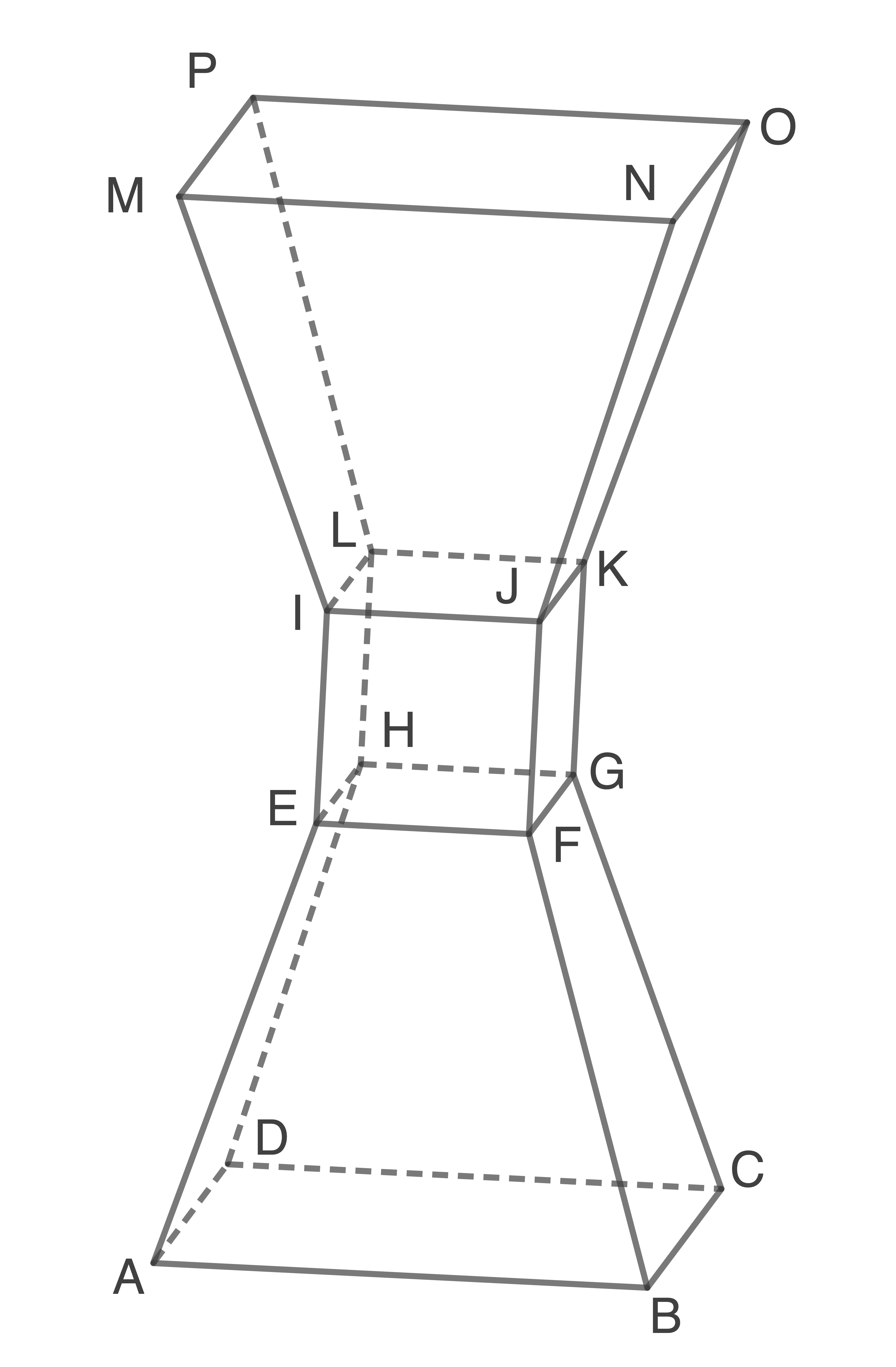
Als Symbol für eine Ausstellung zum Thema „Höchste Zeit für die Rettung der Weltmeere“ wird ein Hohlkörper aus Glas geplant. Dieser Körper wird mit Wasser gefüllt, in dem Plastikmüllteilchen schweben.
Die Abbildung zeigt ein Modell  , das aus zwei kongruenten Pyramidenstümpfen und einem Würfel zusammengesetzt ist. Der untere Pyramidenstumpf ist im Modell der Körper
, das aus zwei kongruenten Pyramidenstümpfen und einem Würfel zusammengesetzt ist. Der untere Pyramidenstumpf ist im Modell der Körper  für einen Wert von
für einen Wert von  .
Eine Längeneinheit entspricht einem Meter.
.
Eine Längeneinheit entspricht einem Meter.
2.7.1
Die Kante  soll in der Realität aus statischen Gründen eine Länge von
soll in der Realität aus statischen Gründen eine Länge von  haben.
haben.
Bestimme für diese Kantenlänge den Wert von .
.
Bestimme für diese Kantenlänge den Wert von
(3 BE)
2.7.2
Der Körper wird nach dem Modell  für
für  gebaut.
gebaut.
Es wird Wasser bis auf eine Höhe von eingefüllt.
eingefüllt.
Bestimme das Volumen des eingefüllten Wassers in Kubikmetern. Hinweis: Die Glaswandstärke wird vernachlässigt.
Es wird Wasser bis auf eine Höhe von
Bestimme das Volumen des eingefüllten Wassers in Kubikmetern. Hinweis: Die Glaswandstärke wird vernachlässigt.
(6 BE)
2.1
2.2
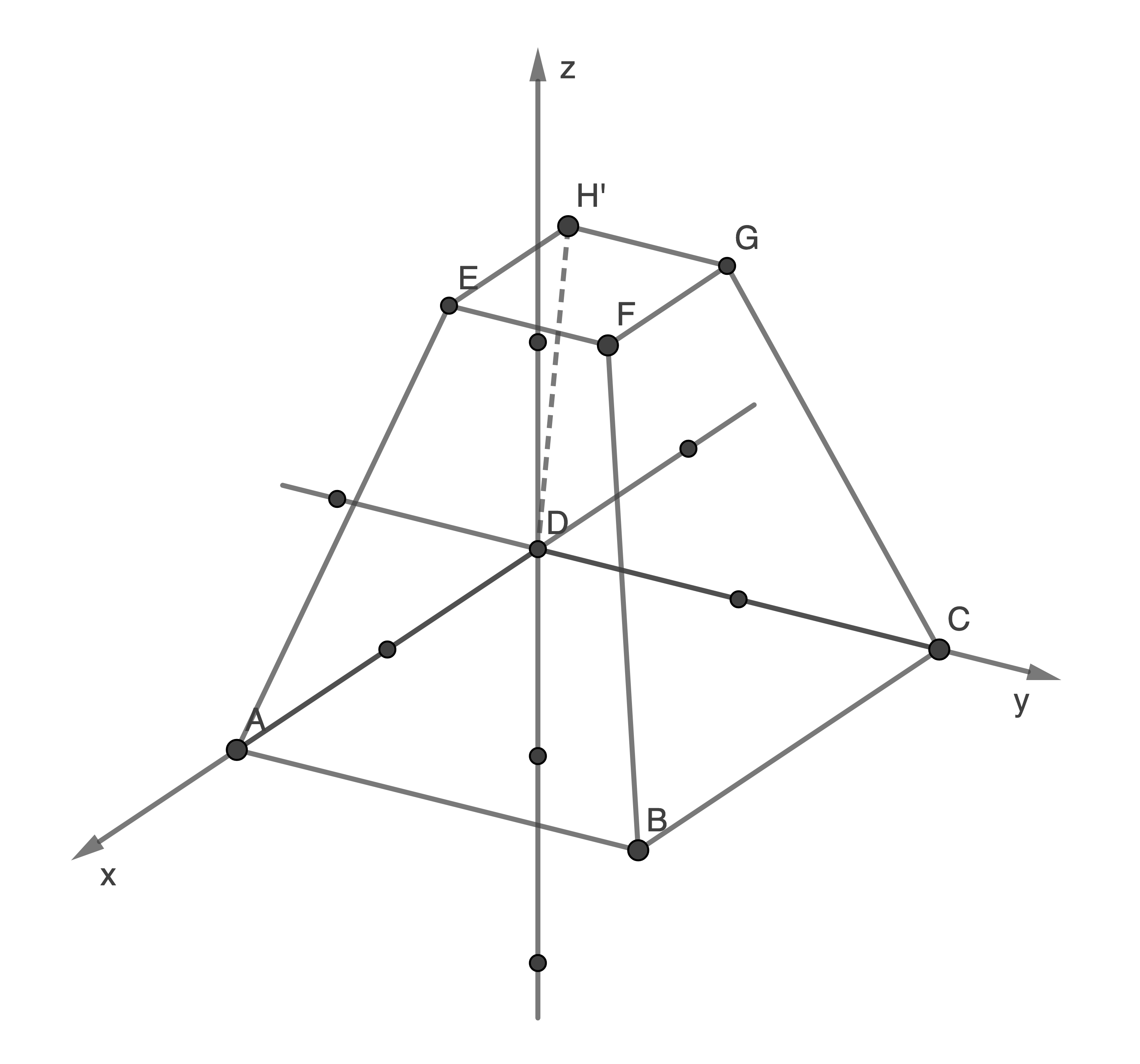 Abbildung nicht maßstäblich.
Abbildung nicht maßstäblich.
2.3.1
Neigungswinkel:
 Normalenvektor der Grundfläche
Normalenvektor der Grundfläche 
![\(\begin{array}[t]{rll}
\sin \alpha&=&\dfrac{\pmatrix{-0,5\\0,5\\2} \circ \pmatrix{0\\0\\1}}{\left|\pmatrix{-0,5\\0,5\\2}\right|} &\quad \\[5pt]
\sin \alpha&=& \dfrac{2\sqrt{2}}{3}&\quad \\[5pt]
\sin \alpha &\approx& 0,9482&\quad \scriptsize \mid\;\arcsin \\[5pt]
\alpha&=&70,5^{\circ} &\quad \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e5c92e862fe3bc4f4c05a0122ad119e0f6fb2bca1fe8261da2a09323b44a5e18?color=5a5a5a)
2.3.2
Nachweis:

![\(\begin{array}[t]{rll}
\dfrac {\sqrt{2}}{2} &=&\dfrac {\pmatrix{-a\\a\\2}\circ \pmatrix{0\\0\\1}}{\pmatrix{-a\\a\\2}} &\quad \scriptsize \mid\;\cdot(2a^2+4) \\[5pt]
\dfrac {\sqrt{2}}{2}\cdot(2a^2+4) &=&2 &\quad \scriptsize \mid\;:\frac{\sqrt2}{2} \\[5pt]
2a^2+4&=&2\sqrt2 &\quad \scriptsize \mid\;-4\mid\;:2 \\[5pt]
a^2&=&-2+\sqrt2\lt0 &\quad \\[5pt]
\end{array}\)](https://mathjax.schullv.de/8f3854b82748f46b7beb87d7dd55d3ecd4d8c6c0008c4c2eac88a002c2657ab8?color=5a5a5a) Da das Ergebnis einer Quadratur nicht negativ sein kann, ist
Da das Ergebnis einer Quadratur nicht negativ sein kann, ist 
2.4
Mittelpunkt von 

 Gleichung der Ebene
Gleichung der Ebene  :
:

![\(\begin{array}[t]{rll}
\overrightarrow{n}\circ\overrightarrow{OA}&=&q &\quad \\[5pt]
8&=& q&\quad \\[5pt]
\end{array}\)](https://mathjax.schullv.de/389c6891ad8a6cc8727619c8317376df75af6d0b9663aa10ce1d7cec9e5f1613?color=5a5a5a)
 Abstand
Abstand  zur Ebene:
zur Ebene:


2.5
Gerader Pyramidenstumpf: Spitze über dem Mittelpunkt  der Grundfläche
der Grundfläche
 Strahlensatz:
Strahlensatz:

![\(\begin{array}[t]{rll}
\dfrac{2}{h_P}&=& \dfrac{2(1-a)}{h_P-2} &\quad \scriptsize \mid\;\cdot h_P\mid\;\cdot(h_p-2) \\[5pt]
2h_P - 4&=& -2ah_P + 2h_P &\quad \scriptsize \mid\;+4\mid\;-2h_P\mid\;+2ah_P \\[5pt]
2ah_P&=& 4 &\quad \scriptsize \mid\;:2a \\[5pt]
h_P &=& \dfrac{2}{a}
\end{array}\)](https://mathjax.schullv.de/d99b664e3fe0154f8e20312f5623898bb3ae9c94123650f1fedaaa1fd5ef433d?color=5a5a5a)
 oder Berechnung Schnittpunkt zweier Geraden:
oder Berechnung Schnittpunkt zweier Geraden:
 und
und 


 Setze
Setze  in
in  ein, um die
ein, um die  Koordinate zu bestimmen.
Koordinate zu bestimmen.

2.6
Begründung:
Für  gilt:
gilt:

 .
Der Grenzkörper ist eine Pyramide mit der Höhe
.
Der Grenzkörper ist eine Pyramide mit der Höhe  .
.
 oder
oder
 mit
mit  und
und 



2.7.1
2.7.2
Gesamthöhe des Modells für 

 Gesamtvolumen des Modells:
Gesamtvolumen des Modells:

 Höhe des nicht gefüllten oberen Pyramidenstumpfes
Höhe des nicht gefüllten oberen Pyramidenstumpfes  :
:
 Also: bis zur Hälfte der Höhe
Also: bis zur Hälfte der Höhe  gefüllt.
Länge der unteren Kante von
gefüllt.
Länge der unteren Kante von  :
:
 Volumen des nicht gefüllten Stumpfes:
Volumen des nicht gefüllten Stumpfes:

 Wasservolumen:
Wasservolumen: