1 Analysis
1.1
Gegeben ist die Funktionenschar  mit
mit 

 Die Graphen von
Die Graphen von  sind
sind  .
.
1.1.1
Gib die Nullstellen von  an.
an.
(2 BE)
1.1.2
Für alle Werte von  hat
hat  zwei Extremstellen.
Weis nach, dass
zwei Extremstellen.
Weis nach, dass  die 1. Ableitungsfunktion von
die 1. Ableitungsfunktion von  ist.
Zeige, dass
ist.
Zeige, dass  und
und  die Extremstellen von
die Extremstellen von  sind.
sind.
(5 BE)
1.1.3
In Abbildung 1 ist der Graph von  dargestellt. Zeichne
dargestellt. Zeichne  in dieses Koordinatensystem.
in dieses Koordinatensystem.
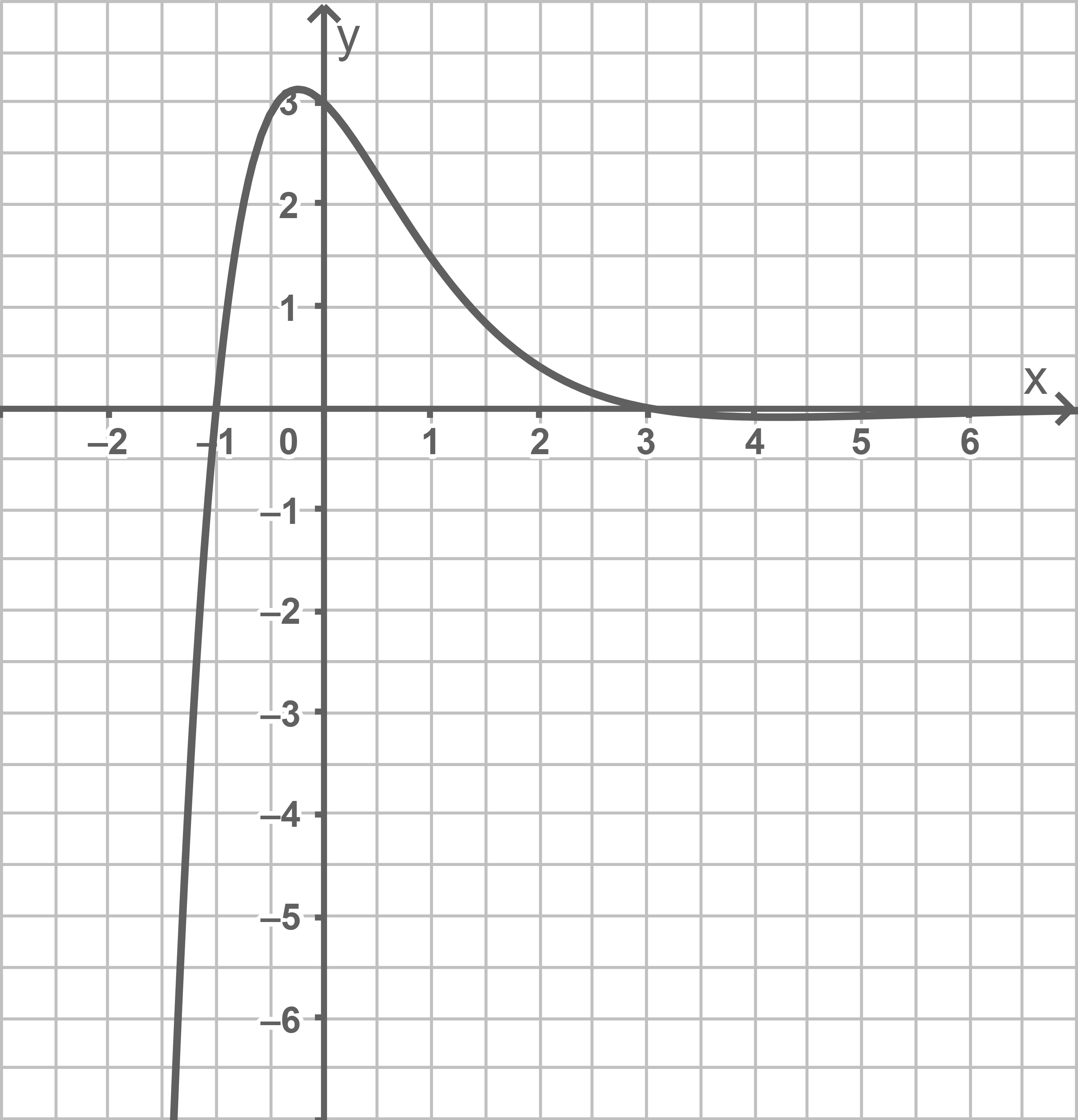

Abbildung 1
(3 BE)
1.1.4
Für einen Wert von  schneiden sich
schneiden sich  und der Graph von
und der Graph von  zweimal so, dass die Schnittstellen einen Abstand von
zweimal so, dass die Schnittstellen einen Abstand von  zueinander haben.
zueinander haben.
Berechne den Wert von
Berechne den Wert von
(5 BE)
1.2
Im Rahmen der Untersuchung eines Patienten werden seine Blutzuckerwerte  in
in  gemessen.
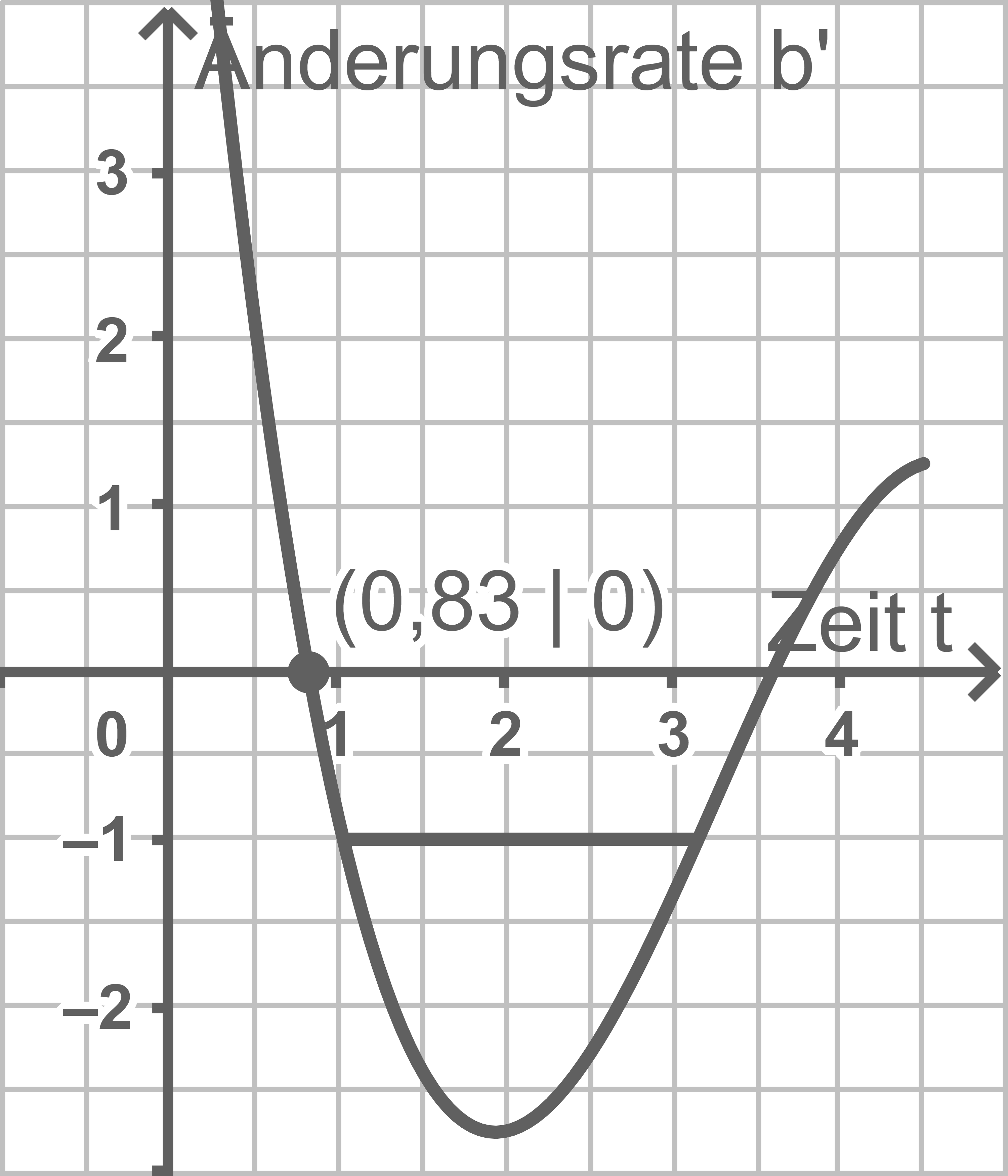
Der Graph in der Abbildung 2 stellt die momentane Änderungsrate
gemessen.
Der Graph in der Abbildung 2 stellt die momentane Änderungsrate  dieser Messwerte in Abhängigkeit von der Zeit
dieser Messwerte in Abhängigkeit von der Zeit  für den Zeitraum
für den Zeitraum  dar. Dabei wird
dar. Dabei wird  in Stunden angegeben.
Zu Messbeginn hat der Patient einen Blutzuckerwert
in Stunden angegeben.
Zu Messbeginn hat der Patient einen Blutzuckerwert 
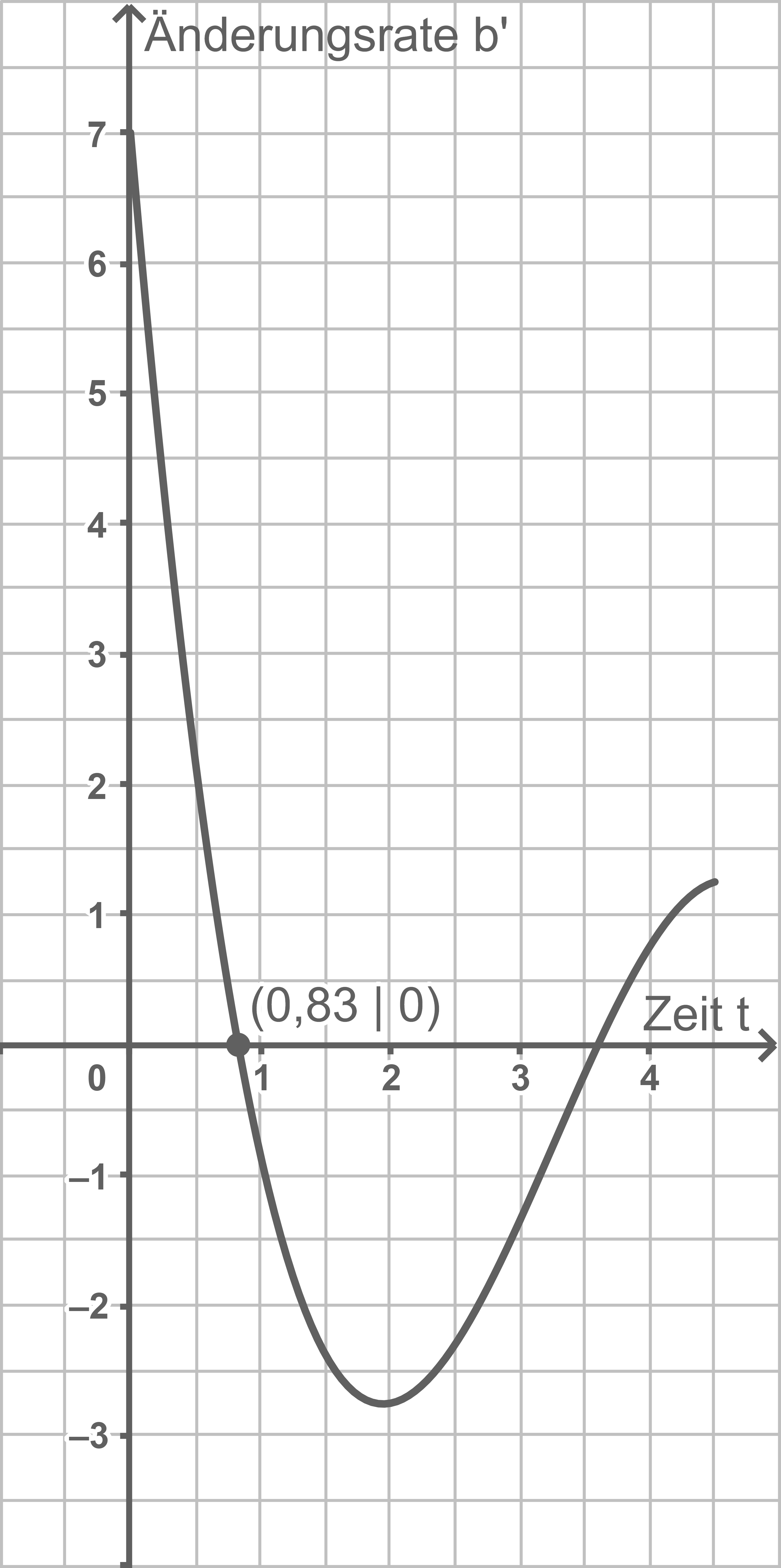
Abbildung 2
1.2.1
Beschreibe mithilfe des Graphen aus Abbildung 2 den Verlauf der Blutzuckerwerte für den oben angegebenen Zeitraum; gehe dabei auch auf die Bedeutung des Tiefpunktes ein.
(5 BE)
1.2.2
Gib die Bedeutung des Terms  im Sachzusammenhang an.
im Sachzusammenhang an.
(2 BE)
1.2.3
Beurteile die folgende Aussage:
Der Betrag der Abweichung des maximalen Blutzuckerwertes vom Ausgangswert  ist größer als der Betrag der Abweichung des minimalen Blutzuckerwertes von
ist größer als der Betrag der Abweichung des minimalen Blutzuckerwertes von 
(4 BE)
1.2.4
Interpretiere die Gleichung  im Sachzusammenhang und gib den Zeitpunkt
im Sachzusammenhang und gib den Zeitpunkt  mithilfe der Abbildung 1 an.
mithilfe der Abbildung 1 an.
(3 BE)
1.3
Durch die Gleichung  ist die in
ist die in  definierte Funktion
definierte Funktion  gegeben (vgl. Abbildung 3). Die Punkte
gegeben (vgl. Abbildung 3). Die Punkte  und
und  sind Eckpunkte des Vierecks
sind Eckpunkte des Vierecks 
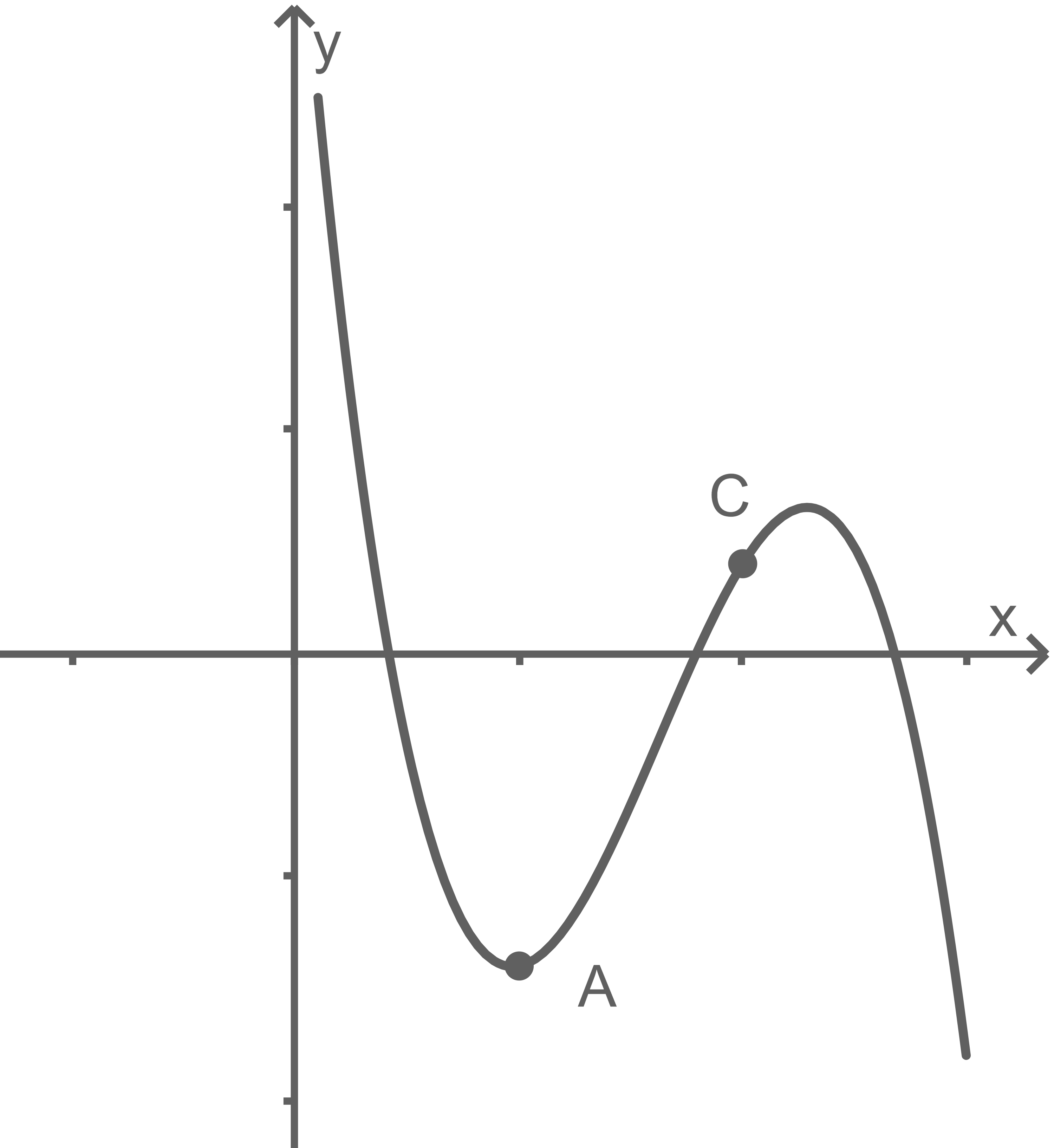
Abbildung 3
1.3.1
Die Punkte  und
und  liegen so, dass
liegen so, dass  ein Quadrat ist. Skizziere dieses Quadrat in Abbildung 3.
ein Quadrat ist. Skizziere dieses Quadrat in Abbildung 3.
(2 BE)
1.3.2
Berechne für das Quadrat  die
die  -Koordinate von
-Koordinate von 
(7 BE)
1.3.3
Die Punkte  und
und  mit
mit  bilden gemeinsam mit
bilden gemeinsam mit  und
und  die Eckpunkte der Drachenvierecke
die Eckpunkte der Drachenvierecke  bei denen die Seiten
bei denen die Seiten  und
und  gleich lang sind. Weiterhin besitzen diese Drachenvierecke rechte Winkel in den Punkten
gleich lang sind. Weiterhin besitzen diese Drachenvierecke rechte Winkel in den Punkten  und
und  Beschreibe die Lage dieser Punkte
Beschreibe die Lage dieser Punkte  und
und 
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1.1
1.1.2
Ableitungsfunktion nachweisen
Mit der Produktregel folgt:
![\(\begin{array}[t]{rll}
f_a(x) &=& \left(x^2-a\right) \cdot \mathrm e^{-x}\\[5pt]
f_a](https://mathjax.schullv.de/cac9cb361e1d935810e581bb9c7e8f0e12ff33bb327d89c9c7d45588597dfb36?color=5a5a5a) Extremstellen zeigen
Um die notwendige Bedingung für Extremstellen zu überprüfen, werden die
Extremstellen zeigen
Um die notwendige Bedingung für Extremstellen zu überprüfen, werden die  -Koordinaten in die erste Ableitungsfunktion eingesetzt:
-Koordinaten in die erste Ableitungsfunktion eingesetzt:
 in
in  einsetzen:
einsetzen:
 in
in  einsetzen:
einsetzen:
1.1.3
1.1.4
Schnittstellen von  und
und  berechnen:
Abstand der Schnittstellen gleich
berechnen:
Abstand der Schnittstellen gleich  setzen und nach
setzen und nach  auflösen:
auflösen:
1.2.1
Der Blutzuckerwert steigt an und erreicht zum Zeitpunkt  Stunden sein Maximum. Danach nimmt der Blutzuckerwert wieder ab und erreicht zum Zeitpunkt
Stunden sein Maximum. Danach nimmt der Blutzuckerwert wieder ab und erreicht zum Zeitpunkt  Stunden nach Beobachtungsbeginn sein Minimum. Danach steigt der Wert wieder an.
Stunden nach Beobachtungsbeginn sein Minimum. Danach steigt der Wert wieder an.  Stunden nach Messbeginn (der Graph hat an dieser Stelle seinen Tiefpunkt) nimmt der Blutzuckerwert am stärksten ab.
Stunden nach Messbeginn (der Graph hat an dieser Stelle seinen Tiefpunkt) nimmt der Blutzuckerwert am stärksten ab.
1.2.2
Der Term  berechnet näherungsweise den Inhalt der Fläche zwischen dem Graph und der
berechnet näherungsweise den Inhalt der Fläche zwischen dem Graph und der  -Achse im Bereich zwischen
-Achse im Bereich zwischen  und
und  Somit wird also die Zunahme des Blutzuckerwertes in
Somit wird also die Zunahme des Blutzuckerwertes in  innerhalb der ersten
innerhalb der ersten  Stunden näherungsweise berechnet.
Stunden näherungsweise berechnet.
1.2.3
Der Betrag der Differenz vom maximalen Blutzuckerwert und  entspricht dem Inhalt der Fläche, die vom Graphen in der Abbildung und den Koordinatenachsen eingeschlossen wird. Der Betrag der Differenz vom minimalen Blutzuckerwert und
entspricht dem Inhalt der Fläche, die vom Graphen in der Abbildung und den Koordinatenachsen eingeschlossen wird. Der Betrag der Differenz vom minimalen Blutzuckerwert und  entspricht dem Betrag des bestimmten Integrals der Funktion im Intervall
entspricht dem Betrag des bestimmten Integrals der Funktion im Intervall ![\([0 ; 3,6]\)](https://mathjax.schullv.de/5b75c4af66061184b3ee058f702a543019768067b0f429b20116157db6480392?color=5a5a5a) beziehungsweise dem Inhalt der Fläche, die der Graph mit der
beziehungsweise dem Inhalt der Fläche, die der Graph mit der  -Achse im IV. Quadranten einschließt, verringert um den Wert von ca.
-Achse im IV. Quadranten einschließt, verringert um den Wert von ca.  Dieser Wert ist kleiner als
Dieser Wert ist kleiner als  Die Aussage ist wahr.
Die Aussage ist wahr.
1.2.4
Die Gleichung gibt an, dass die momentane Änderungsrate zum Zeitpunkt  gleich der momentanen Änderungsrate
gleich der momentanen Änderungsrate  Stunden später ist. Mithilfe der Abbildung lässt sich
Stunden später ist. Mithilfe der Abbildung lässt sich  bestimmen.
bestimmen.
1.3.1
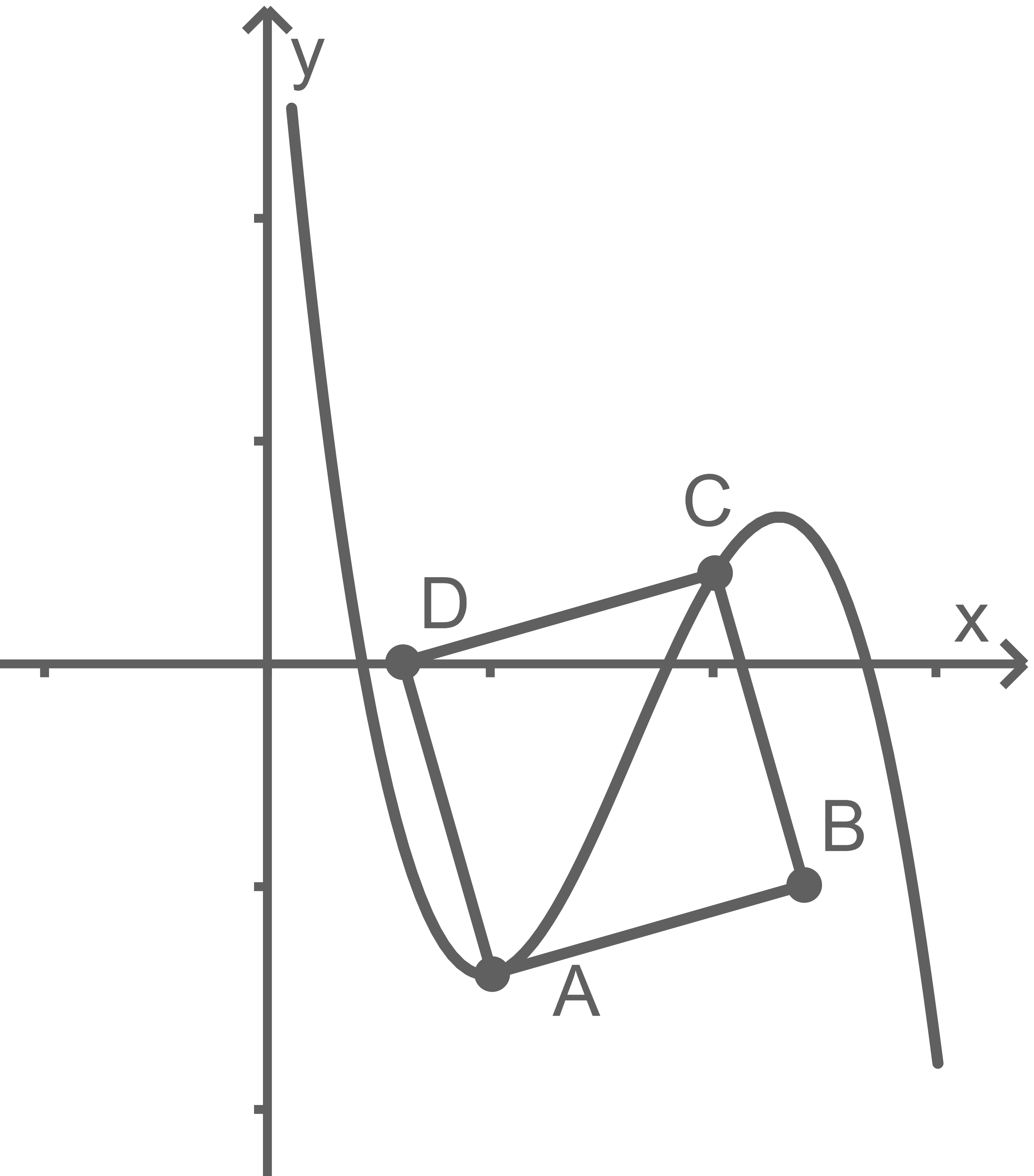
1.3.2
Koordinaten der Punkte  und
und  berechnen:
berechnen:





 Koordinaten des Mittelpunktes
Koordinaten des Mittelpunktes  von
von  bestimmen:
bestimmen:


 Steigung der Gerade durch die Punkte
Steigung der Gerade durch die Punkte  und
und  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
m_{AC} &=& \dfrac{\dfrac{4}{5}-\left(-\dfrac{14}{5}\right)}{4-2} &\\[5pt]
&=&\dfrac{\dfrac{18}{5}}{2} \\[5pt]
&=& \dfrac{18}{5}\cdot \dfrac{1}{2} \\[5pt]
&=& \dfrac{9}{5}
\end{array}\)](https://mathjax.schullv.de/4f8407a95404a10950403e3afa9354c070df2403c4889ec3efbf6e789187434b?color=5a5a5a) Da die Strecke
Da die Strecke  im rechten Winkel zur Strecke
im rechten Winkel zur Strecke  sein muss, ist die Steigung der Gerade durch die Punkte
sein muss, ist die Steigung der Gerade durch die Punkte  und
und  gegeben durch
gegeben durch 
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
-1 &=& - \dfrac{5}{9} \cdot 3 +c \\[5pt]
-1 &=& -\dfrac{5}{3} +c &\quad \scriptsize \mid\; +\dfrac{5}{3} \\[5pt]
\dfrac{2}{3} &=& c
\end{array}\)](https://mathjax.schullv.de/970624dc746712e36a9c07108fb317ba46850ac918189c6e62381c21b5d3ab9e?color=5a5a5a) Ein allgemeiner Punkt
Ein allgemeiner Punkt  der auf der Gerade durch die Punkte
der auf der Gerade durch die Punkte  und
und  liegt, hat also die Koordinaten
liegt, hat also die Koordinaten  Länge der Strecke
Länge der Strecke  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
\mid \overline{AM_{AC}}\mid &=& \sqrt{(3-2)^2+\left(-1+\dfrac{14}{5}\right)^2} \\[5pt]
&=& \sqrt{\dfrac{106}{25}}
\end{array}\)](https://mathjax.schullv.de/dcd24b4a6c6ad2c3744ca61eaf2b5315c74650900b1ddec37f71d10b448000c0?color=5a5a5a) Punkte auf der Gerade durch die Punkte
Punkte auf der Gerade durch die Punkte  und
und  bestimmen, die den selben Abstand zum Punkt
bestimmen, die den selben Abstand zum Punkt  haben wie der Punkt
haben wie der Punkt  Da die
Da die  -Koordinate des Punkts
-Koordinate des Punkts  größer sein muss als die des Punkts
größer sein muss als die des Punkts  muss
muss  die gesuchte
die gesuchte  -Koordinate von
-Koordinate von  sein.
sein.
1.3.3
Die Punkte  und
und  liegen auf dem Kreis um den Punkt
liegen auf dem Kreis um den Punkt  mit dem Radius
mit dem Radius 