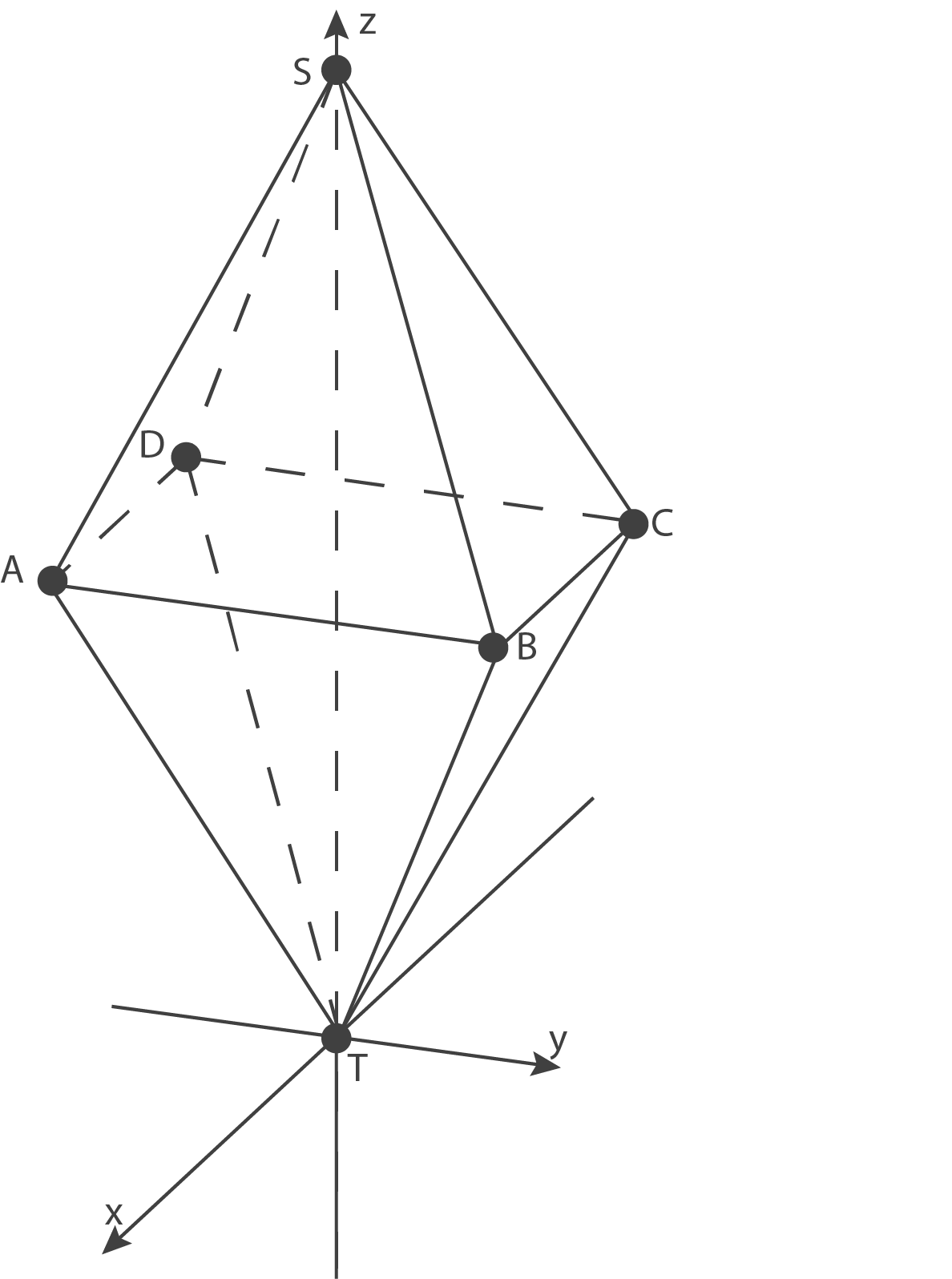
Analytische Geometrie

Gegeben sind die Punkte $A\left(5\mid-5\mid12\right)$ , $B\left(5\mid5\mid12\right)$ und $C\left(-5\mid5\mid12\right)$ .

2.1

Zeige, dass das Dreieck $ABC$ gleichschenklig ist.

(2 BE)

2.2

Begründe, dass $A$ , $B$ und $C$ Eckpunkte eines Quadrats sein können, und gib die Koordinaten des vierten Eckpunkts $D$ dieses Quadrats an.

(3 BE)

Im Folgenden wird die abgebildete Doppelpyramide betrachtet. Die beiden Teilpyramiden $ABCDS$ und $ABCDT$ sind gleich hoch. Der Punkt $T$ liegt im Koordinatenursprung, der Punkt $S$ ebenfalls auf der $z$ -Achse.
Die Seitenfläche $BCT$ liegt in einer Ebene $E$ .

Diagramm eines geometrischen Körpers mit Punkten und Achsen in einem dreidimensionalen Raum.

2.3

Bestimme eine Gleichung von $E$ in Koordinatenform.
(zur Kontrolle: $12y-5z=0$ )

(3 BE)

2.4

Bestimme die Größe des Winkels, den die Seitenfläche $BCT$ mit der Fläche $ABCD$ einschließt.

(3 BE)

2.5

$E$ gehört zur Schar der Ebenen $E_k: k \cdot y-5z=5k-60$ mit $k \in \mathbb{R}$ .

2.5.1

Alle Ebenen der Schar schneiden sich in einer Gerade. Weise nach, dass die Kante $\overline{BC}$ auf dieser Gerade liegt.

(2 BE)

2.5.2

Ermittle diejenigen Werte von $k$ , für die $E_k$ mit der Seitenfläche $ADS$ mindestens einen Punkt gemeinsam hat.

(4 BE)

2.5.3

Die Seitenfläche $ADT$ liegt in der Ebene $F$ .

Gib einen Normalenvektor von $F$ an und begründe deine Angabe, ohne die Koordinaten von $A$ und $D$ zu verwenden. Bestimme denjenigen Wert von $k$ , für den $E_k$ senkrecht zu $F$ steht.

(4 BE)

2.6

Die Doppelpyramide wird so um die $x$ -Achse gedreht, dass die bisher mit $BCT$ bezeichnete Seitenfläche in der $xy$ -Ebene liegt und der bisher mit $S$ bezeichnete Punkt eine positive $y$ -Koordinate hat.
Bestimme diese $y$ -Koordinate und veranschauliche dein Vorgehen durch eine Skizze.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Ein Dreieck ist gleichschenklig, wenn zwei Seiten des Dreiecks gleich lang sind. Hier gilt:

$\left| \overrightarrow{AB} \right| = \left| \pmatrix{0 \\ 10 \\0} \right| = \sqrt{0^2+ 10^2 +0^2}$ $= 10$

$\left| \overrightarrow{BC} \right| = \left| \pmatrix{-10 \\ 0 \\0} \right| = \sqrt{(-10)^2+ 0^2 +0^2}$ $= 10$

Da die Vektoren gleich lang sind, handelt es sich um ein gleichschenkliges Dreieick.

2.2

Wenn das Skalarprodukt zweier Vektoren gleich $0$ ist, bilden sie einen rechten Winkel.

$\overrightarrow{AB} \circ \overrightarrow{BC} = \pmatrix{0 \\ 10 \\0} \circ \pmatrix{-10 \\ 0 \\0}$ $= 0 \cdot (-10) + 10 \cdot 0+ 0\cdot 0$ $= 0$

Damit bilden die Vektoren einen rechten Winkel. Da die Vektoren zudem noch gleich lang sind (siehe Aufgabe $2.1$ ), können die Punkte $A$ , $B$ und $C$ die Eckpunkte eines Quadrats sein.

Der Punkt $D$ entspricht dem um den Vektor $\overrightarrow{BC}$ verschobenen Punkt $A$ . Der Punkt $A\left(5\mid -5\mid 12\right)$ muss also um $-10$ entlang der $x$ -Achse verschoben werden. Damit ergibt sich $D\left(-5\mid-5\mid12\right)$ .

2.3

1. Schritt: Normalenvektor der Ebene bestimmen
Durch das Kreuzprodukt der beiden Richtungsvektoren $\overrightarrow{CB}$ und $\overrightarrow{TB}$ lässt sich ein Normalenvektor der Ebene bestimmen:

$\overrightarrow{BC} \times \overrightarrow{BT} = \pmatrix{-5 -5 \\ 5 -5 \\ 12 - 12} \times \pmatrix{0 - 5 \\ 0 - 5 \\ 0 - 12}$ $= \pmatrix{-10 \\ 0 \\ 0} \times \pmatrix{-5 \\ -5 \\ -12}$ $= \pmatrix{0 \\ 12 \\ 5}$

2. Schritt: Koordinatenform bestimmen

$\begin{array}[t]{rll} 0 \cdot x + 12 \cdot y + 5 \cdot z &=& a&\quad \scriptsize \mid\; T \text{ einsetzen}\\[5pt] 0 \cdot 0 + 12 \cdot 0 + 5 \cdot 0&=& a \\[5pt] 0 & =& a \end{array}$

Damit folgt die Koordinatenform:

$12 \cdot y + 5 \cdot z = 0$

2.4

Der Winkel der beiden Ebenen entspricht gerade dem Winkel zwischen $\overrightarrow{BT}$ und $\overrightarrow{BA}$ . Dieser lässt sich wie folgt berechnen:

Vollständigen Rechenweg anzeigen

$\alpha \approx 67,4°$

Damit beträgt der gesuchte Winkel etwa $67,4°.$

2.5

2.5.1

Damit die Kante $\overline{BC}$ auf der Schnittgeraden der Ebenenschar liegt, müssen die Punkte $C$ und $B$ in jeder Ebene $E_k$ liegen. Dies wird durch Einsetzen in die Koordinatengleichung überprüft:

$\begin{array}[t]{rll} k \cdot y -5z& = & 5k-60 & \quad \scriptsize \mid \; \text{B einsetzen}\\[5pt] k \cdot 5 -5\cdot 12 &=& 5k-60 & \quad \scriptsize \\[5pt] 5k -60 &=& 5k-60 & \quad \scriptsize \\[5pt] \end{array}$

$\begin{array}[t]{rll} k \cdot y -5z&=& 5k-60 & \quad \scriptsize \mid \; \text{C einsetzen}\\[5pt] k \cdot 5 -5\cdot 12 &=& 5k-60 & \quad \scriptsize \\[5pt] 5k -60 &=& 5k-60 & \quad \scriptsize \\[5pt] \end{array}$

Damit liegt die Kante $\overline{BC}$ auf der Schnittgeraden der Ebenenschar $E_k.$

2.5.2

Wenn sich alle Ebenen einer Ebenenschar in einer Geraden schneiden, dann rotiert die Ebenenschar gerade um diese Gerade. In disem Fall ist also die Kante $\overline{BC}$ die Rotationsachse der Ebenenschar. Um nun die gesuchten $k$ zu finden, muss man die Punkte $S$ und $A$ einsetzen. Das Intervall zwischen den beiden zugehörigen $k$ ist dann genau der gesuchte Bereich.

Hier klicken: S einsetzen

$k = -12$

Hier klicken: A einsetzen

$k = 0$

Damit ist der gesuchte Bereich gegeben durch: $-12\leq k\leq0.$

2.5.3

1. Schritt: Normalenvektor von $F$ bestimmen
Für die Berechnung des Normalenvektors von $F$ lässt sich die Symmetrie der Doppelpyramide bezüglich der $xz$ -Ebene ausnutzen. Demnach entspricht die Ebene $F$ gerade der an der $xz$ -Ebene gespiegelten Ebene $E$ . Daraus folgt, dass auch der Normalenvektor von $F$ gerade dem an der $xz$ -Ebene gespiegelten Normalenvektor der Ebene $E$ entspricht. Dann folgt:

Der Normalenvektor von $E$ ergibt sich aus der Koordinatengleichung von $E$ : $\, \overrightarrow{n_E}=\pmatrix{0\\12\\-5}$
Somit lautet der Normalenvektor von $F$ $\, \vec{n_F}=\pmatrix{0\\-12\\-5}$ .

2. Schritt: Das gesuchte $k$ bestimmen
Zwei Ebenen stehen senkrecht zueinander, wenn die jeweiligen Normalenvektoren senkrecht zueinander stehen. $E_k$ steht also senkrecht zu $F$ wenn folgendes gilt:

$\begin{array}[t]{rll} \overrightarrow{n_{E_k}} \circ \overrightarrow{n_F}&=& 0&\quad \scriptsize \\[5pt] \pmatrix{0 \\ k \\ -5} \circ \pmatrix{0 \\ 12 \\ -5}&=& 0& \quad \scriptsize \\[5pt] 12k + 25& =& 0& \quad \scriptsize \mid \; -25 \\[5pt] 12k & = & 25& \quad \scriptsize :12 \\[5pt] k& =& \dfrac{25}{12} \end{array}$

Für $k = \frac{25}{12}$ steht $E_k$ senkrecht zu $F.$

2.6

Die folgende Abbildung zeigt einen Teil des Doppelkegels, bezüglich der $y$ - und $z$ -Achse. Die grünen Strecken sind Kanten des Doppelkegels, die anderen Strecken sind Hilfsstrecken.

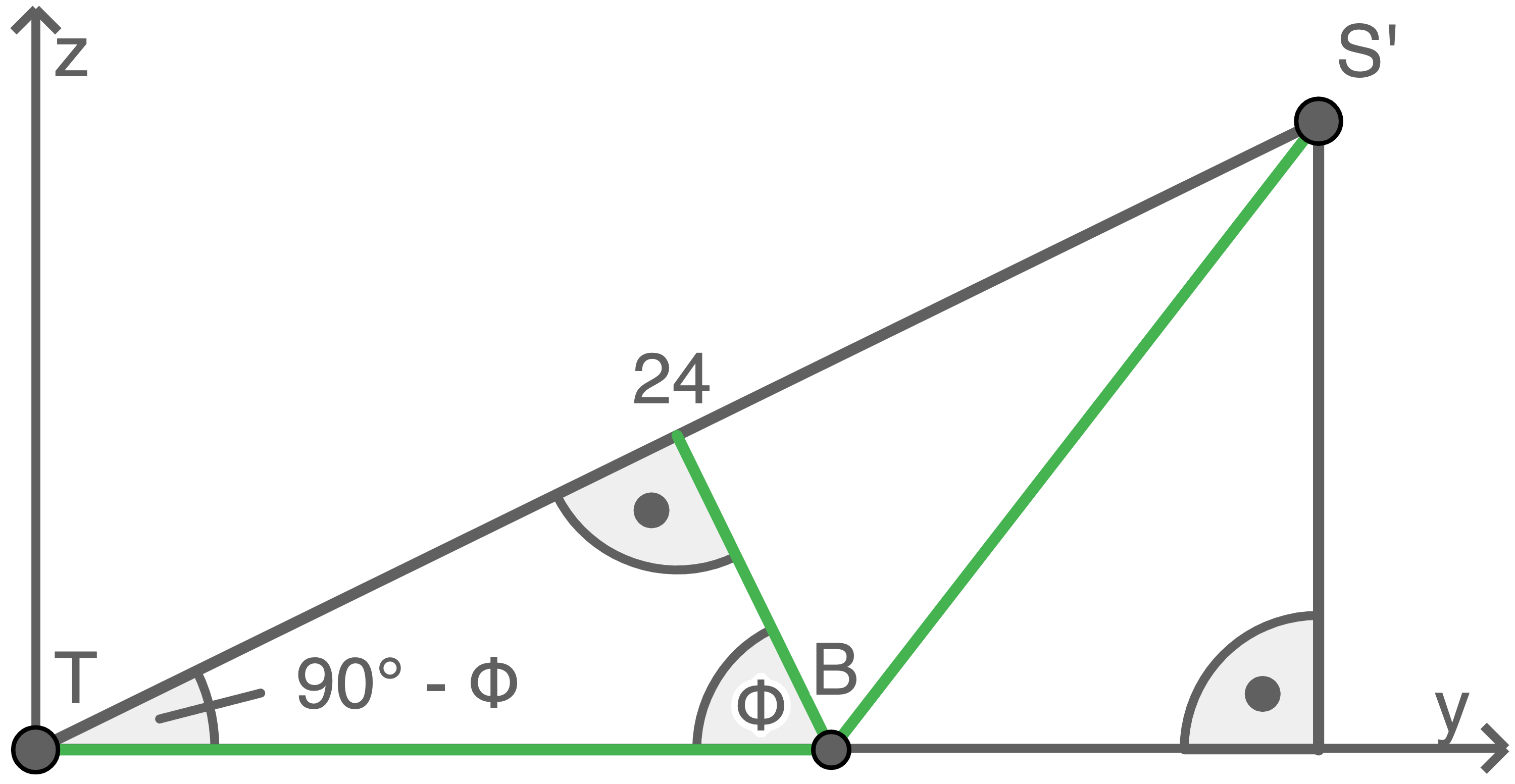Geometrische Darstellung eines Dreiecks mit verschiedenen Winkeln und Längen.

Wird der Doppekegel um den Winkel $\Phi$ im Uhrzeigersinn gekippt, lässt sich der Winkel zwischen der Strecke $\overline{ST}$ und der $y$ -Achse durch $90° - \Phi$ beschreiben. Der Winkel $\Phi$ entspricht dem Winkel zwischen der Ebene $E$ und der $y$ -Achse. Wenn $\overrightarrow{n_E}$ der Normalenvektor der Ebene E und $\overrightarrow{y}$ der Einheitsvektor in Richtung der $y$ -Achse ist, lässt sich $\Phi$ wie folgt bestimmen:

$\begin{array}[t]{rll} \sin(90° - \Phi)&=&\dfrac{\left| \overrightarrow{n_E} \circ \overrightarrow{y} \right|}{\left| \overrightarrow{n_E} \right| \cdot \left| \overrightarrow{y} \right|} &\quad \scriptsize \\[5pt] \sin(90° - \Phi)&=& \dfrac{\left| \pmatrix{0 \\12 \\-5} \circ \pmatrix{0 \\ 1 \\ 0} \right|}{\left| \pmatrix{0 \\12 \\-5} \right| \cdot \left| \pmatrix{0 \\ 1 \\ 0} \right|} &\quad \scriptsize \\[5pt] \sin(90° - \Phi) & = & \dfrac{12}{13 \cdot 1} \qquad \scriptsize \mid \; \sin(\;)^{-1} \\[5pt] 90° - \Phi & \approx & 22,6°& \end{array}$

Damit lässt sich die $y$ -Koordinate des Punktes $\(S$ berechnen.

$\( y_{S$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?