Stochastik

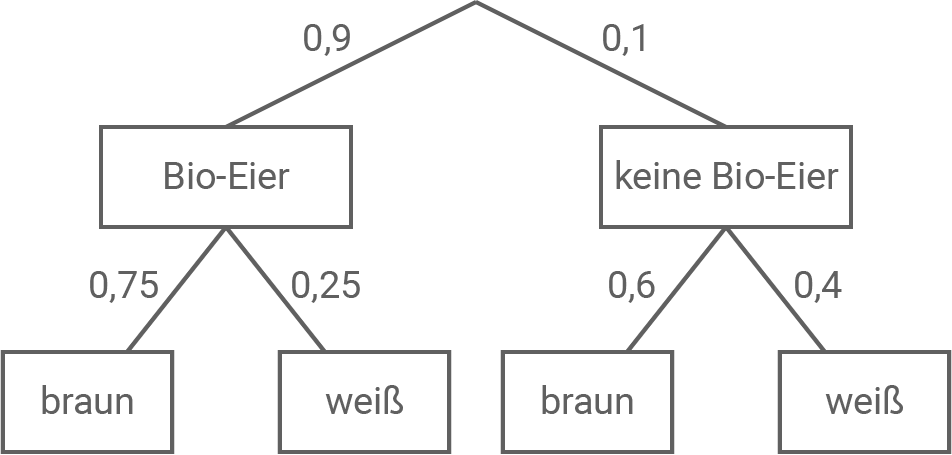
Eine Bäckerei wird regelmäßig von verschiedenen Lieferanten mit Eiern beliefert. Die Lieferungen enthalten zu $90\,\%$ Eier aus ökologischer Tierhaltung (Bio-Eier). Alle anderen gelieferten Eier sind Eier aus Bodenhaltung. Von den Bio-Eiern sind drei Viertel braun, alle anderen weiß. Der Anteil brauner Eier unter den Eiern aus Bodenhaltung beträgt $60\,\%.$

3.1

Stelle diesen Sachverhalt in einem beschrifteten Baumdiagramm dar.

(3 BE)

3.2

In der Bäckerei sind täglich $2000$ Eier vorrätig. Ermittle die Anzahl brauner Eier.

(2 BE)

3.3

Ein zufällig ausgewähltes Ei ist braun. Ermittle die Wahrscheinlichkeit dafür, dass es sich um ein Ei aus Bodenhaltung handelt.

(2 BE)

3.4

Aus einer Kiste mit Bio-Eiern werden $40$ Eier zufällig ausgewählt. Die Zufallsgröße $X$ beschreibt die Anzahl brauner Eier unter den Bio-Eiern und wird im Folgenden als binomialverteilt angenommen.

3.4.1

Begründe ohne Berechnung von Wahrscheinlichkeiten, dass gilt:

$P(28\leq X\leq 32)\gt P(32\leq X\leq 36)$

(3 BE)

3.4.2

Ermittle die Wahrscheinlichkeit dafür, dass sich unter den ausgewählten Eiern mindestens $35$ braune Eier befinden.

(2 BE)

3.4.3

Die Wahrscheinlichkeit eines Ereignisses kann im Sachzusammenhang mit folgendem Term berechnet werden:

Term anzeigen

Ermittle den Wert des Terms und beschreibe das zugehörige Ereignis.

(4 BE)

3.4.4

Nun werden $n$ Bio-Eier zufällig ausgewählt. Die Wahrscheinlichkeit, dass genau zwei dieser Eier weiß sind, ist viermal so groß wie die Wahrscheinlichkeit, dass alle Eier braun sind. Berechne den Wert für $n.$

(5 BE)

3.4.5

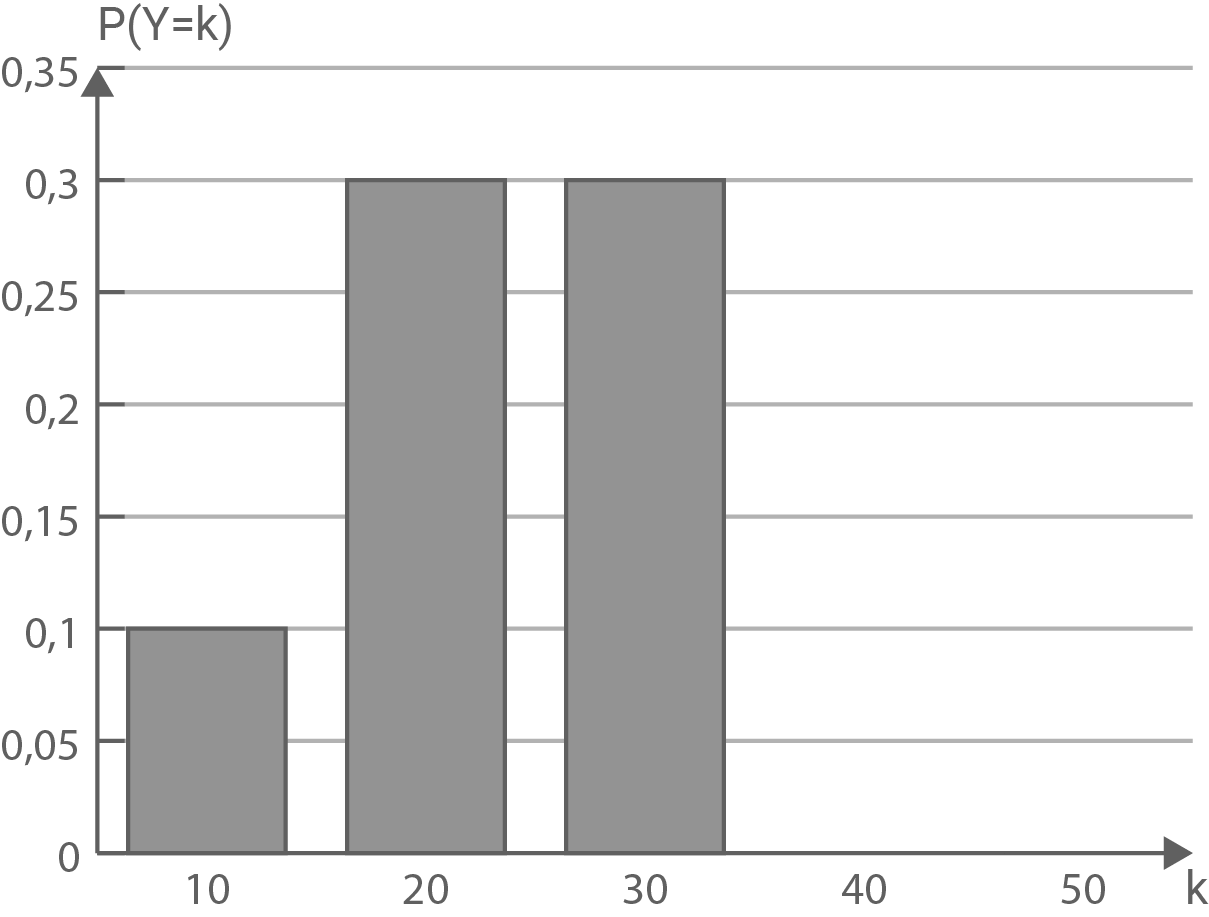
Die Abbildung zeigt den Ausschnitt der Wahrscheinlichkeitsverteilung einer Zufallsgröße $Y.$ Die Erwartungswerte der Zufallsgrößen $X$ und $Y$ sind gleich.

Ermittle die Wahrscheinlichkeiten $P(Y=40)$ und $P(Y=50)$ für diesen Fall.

Mecklenburg-Vorpommern Abi 2022 Wahrscheinlichkeitsverteilung y=40

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?