Analysis
Analysis - Wahlaufgabe
5.
Die Abbildung zeigt den Graphen 
einer in 
definierten Funktion 
sowie den Graphen der ersten Ableitungsfunktion von .
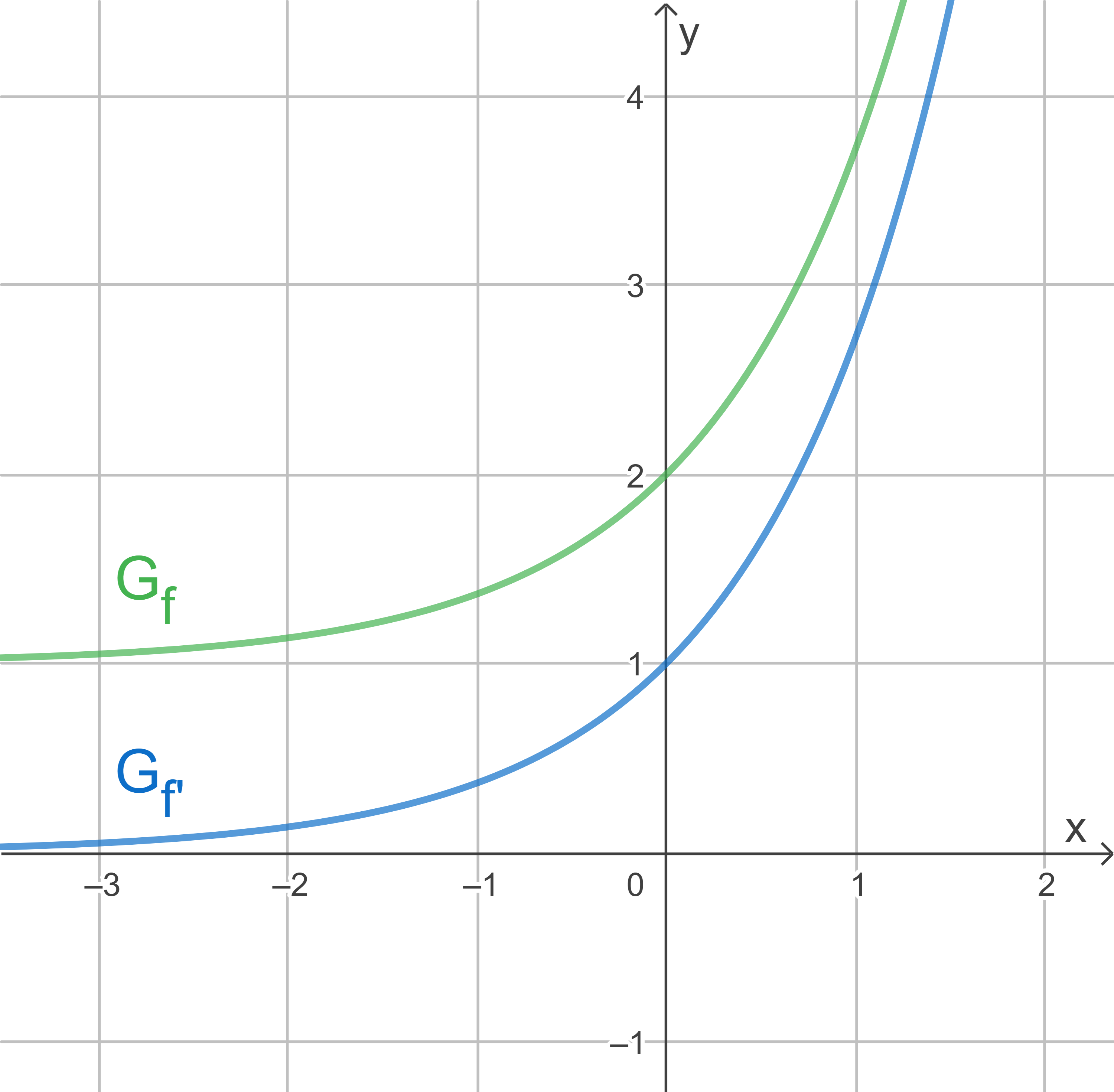
5.1
Gib die Steigung der Tangente an im Punkt 
an.
(1 BE)
5.2
Betrachtet wird die Schar der Funktionen 
mit 
. Der Graph geht aus durch Streckung mit dem Faktor 
in 
-Richtung hervor. Die Tangente an den Graphen von im Punkt 
schneidet die 
-Achse.
Bestimme rechnerisch die-Koordinate des Schnittpunkts.
Bestimme rechnerisch die
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
5.1
Die Steigung der Tangente an im Punkt 
wird durch 
beschrieben. Dieser Wert lässt sich in der gegebenen Abbildung ablesen und beträgt 
5.2
1. Schritt: Tangente im Punkt 
bestimmen
Da für die Funktion die Funtkion um den Faktor in -Achsenrichtung gestreckt wird, gilt 
und 
Damit gilt für die Tangente:
2. Schritt: -Koordinate des Schnittpunkts berechnen
![\(\begin{array}[t]{rlll}
cx+2c&=& 0 & \quad \scriptsize \mid -2c\\[5pt]
cx&=& -2c & \quad \scriptsize \mid :c\\[5pt]
x&=& -2 & \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/03b5d8e0ee2eb982e504d409217a2f37b5e1f01b80762169f208deb348a3ca18?color=5a5a5a)
Damit beträgt die -Koordinate des Schnittpunktes der Tangente mit der -Achse 
Da für die Funktion