Wahlaufgaben
5 Analysis
Gegeben ist für jede positive reelle Zahl  die in
die in  definierte Funktion
definierte Funktion  mit
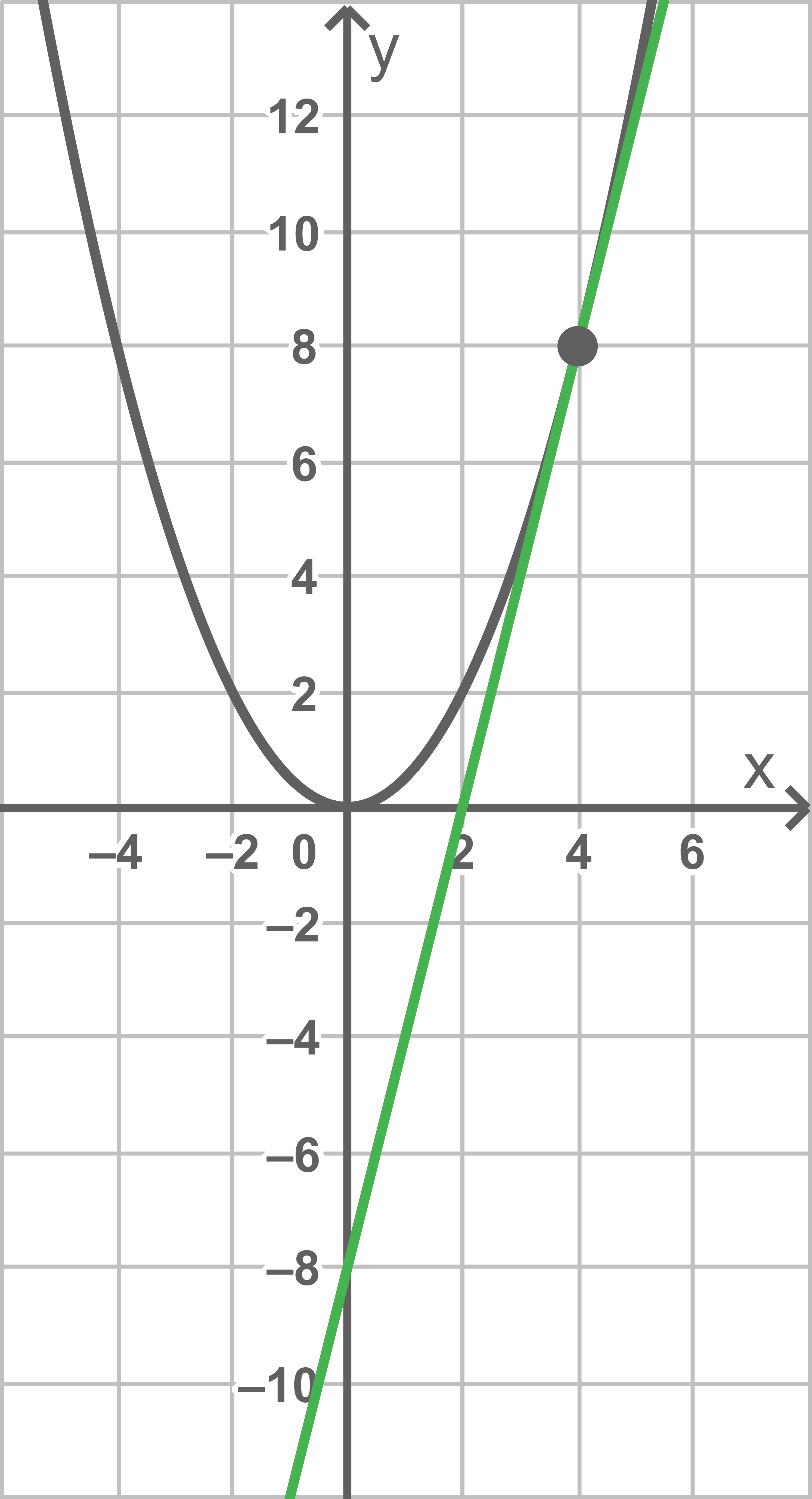
mit  . Die Abbildung zeigt den Graphen von
. Die Abbildung zeigt den Graphen von  sowie die Tangente
sowie die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt 

5.1
Gib anhand der Abbildung eine Gleichung der Tangente  an.
an.
(1 BE)
5.2.
Weise nach, dass für jeden Wert  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  die
die  -Achse im Punkt
-Achse im Punkt  schneidet.
schneidet.
(4 BE)
6 Analysis
Gegeben ist die Funktionenschar
6.1
Zeige für  Die zweite Extremstelle von
Die zweite Extremstelle von  ist
ist 
(2 BE)
6.2
Für jeden Wert von  ist der Graph einer Funktion
ist der Graph einer Funktion  bezüglich des Koordinatenursprungs punktsymmetrisch zum Graphen der Funktion
bezüglich des Koordinatenursprungs punktsymmetrisch zum Graphen der Funktion  .
Weise nach, dass
.
Weise nach, dass  keine Funktion aus der Schar
keine Funktion aus der Schar  ist.
ist.
(3 BE)
7 Analytische Geometrie
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung).
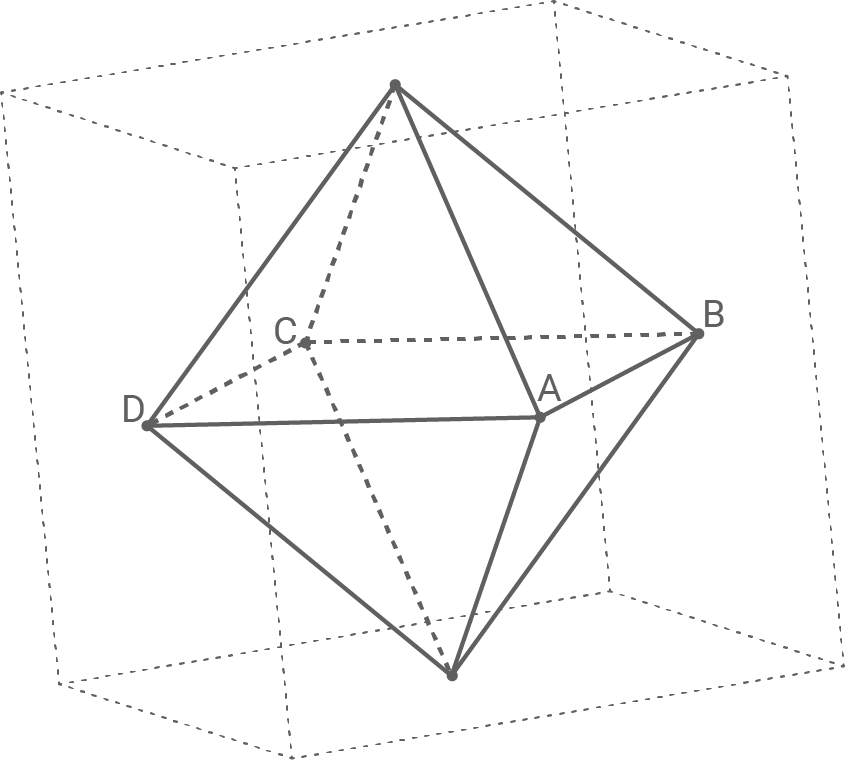 Die Eckpunkte
Die Eckpunkte 

 und
und  des Oktaeders liegen in der Ebene
des Oktaeders liegen in der Ebene  mit der Gleichung
mit der Gleichung 

7.1
Weise nach, dass die Kantenlänge des Würfels 12 beträgt.
(2 BE)
7.2
Bestimme die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in  liegen.
liegen.
(3 BE)
8 Analytische Geometrie
Gegeben sind die Ebenen
8.1
(1 BE)
8.2
Es gibt Punkte in der  -Ebene, die von
-Ebene, die von  den Abstand 10 und von
den Abstand 10 und von  den Abstand 20 haben.
Untersuche, wie viele solcher Punkte existieren.
den Abstand 20 haben.
Untersuche, wie viele solcher Punkte existieren.
(4 BE)
9 Stochastik
Betrachtet wird ein Tetraeder, bei dem die Seiten mit den Zahlen 1 bis 4 durchnummeriert sind. Beim Werfen des Tetraeders werden alle Zahlen mit gleicher Wahrscheinlichkeit erzielt. Das Tetraeder wird viermal geworfen. Die Zufallsgröße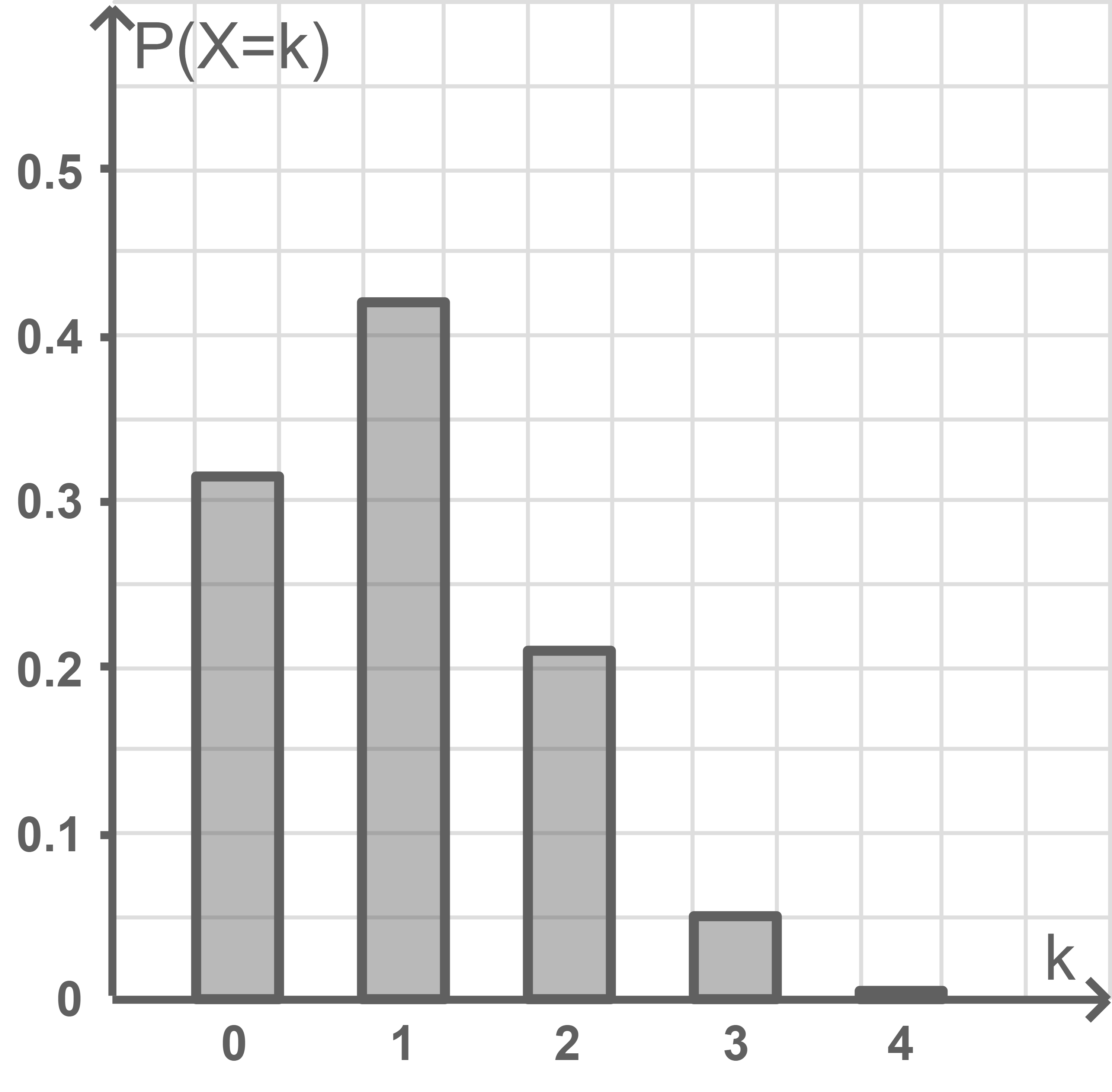
Abb. 1
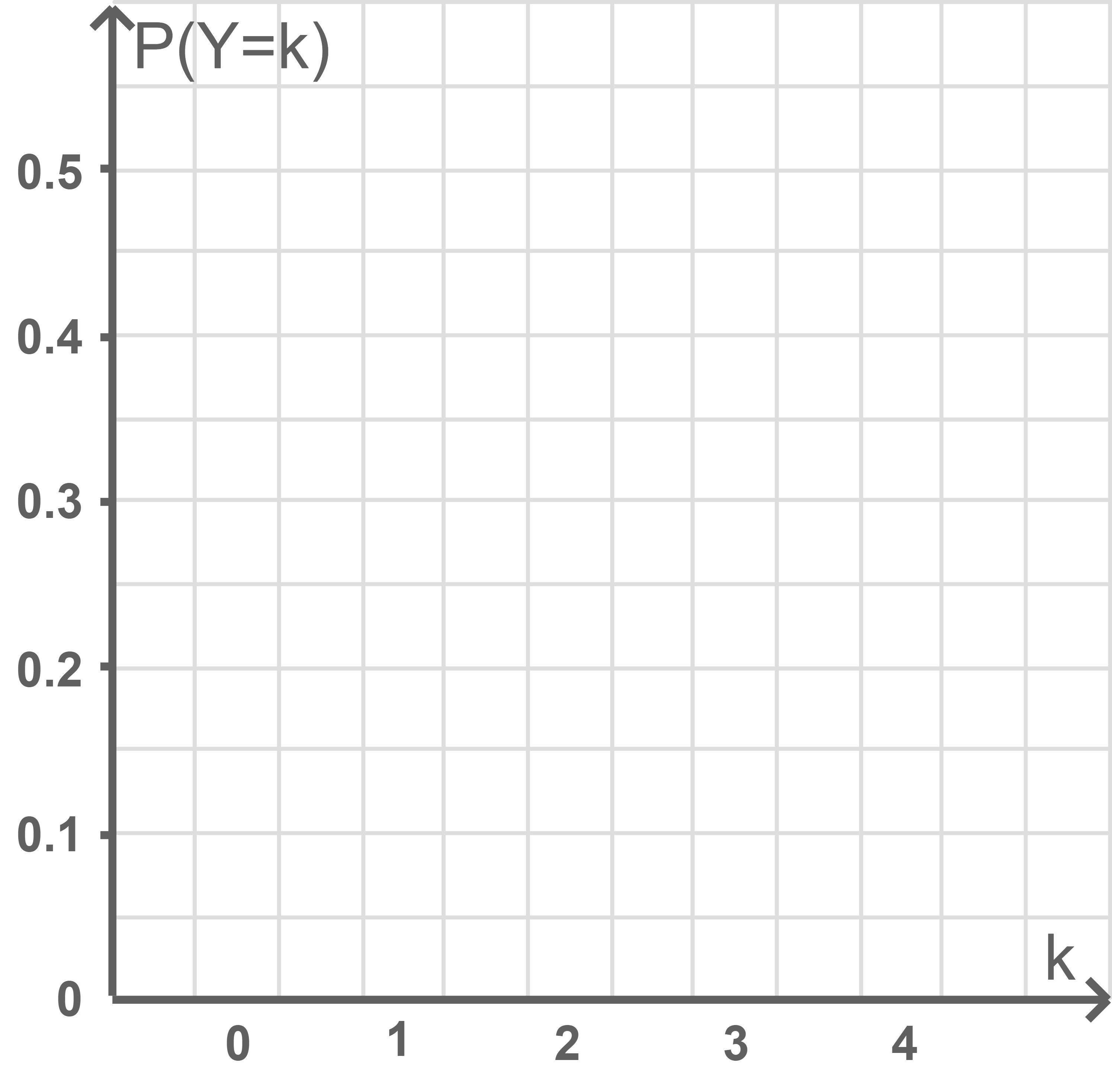
Abb. 2
9.1
Die Zufallsgröße  gibt die Anzahl der Würfe an, bei denen die Zahl 1 nicht erzielt wird. Stelle die Wahrscheinlichkeitsverteilung von
gibt die Anzahl der Würfe an, bei denen die Zahl 1 nicht erzielt wird. Stelle die Wahrscheinlichkeitsverteilung von  in Abbildung 2 dar.
in Abbildung 2 dar.
(2 BE)
9.2
Bei einem anderen Zufallsexperiment werden ein roter und ein grüner Würfel, bei denen die Seiten jeweils mit den Zahlen 1 bis 6 durchnummeriert sind, viermal gleichzeitig geworfen.
Gib zu diesem Zufallsexperiment eine Zufallsgröße  an, die die gleiche Wahrscheinlichkeitsverteilung hat wie
an, die die gleiche Wahrscheinlichkeitsverteilung hat wie  und begründe deine Angabe.
und begründe deine Angabe.
(3 BE)
10 Stochastik

Die drei nicht sichtbaren Seiten des abgebildeten Würfels sollen jeweils mit einer der Zahlen 3, 4, 5 oder 6 beschriftet werden. Dabei können Zahlen auch mehrfach verwendet werden.
Nach der Beschriftung soll der Würfel folgende Eigenschaften haben:
Untersuche, ob es möglich ist, die nicht sichtbaren Seiten des Würfels so zu beschriften, dass er alle drei Eigenschaften besitzt.
- Beim einmaligen Werfen ist der Erwartungswert für die erzielte Zahl gleich 4.
- Auf den sechs Seiten des Würfels kommen genau drei verschiedene Zahlen vor.
- Die Wahrscheinlichkeit dafür, dass beim zweimaligen Werfen des Würfels zweimal die gleiche Zahl erzielt wird, beträgt
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?5 Analysis
5.1
Aus der Abbildung kann die Steigung  sowie der
sowie der  -Achsenabschnitt bei
-Achsenabschnitt bei  der Tangente abgelesen werden.
Eine Gleichung der Tangente ist somit
der Tangente abgelesen werden.
Eine Gleichung der Tangente ist somit 
5.2.
6 Analysis
6.1
Ableitung bestimmen:
![\(\begin{array}[t]{rll}
f_1(x)&=& x^2 \cdot \mathrm e^x& \\[5pt]
f_1](https://mathjax.schullv.de/24489e7f19f202591d40e3ea4b9382661b4655f6144119e8c79270aefae3836b?color=5a5a5a) Notwendige Bedingung für Extremstellen anwenden:
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
f_1](https://mathjax.schullv.de/db88e62f4c8965b838cc50f0754e57fdb68ef53758fdc8a9d67a8140576265fc?color=5a5a5a) Mögliche Extremstellen ergeben sich mit dem Satz vom Nullprodukt also zu
Mögliche Extremstellen ergeben sich mit dem Satz vom Nullprodukt also zu  und
und  Da der Graph von
Da der Graph von  laut Aufgabenstellung genau zwei Extremstellen besitzt, ist das Überprüfen der hinreichenden Bedingung nicht notwendig.
Neben dem Koordinatenursprung ist die zweite Extremstelle somit gegeben durch
laut Aufgabenstellung genau zwei Extremstellen besitzt, ist das Überprüfen der hinreichenden Bedingung nicht notwendig.
Neben dem Koordinatenursprung ist die zweite Extremstelle somit gegeben durch 
6.2
Im Fall einer Punktsymmetrie zum Koordinatenursprung muss gelten:
![\(\begin{array}[t]{rll}
g_a(x)&=& -f_a(-x)&\\[5pt]
&=& -\left((-x)^2 \cdot e^{a \cdot(-x)}\right)&\\[5pt]
&=& -x^2 \cdot e^{-a \cdot x}&\\[5pt]
&\lt & 0
\end{array}\)](https://mathjax.schullv.de/9334e75203e6c7956dc0937397c226689921df91d38b6b8cd3e6226cd269a72b?color=5a5a5a) Wegen
Wegen  und
und  gilt jedoch
gilt jedoch  Da beide Faktoren des Funktionsterms für alle Werte von
Da beide Faktoren des Funktionsterms für alle Werte von  positiv sind, besitzen alle Graphen der Schar
positiv sind, besitzen alle Graphen der Schar  einen positiven Wertebereich, während die Funktion
einen positiven Wertebereich, während die Funktion  nur negative Funktionswerte besitzt.
Die Funktion
nur negative Funktionswerte besitzt.
Die Funktion  kann daher keine Funktion der Schar
kann daher keine Funktion der Schar  sein.
sein.
7 Analytische Geometrie
7.1
7.2
Der Ortsvektor des Mittelpunkts  der Strecke
der Strecke  ergibt sich wie folgt:
ergibt sich wie folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt]
&=&\pmatrix{1\\2\\1}+\dfrac{1}{2}\cdot\pmatrix{-4\\-8\\8} \\[5pt]
&=&\pmatrix{-1\\-2\\5}
\end{array}\)](https://mathjax.schullv.de/f13901135af0ed1192f659481eb360c4523f0a812f6d7c78db8b4d46d714bd89?color=5a5a5a) Aus der Ebenengleichung von
Aus der Ebenengleichung von  lässt sich zudem der folgende Normalenvektor ablesen:
lässt sich zudem der folgende Normalenvektor ablesen:
 Es gilt
Es gilt 
 Da die Kantenlänge des Würfels 12 beträgt, ist der Abstand des gesuchten Eckpunktes des Oktaeders zu
Da die Kantenlänge des Würfels 12 beträgt, ist der Abstand des gesuchten Eckpunktes des Oktaeders zu  durch 6 Längeneinheiten gegeben. Ein möglicher Ortsvektor ergibt sich somit zu:
durch 6 Längeneinheiten gegeben. Ein möglicher Ortsvektor ergibt sich somit zu:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}+2\cdot\overrightarrow{n}&=&\pmatrix{-1\\-2\\5}+2\cdot\pmatrix{2\\1\\2} \\[5pt]
&=&\pmatrix{3\\0\\9}
\end{array}\)](https://mathjax.schullv.de/04ec95577f1efba0c8c2541cc42cf6b5b46ccc1848f3bfc031c3117bb2f34c68?color=5a5a5a) Mögliche Koordinaten für den gesuchten Punkt sind somit gegeben durch
Mögliche Koordinaten für den gesuchten Punkt sind somit gegeben durch 
8 Analytische Geometrie
8.1
Da die Ebenengleichungen von  und
und  keine
keine  -Koordinate enthalten und somit unabhängig von dieser verlaufen, liegen die beiden Ebenen parallel zur
-Koordinate enthalten und somit unabhängig von dieser verlaufen, liegen die beiden Ebenen parallel zur  -Achse und stehen somit senkrecht auf der
-Achse und stehen somit senkrecht auf der  -Ebene.
Alternative Begründung:
Aus den Ebenengleichungen lassen sich folgende Normalenvektoren ablesen:
-Ebene.
Alternative Begründung:
Aus den Ebenengleichungen lassen sich folgende Normalenvektoren ablesen:
 und
und  Ein Normalenvektor der
Ein Normalenvektor der  -Ebene ist gegeben durch
-Ebene ist gegeben durch  Zwei Ebenen stehen genau dann senkrecht aufeinander, wenn das Skalarprodukt ihrer Normalenvektoren null ergibt:
Zwei Ebenen stehen genau dann senkrecht aufeinander, wenn das Skalarprodukt ihrer Normalenvektoren null ergibt:
![\(\begin{array}[t]{rll}
\overrightarrow{n_E} \circ \overrightarrow{n_{xy}} &=& \pmatrix{1\\1\\0}\circ \pmatrix{0\\0\\1} & \\[5pt]
&=& 1\cdot 0+1\cdot 0+0\cdot 1 & \\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/afbc2e56e946c31f5ab4f9f4a3e70442f118ec6d58efa0e916f172a2868d73f4?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{n_F} \circ \overrightarrow{n_{xy}} &=& \pmatrix{1\\-1\\0}\circ \pmatrix{0\\0\\1} & \\[5pt]
&=& 1\cdot 0-1\cdot 0+0\cdot 1 & \\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/b9d3645975ce86bb3f4fb54b1e3b124fc7df285d3749882271cc91c3d7bb79e6?color=5a5a5a)
8.2
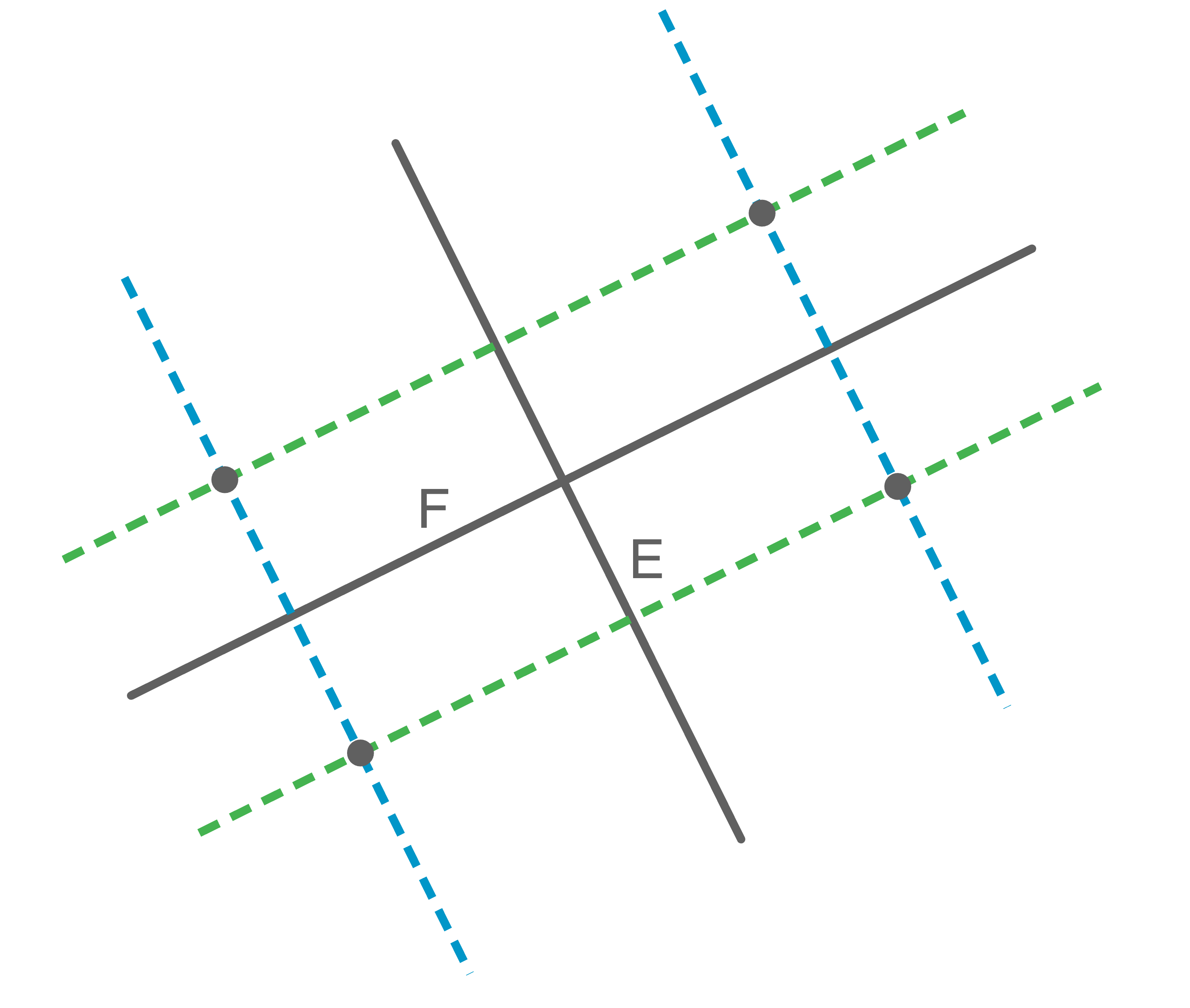
Hilfsskizze
Dargestellt sind mit durchgehenden Linien die Schnittgeraden von  und
und  mit der
mit der  -Ebene sowie jeweils dazu parallel verlaufende Geraden mit den Abständen 10 (grün gestrichelt) bzw. 20 (blau gestrichelt).
Die zu den Schnittgeraden parallel verlaufenden Geraden schneiden sich viermal. Somit gibt es 4 solcher Punkte.
-Ebene sowie jeweils dazu parallel verlaufende Geraden mit den Abständen 10 (grün gestrichelt) bzw. 20 (blau gestrichelt).
Die zu den Schnittgeraden parallel verlaufenden Geraden schneiden sich viermal. Somit gibt es 4 solcher Punkte.
9 Stochastik
9.1
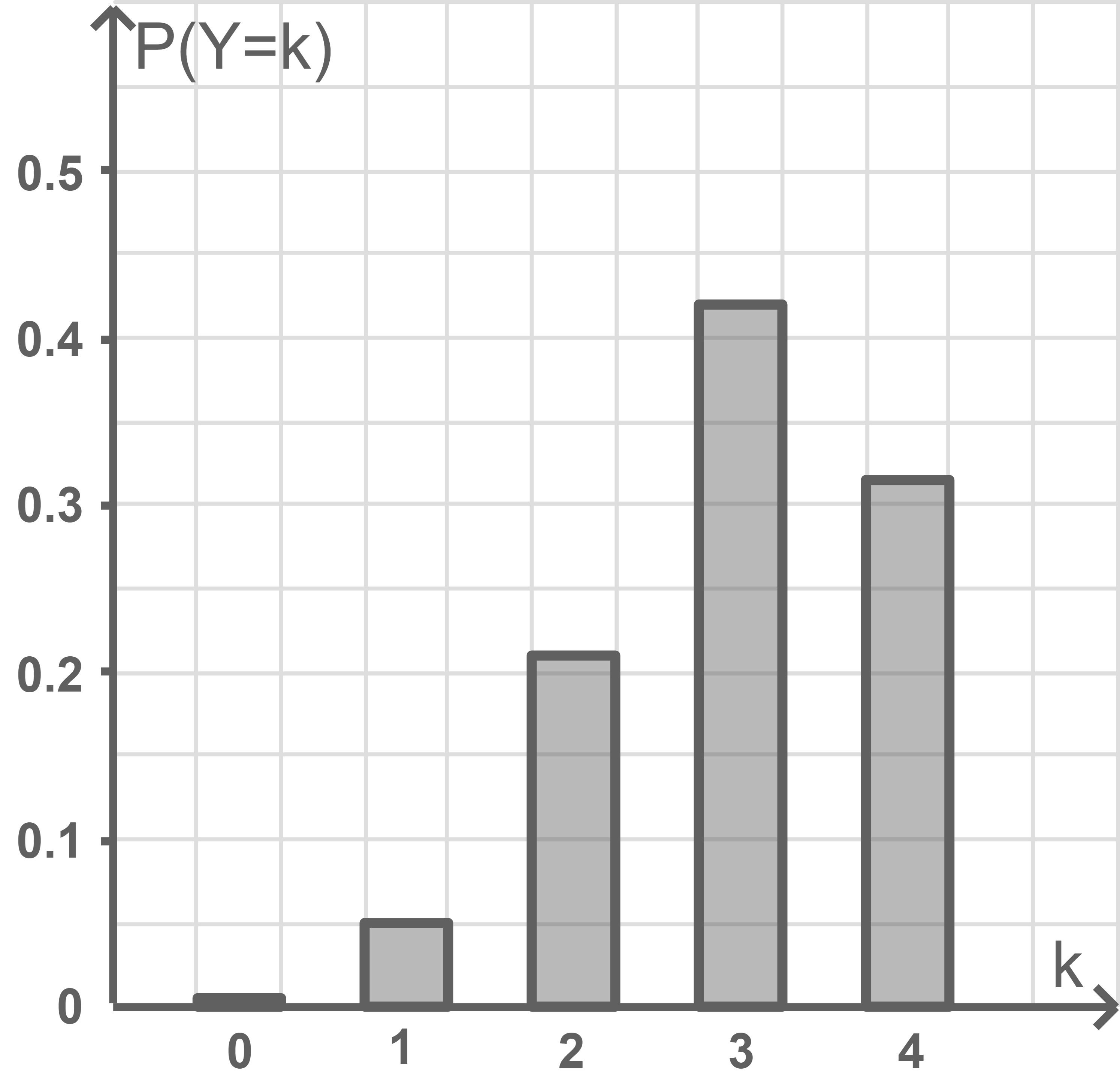
9.2
Zufallsgröße angeben
 Anzahl der Würfe, bei denen keine der beiden gewürfelten Zahlen größer als 3 ist.
Angabe begründen
Beim einmaligen Werfen der beiden Würfel gibt es insgesamt
Anzahl der Würfe, bei denen keine der beiden gewürfelten Zahlen größer als 3 ist.
Angabe begründen
Beim einmaligen Werfen der beiden Würfel gibt es insgesamt  mögliche Ergebnisse, die alle gleich wahrscheinlich sind. Die Ergebnisse, bei denen keine der beiden Zahlen größer als 3 ist, ergeben sich wie folgt:
mögliche Ergebnisse, die alle gleich wahrscheinlich sind. Die Ergebnisse, bei denen keine der beiden Zahlen größer als 3 ist, ergeben sich wie folgt:

 Die Wahscheinlichkeit, beim einmaligen Würfeln keine Zahl zu erzielen, die größer als 3 ist, ergibt sich somit zu
Die Wahscheinlichkeit, beim einmaligen Würfeln keine Zahl zu erzielen, die größer als 3 ist, ergibt sich somit zu  Die Zufallsgrößen
Die Zufallsgrößen  und
und  sind somit beide binomialverteilt mit
sind somit beide binomialverteilt mit  und
und  das heißt sie besitzen die gleiche Wahrscheinlichkeitsverteilung.
das heißt sie besitzen die gleiche Wahrscheinlichkeitsverteilung.