Analysis
1.1
Ein Teil der Atomkerne eines Präparates ist radioaktiv. Für die Beschreibung der Masse dieser radioaktiven Atomkerne im Präparat kann die Funktion  mit
mit  und
und  verwendet werden. Dabei gibt
verwendet werden. Dabei gibt  die Masse der vorhandenen radioaktiven Atomkerne in Milligramm an. Die seit Beobachtungsbeginn vergangene Zeit wird mit
die Masse der vorhandenen radioaktiven Atomkerne in Milligramm an. Die seit Beobachtungsbeginn vergangene Zeit wird mit  in Sekunden angegeben. Zu Beginn der Beobachtung beträgt diese Masse
in Sekunden angegeben. Zu Beginn der Beobachtung beträgt diese Masse  ,
,  später noch
später noch 
1.1.1
Ermittle für den angegebenen Sachverhalt die Werte von  und
und  Runde dabei den Wert von
Runde dabei den Wert von  auf zwei Nachkommastellen.
zur Kontrolle:
auf zwei Nachkommastellen.
zur Kontrolle: 
 Berechne den Zeitpunkt, zu dem sich die Masse der vorhandenen radioaktiven Kerne halbiert hat.
Berechne den Zeitpunkt, zu dem sich die Masse der vorhandenen radioaktiven Kerne halbiert hat.
(4 BE)
1.1.2
Die Masse der vorhandenen radioaktiven Atomkerne in Milligramm kann im Zeitraum  näherungsweise auch durch eine lineare Funktion
näherungsweise auch durch eine lineare Funktion  beschrieben werden.
Dabei gilt:
beschrieben werden.
Dabei gilt:  und
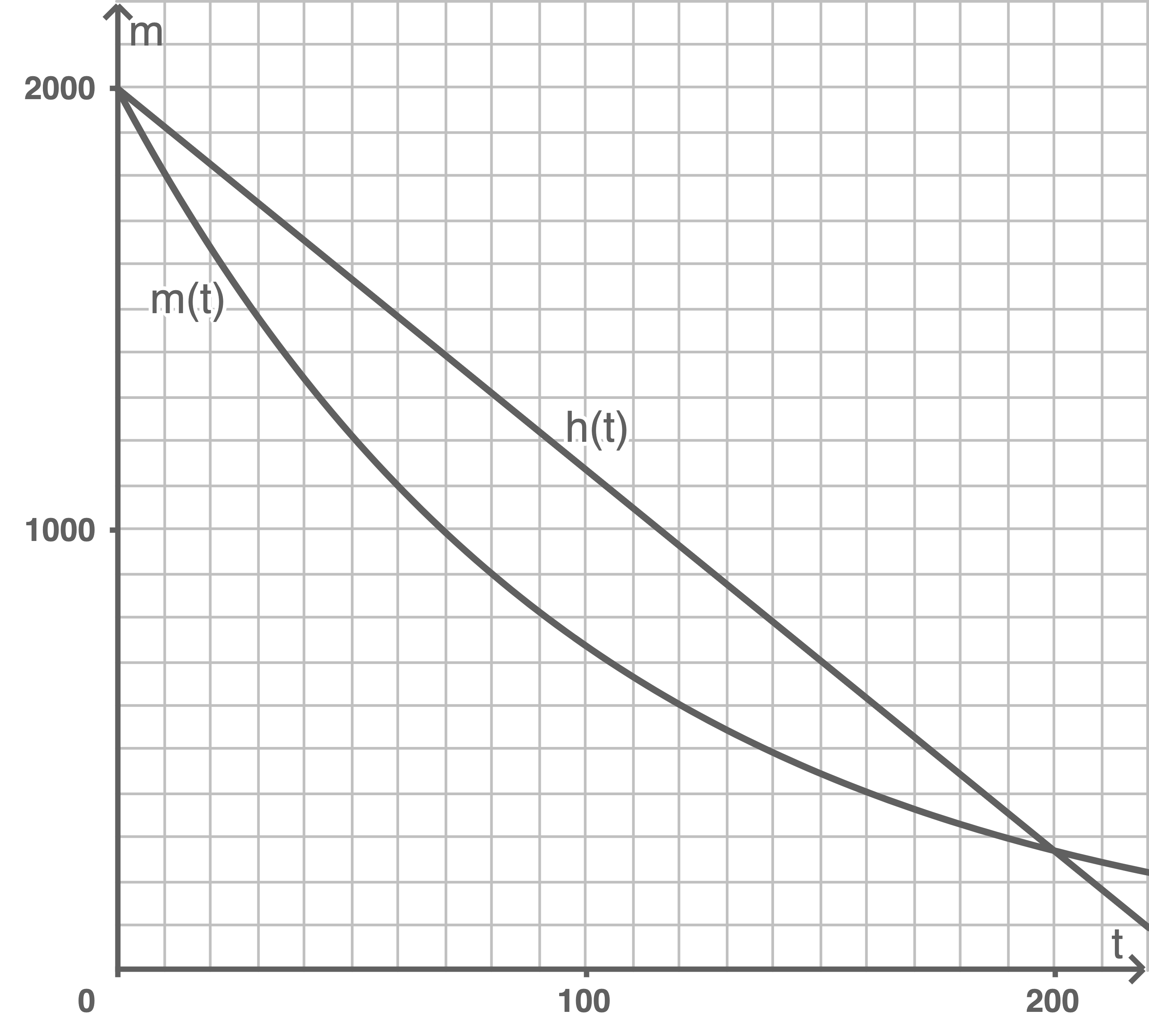
und  Zeichne die Graphen der Funktionen
Zeichne die Graphen der Funktionen  und
und  in ein gemeinsames Koordinatensystem.
Ermittle eine Gleichung der Funktion
in ein gemeinsames Koordinatensystem.
Ermittle eine Gleichung der Funktion  zur Kontrolle: Anstieg von
zur Kontrolle: Anstieg von  etwa
etwa 
(4 BE)
1.1.3
Berechne den Zeitpunkt  für den sich die durch die Funktionen
für den sich die durch die Funktionen  und
und  modellierten Massen am stärksten unterscheiden.
Weise das Maximum nach. Gib das Maximum an.
modellierten Massen am stärksten unterscheiden.
Weise das Maximum nach. Gib das Maximum an.
(6 BE)
1.2
Betrachtet wird die Funktion  mit
mit  mit
mit  .
.  ist diejenige Stammfunktion von
ist diejenige Stammfunktion von  mit
mit  Ermittle eine Gleichung von
Ermittle eine Gleichung von  Begründe, dass für den Wertebereich von
Begründe, dass für den Wertebereich von  gilt:
gilt:  Zeige, dass gilt:
Zeige, dass gilt: 
(5 BE)
1.3
Gegeben sind die Funktionen  mit
mit  und
und  mit
mit  und
und  An derselben Stelle wird jeweils eine Tangente an den Graphen von
An derselben Stelle wird jeweils eine Tangente an den Graphen von  und an den Graphen von
und an den Graphen von  gelegt.
Begründe, dass der Schnittwinkel der beiden Tangenten unabhängig von den Parametern
gelegt.
Begründe, dass der Schnittwinkel der beiden Tangenten unabhängig von den Parametern  und
und  ist.
ist.
(5 BE)
1.4
Gegeben ist die Funktion  durch
durch  mit
mit  Der Graph von
Der Graph von  ist
ist 
1.4.1
Begründe, dass folgende Aussagen wahr sind:
I.  ist an der Stelle
ist an der Stelle  rechtsgekrümmt
II:
rechtsgekrümmt
II: 
(5 BE)
1.4.2
(5 BE)
1.4.3
Für jeden reellen Wert von  wird im Punkt
wird im Punkt  mit
mit  die Tangente und die Normale an
die Tangente und die Normale an  gelegt.
Ermittle eine Gleichung der Tangente in Abhängigkeit von
gelegt.
Ermittle eine Gleichung der Tangente in Abhängigkeit von  Begründe, dass der Anstieg jeder dieser Normalen negativ ist.
Begründe, dass der Anstieg jeder dieser Normalen negativ ist.
(6 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1.1
Wert von 
 also
also  Wert von
Wert von 
![\(\begin{array}[t]{rll}
m(30)&=&1472 \\[5pt]
2000\cdot \mathrm e^{(-30k)}&=&1472\quad \scriptsize \mid\;:2000\\[5pt]
\mathrm e^{(-30k)}&=&\dfrac{1472}{2000}\quad \scriptsize \mid\;\ln()\\[5pt]
-30k&=&\ln\left(\dfrac{1472}{2000}\right)\quad \scriptsize \mid\;:(-30)\\[5pt]
k&\approx&0,01
\end{array}\)](https://mathjax.schullv.de/0e5d989923215f2a606c1a8fcb565b50c9f1a68fccd65b8a37f133534f13c1bb?color=5a5a5a) Zeitpunkt berechnen
Zeitpunkt berechnen
![\(\begin{array}[t]{rll}
2000\cdot \mathrm e^{\left(-0,01\cdot t\right)}&=&1000\quad \scriptsize \mid\;:2000 \\[5pt]
\mathrm e^{\left(-0,01\cdot t\right)}&=&\dfrac{1}{2}\quad \scriptsize \mid\;\ln()\\[5pt]
-0,01\cdot t&=&\ln\left(\dfrac{1}{2}\right)\quad \scriptsize \mid\;:(-0,01)\\[5pt]
t&\approx&69
\end{array}\)](https://mathjax.schullv.de/46ba9bbb06617d71250f323f1e69914b3d8196b7d28571c8af16c569edfa7d97?color=5a5a5a) Nach 69 Sekunden hat sich die betrachtete Masse halbiert.
Nach 69 Sekunden hat sich die betrachtete Masse halbiert.
1.1.2
1.1.3
1.2
1.3
Ableitungsfunktionen aufstellen:

 Die beiden Ableitungsfunktionen werden nun miteinander multipliziert:
Die beiden Ableitungsfunktionen werden nun miteinander multipliziert:


 Wenn die Steigungen von zwei Tangenten miteinander multipliziert werden und
Wenn die Steigungen von zwei Tangenten miteinander multipliziert werden und  ergeben, dann sind diese senkrecht zueinander. Der Schnittwinkel beträgt deshalb unabhängig von
ergeben, dann sind diese senkrecht zueinander. Der Schnittwinkel beträgt deshalb unabhängig von  und
und  immer
immer 
1.4.1
Aussage I



 ist an der Stelle
ist an der Stelle  also rechtsgekrümmt.
Aussage II
also rechtsgekrümmt.
Aussage II


 Aus dem Hauptsatz der Differential- und Integralrechnung folgt somit Aussage II.
Aus dem Hauptsatz der Differential- und Integralrechnung folgt somit Aussage II.
1.4.2
Zunächst werden die Nullstellen berechnet:
 daraus folgt:
daraus folgt: 
 und
und  Inhalt der ersten Fläche:
Inhalt der ersten Fläche:

![\(=[\sin(x)-x\cdot \cos(x)]_0^\pi=\pi-0=\pi\)](https://mathjax.schullv.de/5de3209a295e81601975017b61378e904945aec2afb7756e51a7c407d6d5e750?color=5a5a5a) Inhalt der zweiten Fläche:
Inhalt der zweiten Fläche:

![\(=[\sin(x)-x\cdot \cos(x)]_\pi^{2\pi}=-2\pi-\pi=-3\pi\)](https://mathjax.schullv.de/02005113f42ba86f3889ee84798d30f584b16f487d3728e7feca28aa72aa9e49?color=5a5a5a) Verhältnis berechnen:
Verhältnis berechnen:
 Das Verhältnis ist also
Das Verhältnis ist also 
1.4.3
Tangentengleichung ermitteln
Die allg. Tangentengleichung lautet:  Steigung ermitteln
Steigung ermitteln

 -Achsen-Abschnitt ermitteln
Die allg. Tangentengleichung umgeformt ergibt:
-Achsen-Abschnitt ermitteln
Die allg. Tangentengleichung umgeformt ergibt:


 Die Tangentengleichung lautet also
Die Tangentengleichung lautet also  Begründen
Für
Begründen
Für  sind
sind 
 und
und  positiv, somit hat jede Tangente mit
positiv, somit hat jede Tangente mit  auch einen positiven Anstieg. Jede Normale hat den negativen Anstieg
auch einen positiven Anstieg. Jede Normale hat den negativen Anstieg 