2 Analysis und Analytische Geometrie

2.1

Gegeben ist die Funktion $f$ mit der Gleichung $f(x)=-\mathrm{e}^x+2$ und $x \in \mathbb{R}.$ Der Graph von $f$ ist in der Abbildung 1 für $x \geq-1$ dargestellt.

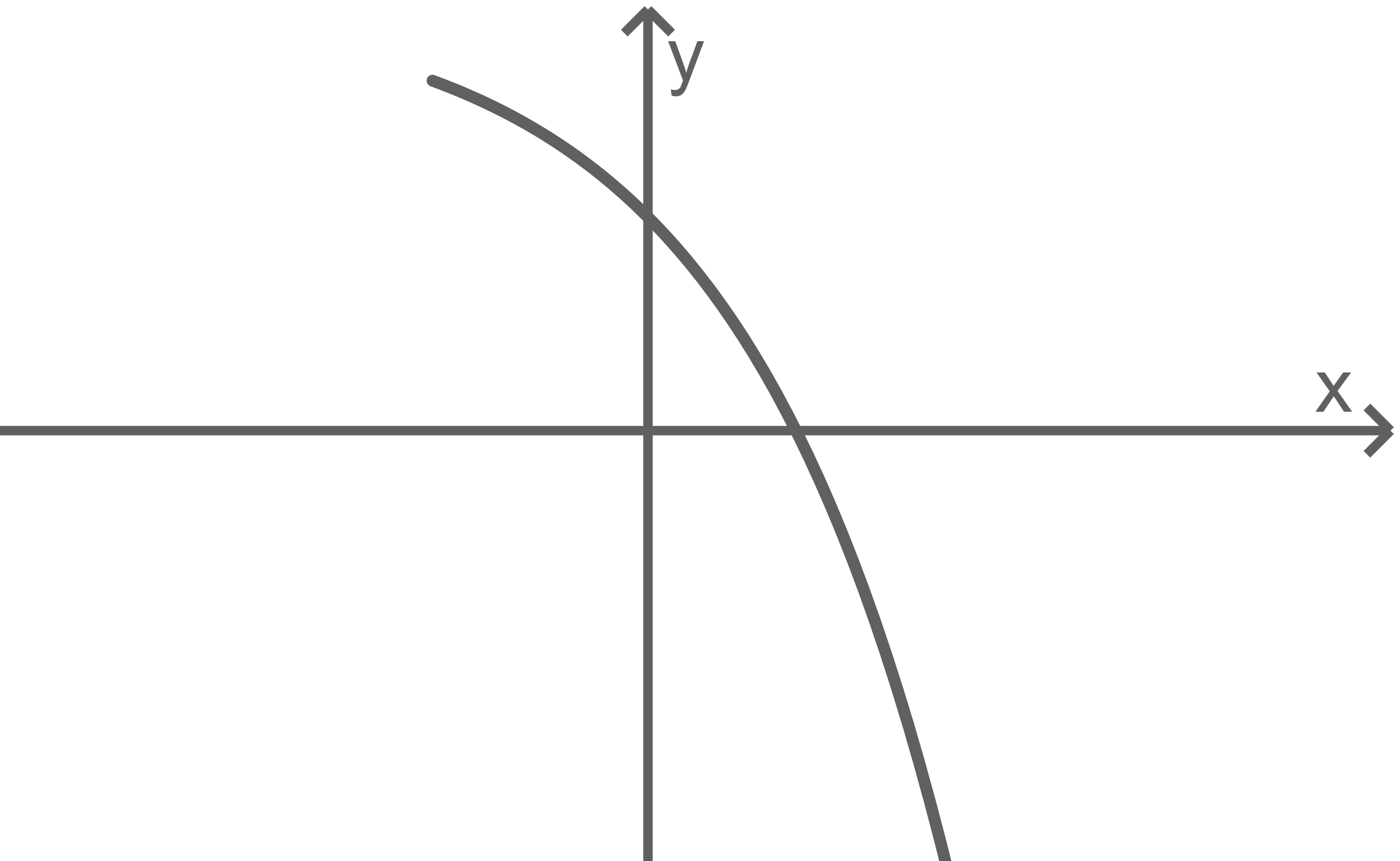
Abb. 1

2.1.1

Weise nach, dass $(0\mid1)$ der Schnittpunkt des Graphen von $f$ mit der $y$ -Achse ist. Berechne die Nullstelle von $f.$

(3 BE)

2.1.2

An den Graphen von $f$ wird in seinem Schnittpunkt mit der $y$ -Achse die Tangente $t$ gelegt. Diese Tangente, die Gerade $x=-2$ und die $x$ -Achse schließen ein Dreieck ein. Berechne den Inhalt dieser Dreiecksfläche.

(5 BE)

2.1.3

Begründe ohne Rechnung, dass gilt: $\displaystyle\int_{-2024}^{-2023}f(x)\;\mathrm dx\approx 2.$

(2 BE)

2.2

Die Punkte $A(5\mid0\mid 0),$ $B(0\mid3\mid 0),$ $C(0\mid0\mid 0)$ und $S(0\mid2\mid 10)$ bilden eine Pyramide $P$ mit der Grundfläche $ABC$ und der Spitze $S$ (siehe Abbildung 2).

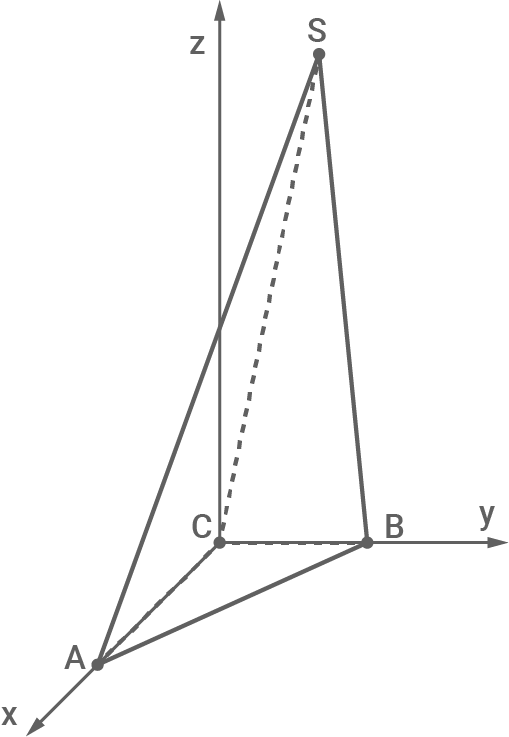
Abb. 2

2.2.1

Begründe, dass $ABC$ ein rechtwinkliges Dreieck ist, und gib dessen Flächeninhalt an.

(3 BE)

2.2.2

Es gibt eine Ebene $E,$ in der die Punkte $A, B$ und $S$ liegen.
Ermittle eine Gleichung von $E$ in Koordinatenform.

Zur Kontrolle: $E: 6x+10y+z=30$

(4 BE)

2.2.3

Gib eine Gleichung der Gerade $g$ an, die durch den Punkt $A$ verläuft und orthogonal auf der Ebene $E$ steht.

(1 BE)

2.2.4

Betrachtet werden die Pyramiden $ABCS_k$ mit der Spitze $S_k(0\mid k\mid 10).$
Gib alle ganzzahligen Werte von $k$ an, sodass die Kante $\overline{AS_k},$ die Kante $\overline{BS_k}$ oder die Kante $\overline{CS_k}$ die Höhe einer der Pyramiden ist.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

2.1.1

Einsetzen von $x=0$ in $f(x)$ liefert:

$\begin{array}[t]{rll} f(0)&=&-\mathrm{e}^0 + 2 \\[5pt] &=&-1 + 2 \\[5pt] &=&1 \end{array}$

Somit ist $(0\mid1)$ der Schnittpunkt des Graphen von $f$ mit der $y$ -Achse.
Die Gleichung $f(x)=0$ liefert für die gesuchte Nullstelle:

$\begin{array}[t]{rll} f(x)&=&0 \\[5pt] -\mathrm{e}^x + 2&=&0 &\quad \scriptsize \mid\;+\mathrm e^x \\[5pt] 2&=&\mathrm e^x \\[5pt] \ln(2)&=&x \end{array}$

Die Nullstelle von $f$ ist damit $x = \ln(2).$

2.1.2

Die betrachtete Tangente $t$ hat die allgemeine Gleichung $t(x)=mx+n.$ Für die Ableitung von $f$ gilt:

$\(f$

Einsetzen von $x=0$ in $\(f$ liefert $m=-\mathrm e^0=-1.$ Da die Tangente an dem Schnittpunkt $(0\mid1)$ mit der $y$ -Achse anliegt, gilt $n=1$ und es folgt $t(x)=-x+1.$

Die Tangente hat damit die Nullstelle $x=1,$ das heißt die Basis des Dreiecks ist $1-(-2)=3\;\text{LE}$ lang. Die zu dieser Basis gehörende Höhe $h$ ist durch den $y$ -Wert der Tangente bei $x=-2$ gegeben, das heißt es folgt:

$\begin{array}[t]{rll} h&=&t(-2) \\[5pt] &=&-(-2) + 1 \\[5pt] &=&3\;\text{LE} \end{array}$

Somit folgt für den Flächeninhalt des Dreiecks $A=\frac{1}{2}\cdot3\cdot3=4,5\;[\text{LE}].$

2.1.3

Für $x\to-\infty$ nähert sich $f(x)$ dem Wert $2$ an, da $-\mathrm{e}^x$ gegen Null geht. Daher kann das Integral von $f(x)$ über ein Intervall der Länge $1$ für große negative Werte als Flächeninhalt eines Rechtecks mit der Breite $1$ und Höhe $2$ beschrieben werden.

2.2

2.2.1

Rechten Winkel begründen

Das Dreieck $ABC$ ist rechtwinklig, da $C(0\mid0\mid0)$ der Ursprung ist und die Seiten $\overline{AC}$ und $\overline{BC}$ entlang der Achsen verlaufen.

Flächeninhalt angeben

Aus den Koordinaten der Punkte $A, B$ und $C$ lässt sich direkt ablesen, dass die Längen der Seiten $\overline{AC}$ bzw. $\overline{BC}$ durch $5\;\text{LE}$ bzw. $3\;\text{LE}$ gegeben sind. Somit folgt für den gesuchten Flächeninhalt $A=\frac{1}{2} \cdot 5 \cdot 3 = 7,5\;[\text{FE}].$

2.2.2

Die Parameterform der Ebene lautet: $\vec{r}=\overrightarrow{O A}+r \cdot \overrightarrow{A B}+s \cdot \overrightarrow{A S}$

Die komponentenweise Darstellung lautet dann:

$\pmatrix{x\\y\\z}=\left(\begin{array}{l} 5 \\ 0 \\ 0 \end{array}\right)+r\left(\begin{array}{c} -5 \\ 3 \\ 0 \end{array}\right)+s\left(\begin{array}{c} -5 \\ 2 \\ 10 \end{array}\right)$

Daraus ergeben sich die folgenden Gleichungen:

$x=5-5 r-5 s$

$y=3 r+2 s$

$z=10 s$

Aus der Gleichung für $z$ folgt:

$\begin{array}[t]{rll} z&=& 10s \quad \scriptsize \mid\; :10 \\[5pt] \dfrac{z}{10}&=& s \end{array}$

Einsetzen von $s$ in die Gleichung für $y$ liefert:

$\begin{array}[t]{rll} y&=& 3r+2\cdot \dfrac{z}{10} &\quad \scriptsize \mid\; -\dfrac{z}{5} \\[5pt] y-\dfrac{z}{5}&=& 3r &\quad \scriptsize \mid\; :3 \\[5pt] \dfrac{y}{3}-\dfrac{z}{15}&=& r \end{array}$

Einsetzen von $r$ und $s$ in die Gleichung für $x$ liefert schließlich:

$\begin{array}[t]{rll} x&=& 5-5\left(\dfrac{y}{3}-\dfrac{z}{15}\right)-5\left(\dfrac{z}{10}\right) \\[5pt] x&=& 5-\dfrac{5y}{3}+\dfrac{z}{3}-\dfrac{z}{2} \\[5pt] x&=& 5-\dfrac{5y}{3}-\dfrac{z}{6} \quad \scriptsize \mid\; \cdot 6\\[5pt] 6x&=& 30-10y-z \quad \scriptsize \mid\; +10y+z\\[5pt] 6x+10y+z&=& 30 \end{array}$

2.2.3

Ein möglicher Richtungsvektor aller Geraden, die orthogonal zur Ebene $E$ verlaufen, ist der Normalevektor von $E.$ Die Gerade $g,$ die durch den Punkt $A$ und orthogonal zur Ebene $E$ verläuft hat somit die mögliche folgende Gleichung:

$g: \overrightarrow{x} = \pmatrix{5\\0\\0} + r\cdot\pmatrix{6\\10\\1}$

2.2.4

Damit eine der Kanten $\overline{AS_k}, \overline{BS_k}$ oder $\overline{CS_k}$ die Höhe einer der Pyramiden ist, müssen sich die Punkte $A, B$ oder $C$ jeweils nur in der $z$ -Koordinate von $S_k$ unterscheiden. Somit sind $k=0$ und $k=3$ die einzigen möglichen Werte.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?