Wahlteil B2
B2 Analytische Geometrie und Stochastik
In Hamburg steht am Ufer der Elbe ein Bürogebäude (siehe Abbildung). Die markante Stahl-Glas-Konstruktion ruht auf Betonpfeilern. Zwei Seitenwände des Gebäudes stehen lotrecht (senkrecht zur Erdoberfläche), die anderen beiden nicht.
Abb. 1: Ansicht des Hamburger Bürogebäudes von Norden
der Kante
2.1
Bestimme die Koordinaten der Eckpunkte der Fläche  und stelle den Körper
und stelle den Körper  grafisch dar.
(zur Kontrolle:
grafisch dar.
(zur Kontrolle: 
(5 BE)
2.2
Berechne das Volumen des Gebäudes.
(2 BE)
2.3
Bestimme eine Koordinatengleichung der Ebene, in der die Fläche  liegt.
Berechne den Neigungswinkel der nicht lotrechten Seitenwände des Bürogebäudes.
(zur Kontrolle:
liegt.
Berechne den Neigungswinkel der nicht lotrechten Seitenwände des Bürogebäudes.
(zur Kontrolle: 
(5 BE)
2.4
Auf dem Dach eines Hauses am nördlichen Elbufer ist ein Laserprojektor installiert.
Der Laser tritt im Punkt aus dem Projektor aus. Während der Abendstunden wird u. a. eine gerade Linie
aus dem Projektor aus. Während der Abendstunden wird u. a. eine gerade Linie  auf die nördliche Seitenwand des Gebäudes projiziert, die durch die Seitenfläche
auf die nördliche Seitenwand des Gebäudes projiziert, die durch die Seitenfläche  beschrieben wird. Der Laserstrahl überstreicht in diesem Fall im Modell einen Teil der Ebene mit der Gleichung
beschrieben wird. Der Laserstrahl überstreicht in diesem Fall im Modell einen Teil der Ebene mit der Gleichung

Der Laser tritt im Punkt
2.4.1
Weise nach, dass der Punkt  in dieser Ebene liegt.
in dieser Ebene liegt.
(1 BE)
2.4.2
Ermittle die maximale Länge der Laserlinie 
(6 BE)
2.5
Eine Möwe fliegt unterhalb der schrägen Seitenwand, die westlich über das Wasser hinausragt. Die Punkte der Flugbahn dieser Möwe können im Modell zum jeweilligen Zeitpunkt  durch
durch
 mit
mit  beschrieben werden. Es gibt einen Zeitpunkt, zu dem die Möwe den kleinsten Abstand zu dieser Seitenwand hat
beschrieben werden. Es gibt einen Zeitpunkt, zu dem die Möwe den kleinsten Abstand zu dieser Seitenwand hat
Ermittle diesen Abstand.
Ermittle diesen Abstand.
(8 BE)
2.6
Für die Montage der Glasscheiben in den Außenwänden werden maschinell gefertigte Dichtungsgummis mit einer Qualitätsnorm von  verwendet.
verwendet.
Die Untersuchung einer großen Stichprobe aus der laufenden Produktion ergab, dass die Dichtungsgummis normalverteilt mit dem Erwartungswert und der Standardabweichung
und der Standardabweichung  sind.
Ermittle die Wahrscheinlichkeit, dass eine zufällig ausgewählte Gummidichtung der Norm entspricht.
sind.
Ermittle die Wahrscheinlichkeit, dass eine zufällig ausgewählte Gummidichtung der Norm entspricht.
Die Untersuchung einer großen Stichprobe aus der laufenden Produktion ergab, dass die Dichtungsgummis normalverteilt mit dem Erwartungswert
(3 BE)
2.1
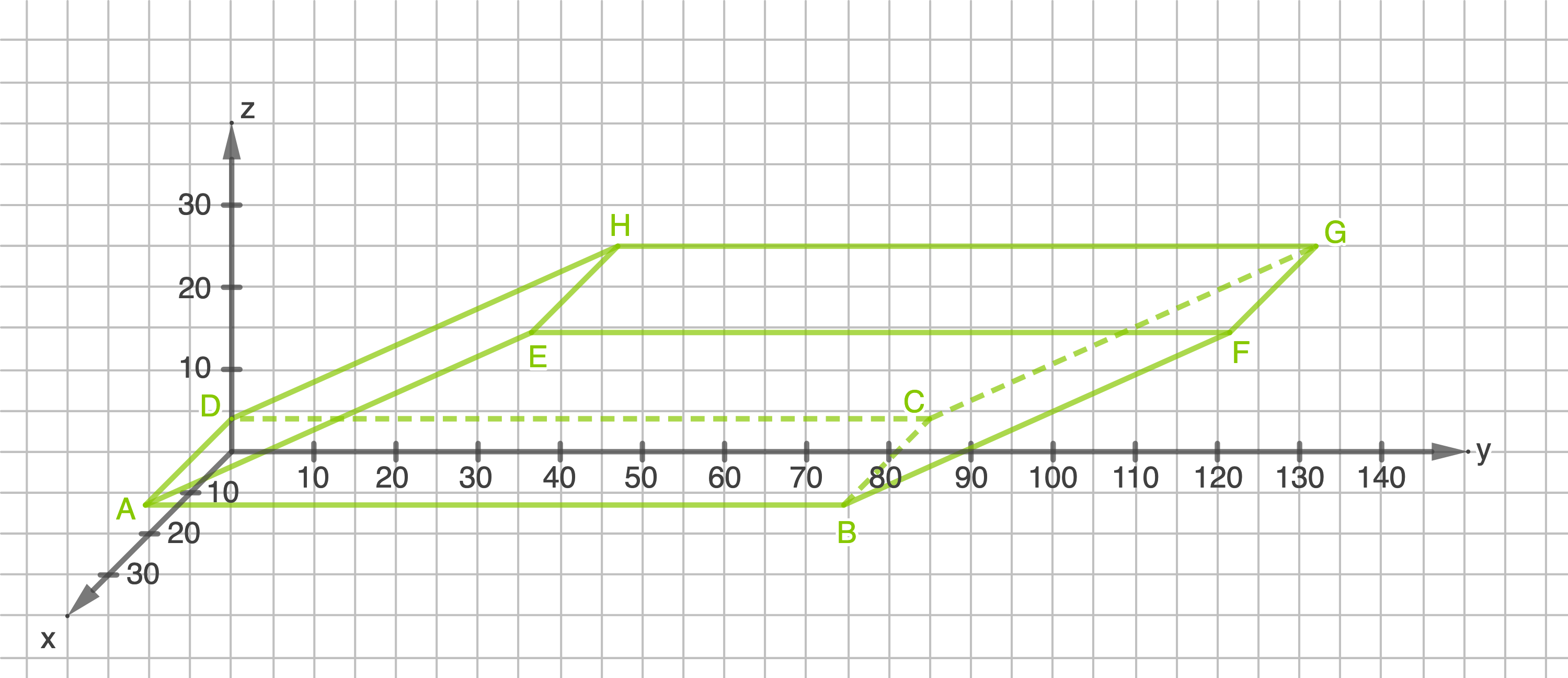
2.2
2.3
Normalenvektor:  Funktionsgleichung für den Ebenenterm:
Funktionsgleichung für den Ebenenterm:  Ebenengleichung:
Ebenengleichung: 


 Der Neigungswinkel der nicht lotrechten Seitenwände beträgt also
Der Neigungswinkel der nicht lotrechten Seitenwände beträgt also 
2.4.1
2.4.2
Paramtergleichung der Seitenfläche 
 mit
mit 

 Bestimmung der Schnittpunkte von
Bestimmung der Schnittpunkte von  mit den Kanten der Seitenfläche:
mit den Kanten der Seitenfläche:


 kein Schnittpunkt
kein Schnittpunkt
 kein Schnittpunkt
Länge der geraden Linie:
Länge
kein Schnittpunkt
Länge der geraden Linie:
Länge 
2.5
Abstand der Möwe zum Zeitpunkt  Ansatz für minimalen Abstand:
Ansatz für minimalen Abstand:  Abstand zu diesem Zeitpunkt:
Abstand zu diesem Zeitpunkt:  Abstand am Rand des Definitionsbereichs:
Abstand am Rand des Definitionsbereichs:  Da es laut Aufgabenstellung ein Minimum gibt, dieses nicht am Rand liegt und die Abstandsfunktion stetig ist, muss das Minimum bei
Da es laut Aufgabenstellung ein Minimum gibt, dieses nicht am Rand liegt und die Abstandsfunktion stetig ist, muss das Minimum bei  liegen. Der minimale Abstand beträgt also
liegen. Der minimale Abstand beträgt also 
2.6
Gesucht ist die Wahrscheinlichkeit, dass eine normalverteilte Zufallsgröße mit  und
und  einen Wert von 2,1 bis 2,3 annimmt. Mit der Verteilungsfunktion
einen Wert von 2,1 bis 2,3 annimmt. Mit der Verteilungsfunktion  ergibt sich diese Wahrscheinlichkeit als:
ergibt sich diese Wahrscheinlichkeit als:
