1. Analysis
Gegeben sind die in 
definierten Funktionen
mit 
sowie
.
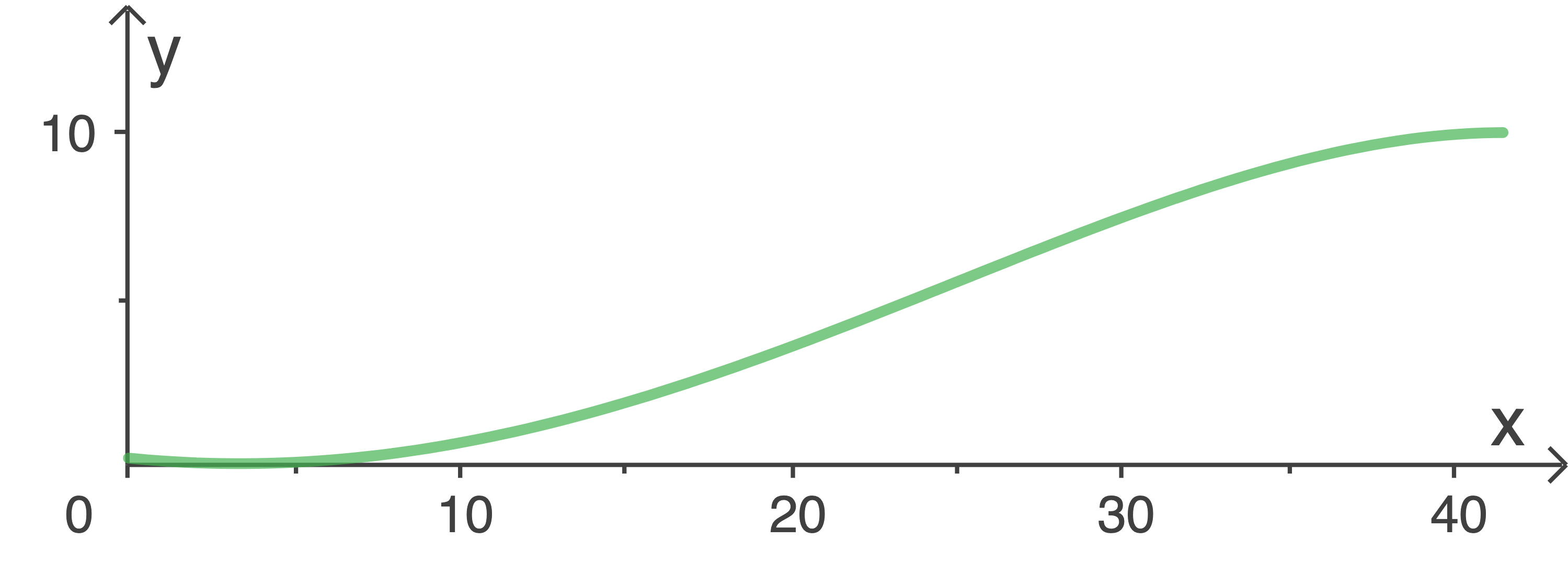
Die Abbildung 1 zeigt den Graphen von
.
Die Abbildung 1 zeigt den Graphen von
Abbildung 1
1.1
Berechne für den Graphen von 
die Koordinaten der Schnittpunkte mit den Koordinatenachsen sowie die Koordinaten des Extrempunkts. Zeichne den Graphen von in die Abbildung 1 ein.
(6 BE)
1.2
Gib an, für welche Werte von 
der Graph von oberhalb des Graphen von verläuft und für welche unterhalb.
Begründe deine Angabe.
Begründe deine Angabe.
(3 BE)
1.3
Für jeden Wert von 
gilt:
Die Funktionsterme von 
und 
unterscheiden sich nur um den Summanden 
.
Der Graph von hat genau zwei Wendepunkte, deren -Koordinaten 
und 
sind.
Gib an, was sich aus 
und 
hinsichtlich der Anzahl und der Lage der Wendepunkte des Graphen von im Vergleich zu den Wendepunkten des Graphen von folgern lässt.
Begründe deine Angabe ausgehend von und .
Begründe deine Angabe ausgehend von
(5 BE)
1.4
Die Tangente 
an den Graphen von im Punkt 
hat die Steigung 
, die Tangente 
an den Graphen von im Punkt 
die Steigung 
. Der Schnittpunkt dieser beiden Tangenten wird mit 
bezeichnet.
Die Piste ist in Querrichtung nicht geneigt und durchgehend
breit.
Die Profillinie wird für
modellhaft durch den Graphen der in definierten Funktion p(x) = ...
dargestellt.
Im verwendeten Koordinatensystem beschreibt die-Achse die Horizontale; eine Längeneinheit im Koordinatensystem entspricht 
m in der Realität.
1.4.1
Weise nach, dass für jeden Wert von auf der 
-Achse liegt.
(3 BE)
1.4.2
Die Gerade mit der Gleichung 
schneidet im Punkt 
und im Punkt 
.
Untersuche, für welche Werte von
das Dreieck 
rechtwinklig ist.
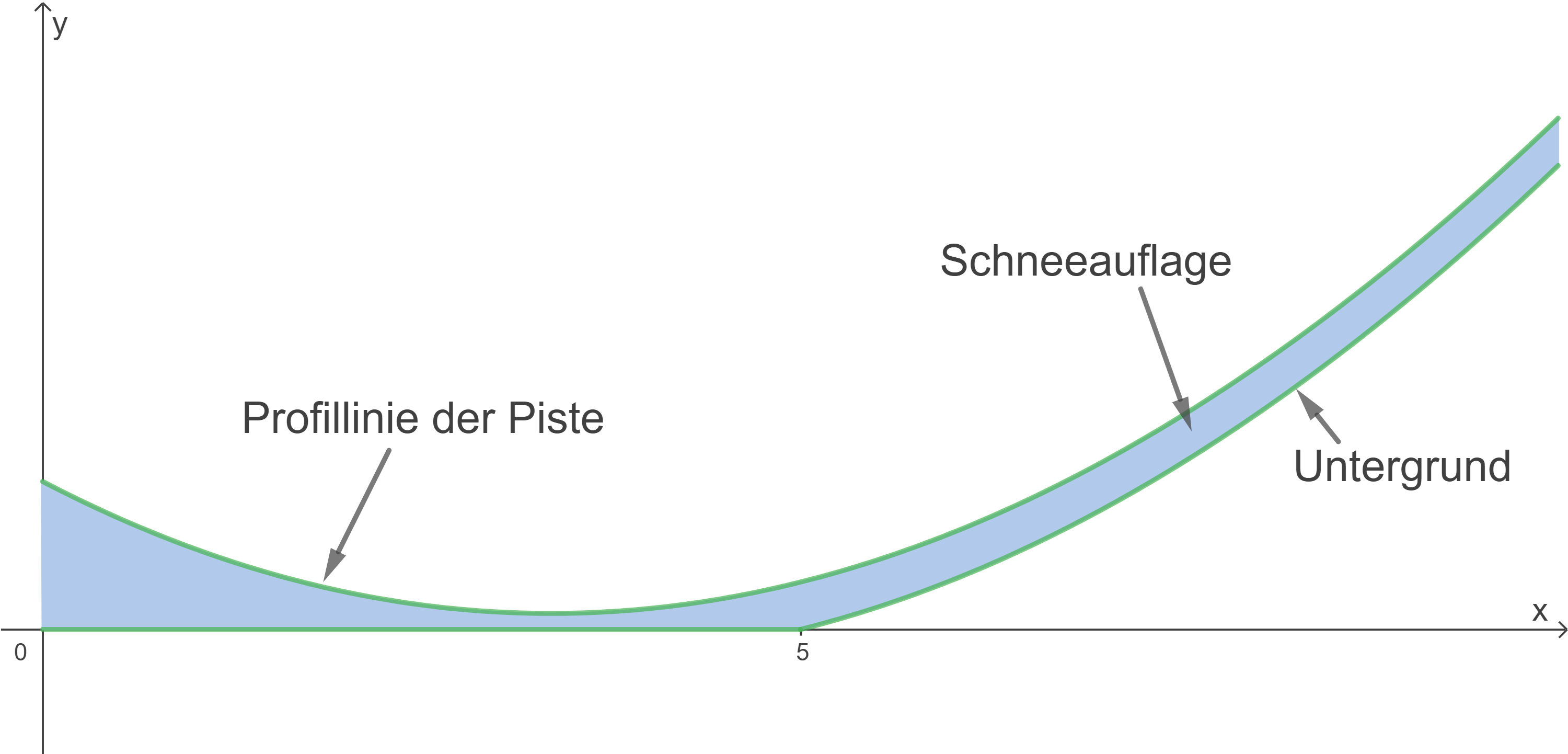
Die Abbildung 2 zeigt schematisch die Profillinie des Längsschnitts einer Skipiste in einer Skihalle.
Untersuche, für welche Werte von
(6 BE)
Die Piste ist in Querrichtung nicht geneigt und durchgehend
Die Profillinie wird für
Im verwendeten Koordinatensystem beschreibt die
1.5
Berechne die Größe des größten Neigungswinkels der Piste gegenüber der Horizontalen.
(4 BE)
1.6
Über der Piste verläuft in deren Längsrichtung ein Seil. Die beiden Enden des Seils werden im Modell durch 
und 
dargestellt; der Verlauf des Seils kann mithilfe einer in definierten Funktion 
mit 
, 
beschrieben werden.
1.6.1
Bestimme die Werte von und .
(zur Kontrolle: 
, 
)
(2 BE)
1.6.2
Untersuche, in welchen Bereichen der vertikale Abstand des Seils zur Piste mindestens 
m beträgt.
Ermittle die Höhendifferenz, um die die beiden Enden des Seils gemeinsam mindestens angehoben werden müssten, damit das Seil an jeder Stelle von der Piste einen vertikalen Abstand von mindestens 
hat.
(6 BE)
1.7
Die Abbildung 3 zeigt hellblau markiert die Schneeauflage im unteren Bereich der Piste; dazu wurde die Abbildung 2 in Richtung der -Achse stärker vergrößert als in Richtung der -Achse. Der Untergrund, auf dem der Schnee aufgebracht ist, wird für 
durch die -Achse dargestellt. Für den übrigen Teil der Piste soll davon ausgegangen werden, dass die in vertikaler Richtung gemessene Schneehöhe 
beträgt.
Bestimme das Volumen der Schneeauflage der gesamten Piste.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
1. Schritt: Koordinaten der Schnittpunkte mit den Koordinatenachsen von
Damit folgt, dass
ist. 
kann mit 
gelöst werden.
Damit sind 
und 
.
Somit sind die Schnittpunkte mit den Koordinatenachsen sind
und 
.
2. Schritt: Koordinaten des Extrempunkts
2.1. Schritt: Ableitungen von 
bestimmen.
![\(\begin{array}[t]{rlll}
f](https://mathjax.schullv.de/4bd87ef4877f4babb75d07239453bd01f5407ce8dcefcf6f5f443e17d48a201c?color=5a5a5a)
![\(\begin{array}[t]{rlll}
f](https://mathjax.schullv.de/1d9f661cd361febe908bf23025247756c9cbae019ed383a4dc566cc26ffc7495?color=5a5a5a)
2.2. Schritt: Notwendige Bedingung berechnen.
Damit folgt, dass
ist. kann mit 
gelöst werden.
Damit sind 
und 
.
2.3. Schritt: Hinreichende Bedingung für überprüfen.
Da die Hinreichende Bedingung
fordert, ist nur als Extrempunkt möglich.
Da
ist, handelt es sich um einen Hochpunkt.
2.4. Schritt: Koordinate des Extremums in einsetzen.
Der Extempunkt ist 
.
3. Schritt: Den Graph einzeichnen.
Damit folgt, dass
Vollständige Lösung anzeigen
Somit sind die Schnittpunkte mit den Koordinatenachsen sind
Damit folgt, dass
Da die Hinreichende Bedingung
Da
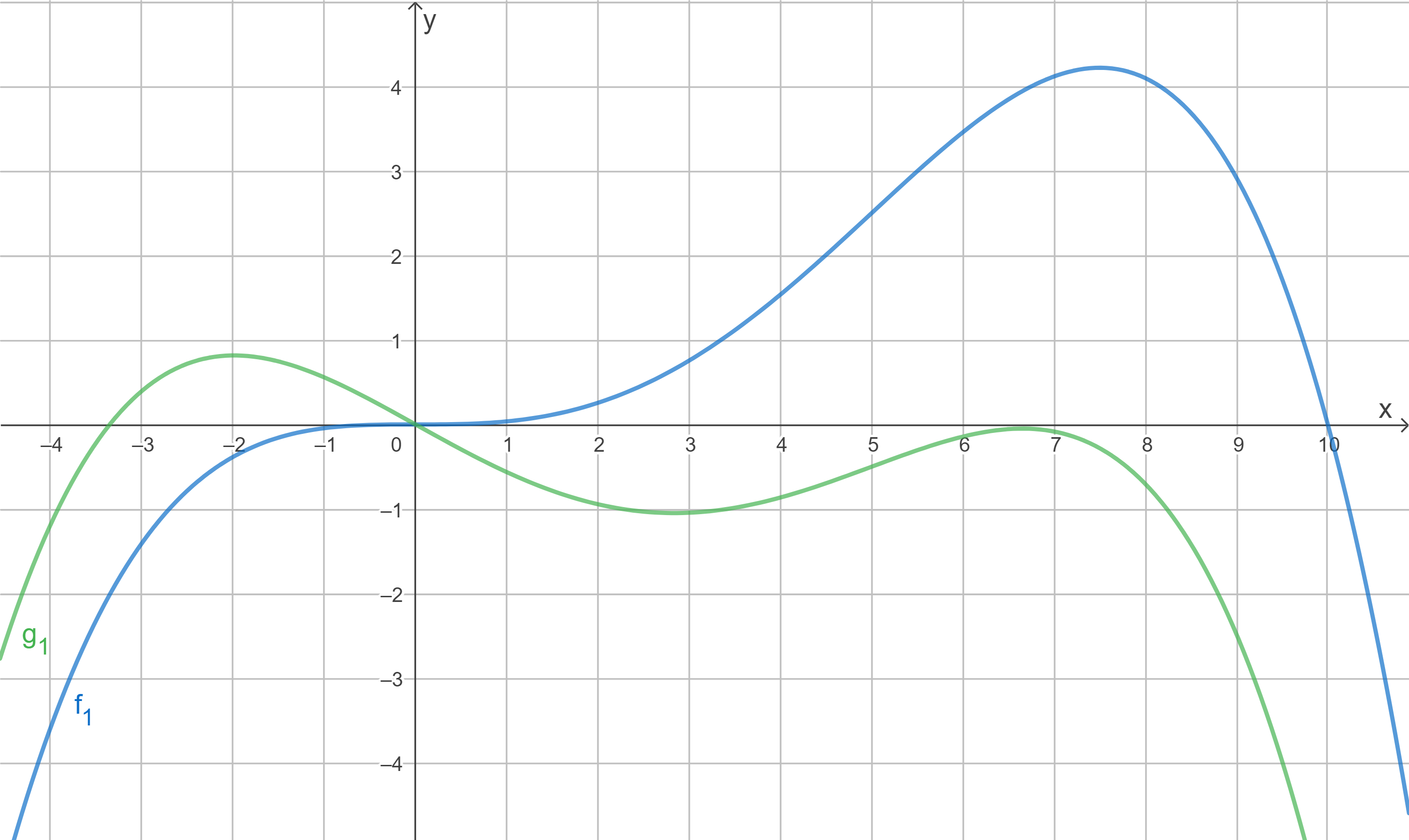
1.2
- Werte für
- bei
, da
gilt
- Werte für
- bei
gilt
1.3
- die gleich Anzahl von Wendepunkten
- die gleichen x-Koordinaten an ihren Wendepunkten
- die gleiche y-Koordinate bei
- durch
- durch
- der Graph von
- die x-Koordinaten der Wendepunkte sind
- durch
haben
die gleiche y-Koordinate
1.4.1
1. Schritt: Tangentengleichungen bestimmen.
1.1 Schritt: Tangentengleichung bestimmen.
Bekannt ist: bestimmen:
wird somit durch 
beschrieben.
1.2 Schritt: Tangentengleichungen bestimmen.
Bekannt ist: bestimmen:
Somit wird durch 
beschrieben
2. Schritt: Schnittpunkt bestimmen.
2.1. Schritt: Tangentengleichungen gleichsetzen.
2.2. Schritt: y-Koordinate bestimmen.
Da der Schnittpunkt auf beiden Tangenten liegt, kannst du die x-Koordinate in eine der Tangentengleichungen einsetzen, um die die y-Koordinate zu bestimmen.
![\(\begin{array}[t]{rlll}
y&=&\frac{1}{a^2}\cdot 0-\frac{5}{2a^3} & \quad \scriptsize \\[5pt]
y&=&-\frac{5}{2a^3} & \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/bfefc6753f891f06389053fa2178e3c9122bab8cd36b788265eac8f002e8391b?color=5a5a5a)
Beide Tangenten schneiden die y-Achse bei 
.
3. Schritt: Begründen warum immer auf der y-Achse liegt.
. liegt deshalb für alle Werte von auf der y-Achse.
Bekannt ist:
1.2 Schritt: Tangentengleichungen
Bekannt ist:
Somit wird
2.2. Schritt: y-Koordinate bestimmen.
Da der Schnittpunkt auf beiden Tangenten liegt, kannst du die x-Koordinate
3. Schritt: Begründen warum
- Wenn
geht, ist
ist zu vernachlässigen, da die
enthalten ist und
gilt.
- Wenn
geht, ist
1.4.2
1. Schritt: Schlussfolgern, wo der rechte Winkel liegen muss.
Da für gilt 
für 
, kann im Eckpunkt kein rechter Winkel liegen.
Da
für ist, kann im Eckpunkt ebenfalls kein rechter Winkel liegen.
Der rechte Winkel muss somit im Eckpunkt liegen.
2. Schritt: Bedingung für den rechten Winkel aufstellen und nach auflösen.
Da ist, muss positiv sein. Somit ist das Dreieck für 
rechtwinklig.
Da für
Da
Der rechte Winkel muss somit im Eckpunkt
Da
1.5
1. Schritt: Die ersten beiden Ableitungen von 
bilden.
2. Schritt: Koordinaten des größten Neigungswinkels bestimmen.
Der größte Neigungswinkel ist an der Stelle, an der die Funktion der Steigung (also die erste Ableitung) einen Extrempunkt hat. Es muss also
als hinreichende Bedingung gelten.
Da 
gilt, ist die x-Koordinate der größten Steigung 
.
3. Schritt: Winkel berechnen.
Damit ist der Winkel zwischen dem größten Neigungswinkel der Piste und der Horizontalen
.
2. Schritt: Koordinaten des größten Neigungswinkels bestimmen.
Der größte Neigungswinkel ist an der Stelle, an der die Funktion der Steigung (also die erste Ableitung) einen Extrempunkt hat. Es muss also
Damit ist der Winkel zwischen dem größten Neigungswinkel der Piste und der Horizontalen
1.6.1
1. Schritt: Punkte einsetzen und Gleichungen aufstellen.
in 
einsetzen:
in einsetzen:
2. Schritt: Gleichungen gleichsetzen.
3. Schritt: in eine derGleichungen einsetzen.
Damit ist
.
3. Schritt:
Damit ist
1.6.2
1. Schritt: Untersuchen welche Bereiche des Seils einen vertikalen Abstand von m haben.
1.1 Schritt: Funktion des Abstands von Seil zu Piste aufstellen.
1.2 Schritt: Die Bereiche mit
nummerisch ermitteln.
Um die Bereiche zu finden, an welchen das Seil
m über der Piste hängt, musst du 
setzen und für den Bereich zwischen den Aufhängepunkten berechnen. Als Bereich ergibt sich so 
.
Die Gleichung lässt sich nummerisch mit einem CAS System lösen.
TI nspire CAS
Casio Classpad II
Die Gleichung ist für die Bereiche 
mit 
und 
mit 
erfüllt.
2. Schritt: Ermitteln wie tief das Seil, an der tiefsten Stelle, im Bereich 
, über der Piste hängt.
2.1. Schritt: Erste Ableitung von 
bilden.
TI nspire CAS
Casio Classpad II
Die Ableitung ist:
2.2. Schritt: Hinreichende Bedingung, im Bereich , nummerisch lösen.
TI nspire CAS
Casio Classpad II
Aus 
für den Bereich
folgt 
als x-Koordinate des Tiefpunkts.
Damit folgt:
3. Schritt: Ermitteln wieviel das Seil, an den Endpunkten, angehoben werden muss.
Der tiefste Punkt muss um
angehoben werden.
![\(\begin{array}[t]{rlll}
0,3- d(x_3) & = & 0,3-0,1911 & \quad \scriptsize \\[5pt]
& \approx& 0,1089 & \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f5fa216fdd23ecd286cff12b1965962afbfddef0e9783e3b58260a855a0e479b?color=5a5a5a)
Die Seilenden müssen um etwa 
, also 
m angehoben werden.
1.2 Schritt: Die Bereiche mit
Um die Bereiche zu finden, an welchen das Seil
Die Gleichung
menu 
3: Algebra 7
keyboard Math1 
menu 4: Analysis 1: Ableitung
keyboard Math2 
menu 3: Algebra 7
keyboard Math1
für den Bereich
Damit folgt:
3. Schritt: Ermitteln wieviel das Seil, an den Endpunkten, angehoben werden muss.
Der tiefste Punkt muss um
1.7
Das Volumen der Schneeauflage berechnet sich aus dem Integral der Profillinie und der Breite der Piste (
m). Im hinteren Integral kürzt sich die Funktion raus. Das vordere Integral kannst du integrieren, indem du es in Einzelintegrale zerlegst.
Die Schneeauflage hat ein Volumen von
m
.
Die Schneeauflage hat ein Volumen von