3. Stochastik

Ein Unternehmen produziert Stahlkugeln für Kugellager. Erfahrungsgemäß sind $4\;\%$ aller Kugeln fehlerhaft. $800$ Kugeln werden zufällig ausgewählt. Die Anzahl der fehlerhaften Kugeln unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße beschrieben werden.

3.1

Bestimme die Wahrscheinlichkeit dafür, dass unter den ausgewählten Kugeln weniger als $30$ fehlerhaft sind.

(2 BE)

3.2

Bestimme die Wahrscheinlichkeit dafür, dass die Anzahl der fehlerhaften Kugeln unter den ausgewählten höchstens um eine halbe Standardabweichung vom Erwartungswert dieser Anzahl abweicht.

(5 BE)

3.3

Eine fehlerhafte Kugel ist entweder zu klein oder zu groß. Die Wahrscheinlichkeit dafür, dass eine Kugel einen zu klein ist, beträgt $3\;\%$ .
Alle Kugeln werden vor dem Verpacken geprüft. Dabei werden $95\;\%$ der zu kleinen Kugeln, $98 \;\%$ der zu großen Kugeln, aber auch $0,5\;\%$ der Kugeln ohne Fehler aussortiert.

3.3.1

Stelle den Sachzusammenhang in einem beschrifteten Baumdiagramm dar.

(4 BE)

3.3.2

Berechne die Wahrscheinlichkeit dafür, dass eine aussortierte Kugel nicht zu klein ist.

(3 BE)

3.4

Die Kugeln werden in Packungen verkauft. Ein Teil der verkauften Packungen wird zurückgegeben. Die Wahrscheinlichkeit dafür, dass eine verkaufte Packung zurückgegeben wird, beträgt $3 \;\%$ . Dem Unternehmen entsteht pro Packung, die zurückgegeben wird, ein Verlust von $5,80\; €$ ; pro Packung, die nicht zurückgegeben wird, erziehlt das Unternehmen einen Gewinn von $8,30 \;€$ .

Bestimme die Wahrscheinlichkeit, mit der das Unternehmen bei einem Verkauf von $200$ Packungen einen Gesamtgewinn von mindestens $1500\;€$ erziehlt.

(4 BE)

3.5

Ein Konkurrenzunternehmen stellt ebenfalls Stahlkugeln für Kugellager her. Beide Unternehmen bieten Kugeln mit einem Durchmesser von $6\; \text{mm}$ (Normwert) und einer Toleranz von $0,01\; \text{mm}$ zum Kauf an. Die Einhaltung dieses Normwertes wird im Rahmen einer Stichprobe untersucht. Dazu wurden in den Unternehmen jeweils $10\,000$ Kugeln aus einer Tagesproduktion entnommen und deren Durchmesser gemessen. Die Tabelle zeigt die dabei ermittelten Werte.

Tabelle anzeigen

Durchmesser in mm	Häufigkeit im Unternehmen	Häufigkeit im Konkurrenzunternehmen
$5,97$	$3$	$4$
$5,98$	$12$	$2$
$5,99$	$257$	$1633$
$6$	$7896$	$6301$
$6,01$	$1830$	$2052$
$6,02$	$2$	$7$
$6,03$	$0$	$1$

3.5.1

Werte diese statistische Erhebung durch einen geeigneten Mittelwert und ein geeignetes Streumaß aus.

(4 BE)

3.5.2

Beurteile die Qualität der Kugeln beider Unternehmen.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

3.1

$B\left(n;p;X\right)=B\left(800;\frac{4}{100};X\lt30\right)=B\left(800;\frac{4}{100};X\leq29\right)$
X: Anzahl der fehlerhaften Kugeln

$P_{0,04}^{800}(X\leq29) \approx 33\%$

Vollständige Lösung anzeigen

$P_{0,04}^{800}(X\lt30)\approx 33\%$

3.2

1. Schritt: Erwartungswert und halbe Standardabweichung bestimmen.
Der Erwartungswert ist: $n \cdot p= 800 \cdot0,04=32$
Die Standardabweichung ist: $\sqrt{n \cdot p \cdot (1-p)}$
Daraus folgt für die halbe Standardabweichung: $0,5 \cdot \sqrt{800 \cdot 0,04 \cdot 0,96} \approx 2,8$

2. Schritt: Wahrscheinlichkeit bestimmen

$P_{0,04}^{800}(30\leq X\leq34) \approx 35\%$

Vollständige Lösung anzeigen

3.3.1

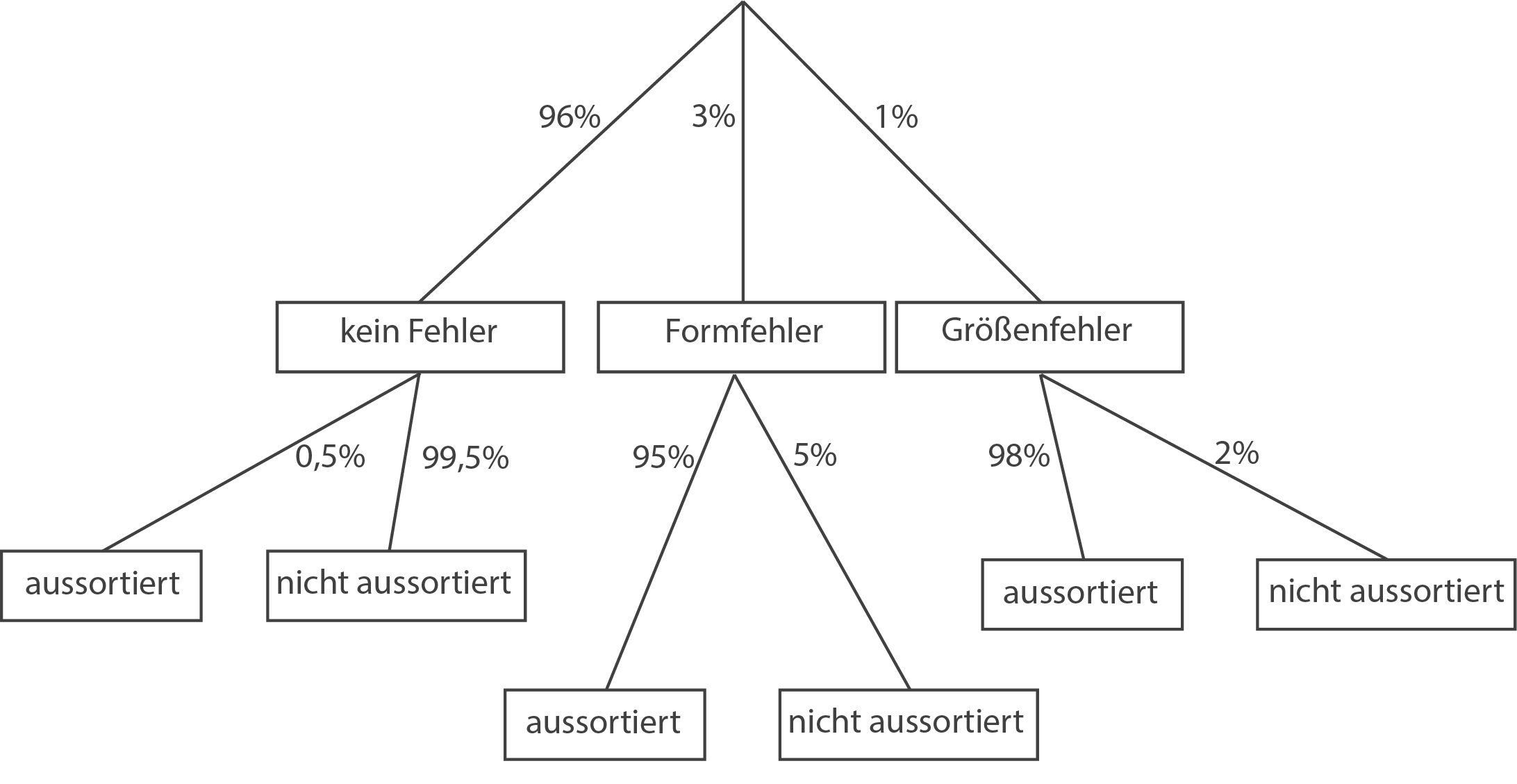
Diagramm zur Fehleranalyse mit Kategorien und Prozentangaben.

3.3.2

Eine Kugel hat entweder einen Formfehler, einen Größenfehler oder keinen Fehler. Deshalb werden die Wahrscheinlichkeiten, dass sie entweder keinen Fehler oder einen Größenfehler hat addiert und durch die Wahrscheinlichkeit, dass sie einen Fehler hat, geteilt.

$\frac{0,01 \cdot 0,98+0,96 \cdot 0,005}{0,03 \cdot 0,95+0,01\cdot0,98+0,96\cdot0,005}\approx 34\%$

3.4

$z$ beschreibt die Anzahl der zurückgegebenen Packungen.

$z \leq 11,35$

Vollständige Lösung anzeigen

$Z$ beschreibt die Zufallsgröße der zurückgegebenen Packungen.

$P_{0,03}^{200}(Z\leq 11)\approx 98\%$

Vollständige Lösung anzeigen

3.5.1

1. Schritt: Wertung der Erhebung des Unternehmens.
1.1 Schritt: Mittelwert bestimmen.

$\overline{x} \approx 6001,5$

Vollständige Lösung anzeigen

1.2 Schritt: Streumaß bestimmen.
$\begin{array}[t]{rll} \sigma_x&=& \sqrt{\sum\limits^8_{i=1}\left(x_i-6001,5\right)^2} & \quad \scriptsize \\[5pt] &\approx& 4,4 \mu m & \quad \scriptsize \\[5pt] \end{array}$

2. Schritt: Wertung der Erhebung des Konkurrenzunternehmens.
2.1 Schritt: Mittelwert bestimmen.

$\overline{x} \approx 6000,4 \mu m$

Vollständige Lösung anzeigen

2.2 Schritt:Streumaß bestimmen.
$\begin{array}[t]{rll} \sigma_x&=& \sqrt{\sum\limits^8_{i=1}\left(x_i-6000,4\right)^2} & \quad \scriptsize \\[5pt] &\approx& 6,1 \mu m & \quad \scriptsize \\[5pt] \end{array}$

3.5.2

die Mittelwerte weichen beide nur gering vom Normwert ab
der Mittelwert des Konkourrenzunternehmen weicht etwas weniger vom Normwert ab
das Konkurrenzunternehmen hat eine höhere Standardabweichung

es weichen mehr Kugeln vom Normwert ab

beim Unternehmen liegen $1,7$ ‰ außerhalb des Toleranzbereichs
beim Konkurrenzunternehmen liegen $1,4$ ‰ außerhalb des Toleranzbereichs

Daraus folgt, dass das Konkurrenzunternehmen zu bevorzugen ist, wenn die Kugeln möglichst nah am Normwert sein sollen. In allen anderen Fällen ist das Unternehmen zu bevorzugen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?