3 Stochastik
3.1
Eine Schokoladenfabrik stellt Pralinen mit mehreren gleichartigen Maschinen her. Zum Firmenjubiläum erhalten einige dieser Pralinen eine Prägung. Der Anteil der Pralinen mit Prägung an der gesamten Produktion beträgt  Alle Pralinen werden gemischt und in Packungen zu je
Alle Pralinen werden gemischt und in Packungen zu je  Stück verpackt. Eine Packung wird zufällig der laufenden Produktion entnommen. Die Zufallsgröße
Stück verpackt. Eine Packung wird zufällig der laufenden Produktion entnommen. Die Zufallsgröße  gibt die Anzahl der Pralinen mit Prägung in dieser Packung an.
Eine der folgenden Abbildungen stellt die Verteilung der Zufallsgröße
gibt die Anzahl der Pralinen mit Prägung in dieser Packung an.
Eine der folgenden Abbildungen stellt die Verteilung der Zufallsgröße  dar.
dar.
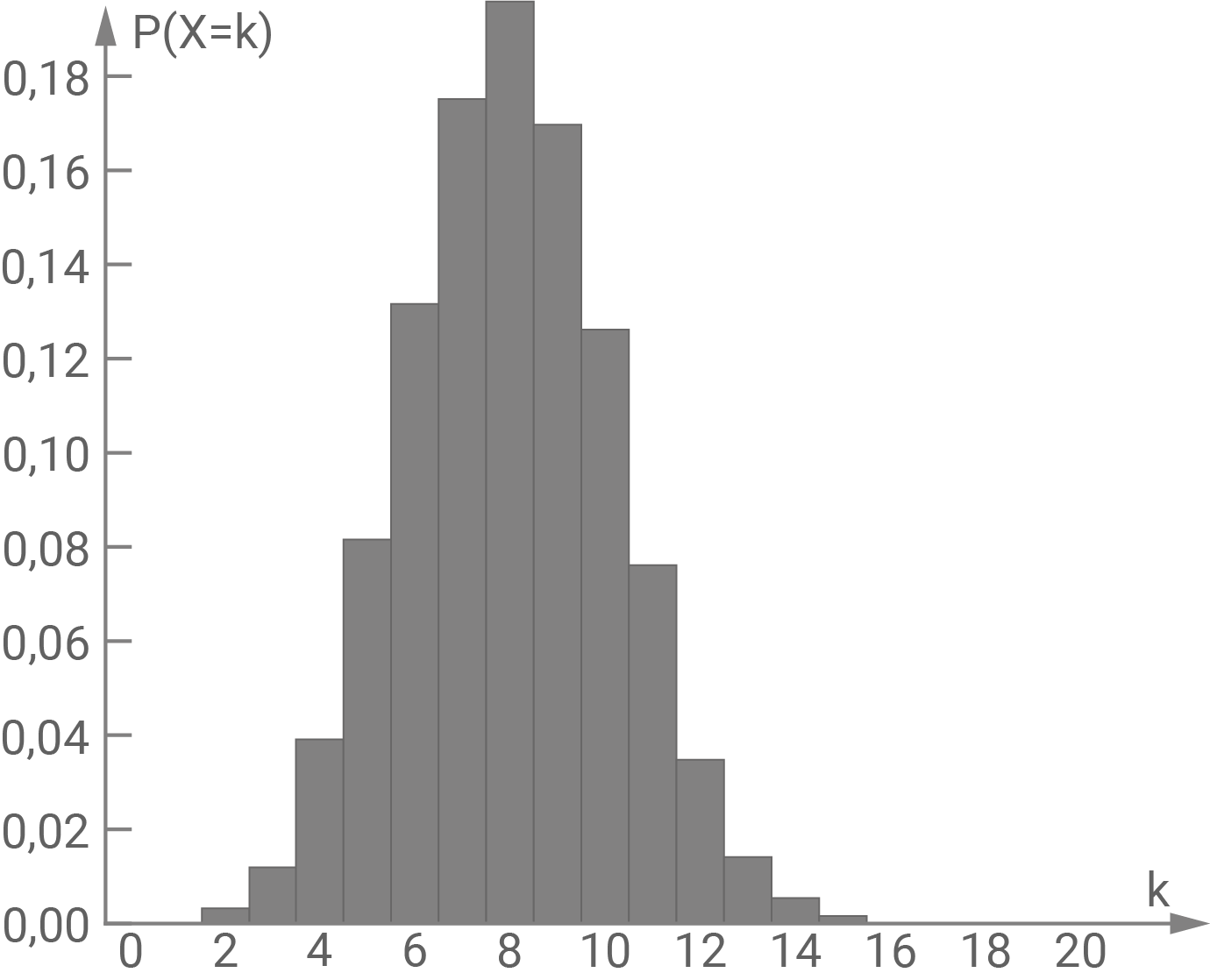
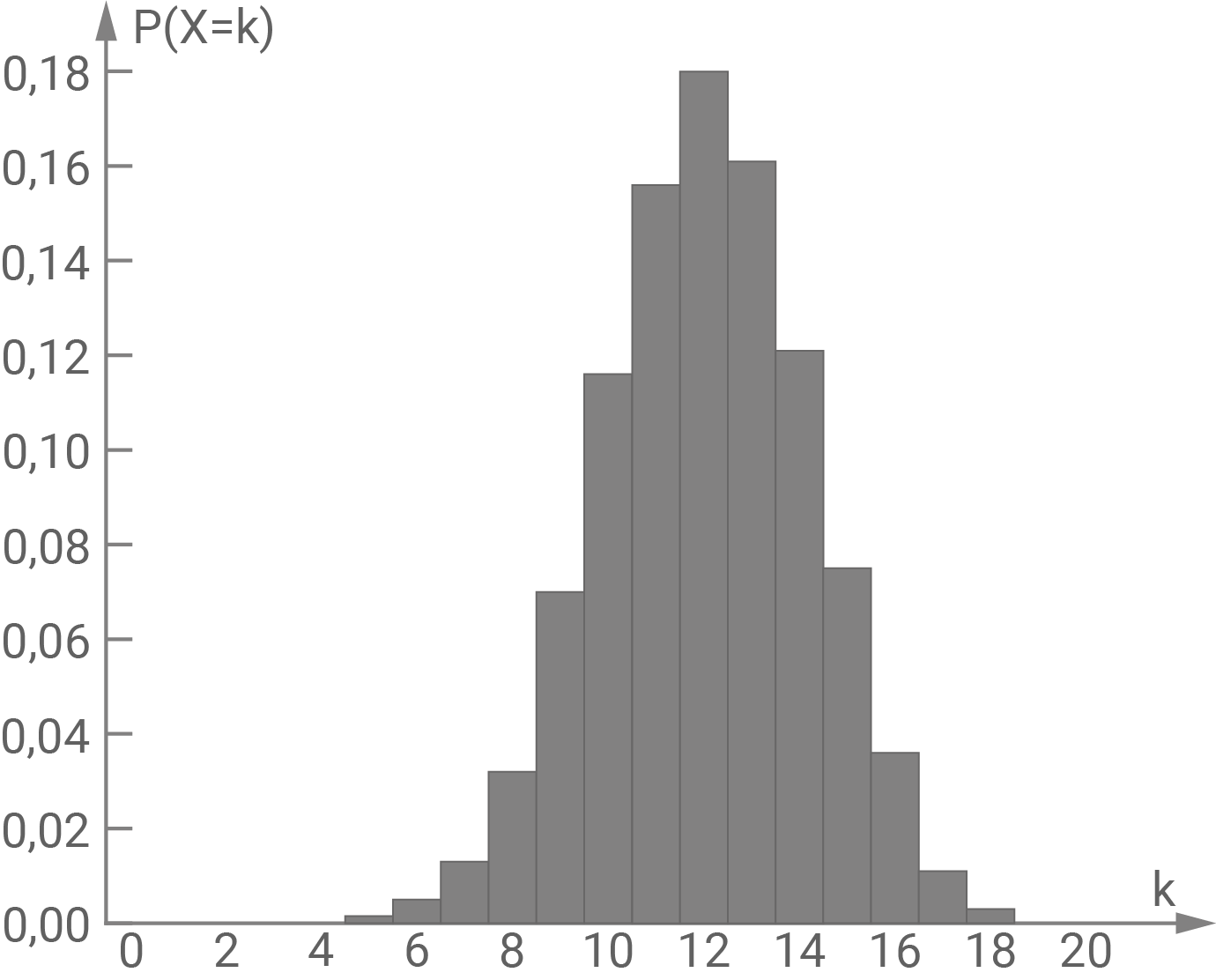

Abbildung I

Abbildung II
3.1.1
Begründe, dass die Binomialverteilung dafür geeignet ist, Vorhersagen zu diesem Vorgang zu treffen.
(2 BE)
3.1.2
Gib an, welche der beiden Abbildungen die Verteilung von  darstellt. Begründe deine Entscheidung.
darstellt. Begründe deine Entscheidung.
Für ein Schulfest werden
(2 BE)
3.1.3
Mit dem Erwartungswert  und der Standardabweichung
und der Standardabweichung  von
von  ist der folgende Term zur Berechnung der Wahrscheinlichkeit eines Ereignisses gegeben:
ist der folgende Term zur Berechnung der Wahrscheinlichkeit eines Ereignisses gegeben:
 Ermittle für
Ermittle für  die möglichen Werte von
die möglichen Werte von  die zu diesem Ereignis gehören.
die zu diesem Ereignis gehören.
(4 BE)
3.1.4
Mit einer Wahrscheinlichkeit von mindestens  sollen auf jedem Teller wenigstens 3 Pralinen mit Prägung liegen.
Ermittle unter Beachtung dieser Bedingung die größtmögliche Anzahl der Teller auf diesem Schulfest.
sollen auf jedem Teller wenigstens 3 Pralinen mit Prägung liegen.
Ermittle unter Beachtung dieser Bedingung die größtmögliche Anzahl der Teller auf diesem Schulfest.
(5 BE)
3.2
Eine andere Produktionslinie dieser Schokoladenfabrik stellt kugelförmige Pralinen aus dunkler Schokolade und aus heller Schokolade her. Pralinen beider Schokoladenarten können eine Füllung enthalten. Unter allen kugelförmigen Pralinen sind drei Viertel aus dunkler Schokolade, davon wiederum enthalten  eine Füllung.
Aus der gesamten Produktion kugelförmiger Pralinen wird eine zufällig entnommen. Folgende Ereignisse werden untersucht:
eine Füllung.
Aus der gesamten Produktion kugelförmiger Pralinen wird eine zufällig entnommen. Folgende Ereignisse werden untersucht:

: „Die Praline ist aus dunkler Schokolade.“
: „Die Praline enthält eine Füllung.“
3.2.1
Zeige, dass  gilt.
gilt.
(1 BE)
3.2.2
Interpretiere die Gleichung  im Sachzusammenhang.
im Sachzusammenhang.
(2 BE)
3.2.3
Stelle diesen Sachverhalt in einer Vierfeldertafel oder in einem Baumdiagramm dar.
(2 BE)
3.2.4
Bestimme die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Praline entweder eine gefüllte Praline aus heller Schokolade ist oder eine ungefüllte aus dunkler Schokolade.
(2 BE)
3.2.5
Eine zufällig ausgewählte Praline ist ungefüllt. Ermittle die Wahrscheinlichkeit dafür, dass es sich um eine Praline aus heller Schokolade handelt.
(2 BE)
3.2.6
Die Pralinen aus dunkler Schokolade haben  verschiedene Füllungen, die Pralinen aus heller Schokolade haben
verschiedene Füllungen, die Pralinen aus heller Schokolade haben  verschiedene Füllungen. Die gefüllten Pralinen werden in Tüten verpackt, jede Tüte enthält
verschiedene Füllungen. Die gefüllten Pralinen werden in Tüten verpackt, jede Tüte enthält  Pralinen. In einer Tüte sind sowohl Pralinen aus dunkler Schokolade mit mindestens
Pralinen. In einer Tüte sind sowohl Pralinen aus dunkler Schokolade mit mindestens  verschiedenen Füllungen als auch Pralinen mit heller Schokolade, ebenfalls mit mindestens
verschiedenen Füllungen als auch Pralinen mit heller Schokolade, ebenfalls mit mindestens  verschiedenen Füllungen. Keine Pralinensorte ist mehrfach in einer Tüte enthalten.
Ermittle die Anzahl der Möglichkeiten, diese Pralinentüten zu füllen.
verschiedenen Füllungen. Keine Pralinensorte ist mehrfach in einer Tüte enthalten.
Ermittle die Anzahl der Möglichkeiten, diese Pralinentüten zu füllen.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1.1
Bei jeder Praline wird geprüft, ob sie eine Prägung hat oder nicht. Da die zu untersuchenden  Pralinen aus einer sehr großen Anzahl hergestellter Pralinen zufällig ausgewählt wurden, kann davon ausgegangen werden, dass die Wahrscheinlichkeit für eine Praline mit Prägung bei jeder einzelnen Prüfung gleich groß ist.
Pralinen aus einer sehr großen Anzahl hergestellter Pralinen zufällig ausgewählt wurden, kann davon ausgegangen werden, dass die Wahrscheinlichkeit für eine Praline mit Prägung bei jeder einzelnen Prüfung gleich groß ist.
3.1.2
Erwartungswert von  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
E(X) &=& 20 \cdot 0,6 \\[5pt]
&=& 12
\end{array}\)](https://mathjax.schullv.de/70d2f7358a4c701d402da8e00a8b3beaf397115d0805c88c15ad567a4d9867d7?color=5a5a5a) Die Abbildung II stellt die beschriebene Zufallsgröße dar. In der Abbildung I ist die höchste Säule bei
Die Abbildung II stellt die beschriebene Zufallsgröße dar. In der Abbildung I ist die höchste Säule bei  nicht beim Erwartungswert
nicht beim Erwartungswert 
3.1.3
Erwartungswert von  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
E(Y)&=& 10 \cdot 20 \cdot 0,6 \\[5pt]
&=&120
\end{array}\)](https://mathjax.schullv.de/09720eba5761a441f92bf18390583695e92b4e7097cd1063fb4b4abe2819205b?color=5a5a5a) Standardabweichung von
Standardabweichung von  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
s &=& \sqrt{200 \cdot 0,6 \cdot 0,4} \\[5pt]
& \approx& 6,93
\end{array}\)](https://mathjax.schullv.de/f21c5b3dc3b532dc6664f7b89f5c3ca3117b1a7b5b25fae4f18832a7313a9d66?color=5a5a5a) Dann gilt:
Dann gilt:
 Die möglichen Werte sind
Die möglichen Werte sind 
3.1.4
Es wird die kleinstmögliche Anzahl an Pralinen pro Teller berechnet.
Mit dem WTR ergeben sich folgende Wahrscheinlichkeiten:![\(\begin{array}[t]{rll}
P_{0,6}^8(X \geq 3)&=& 1-P_{0,6}^8(X \leq 2)&\\[5pt]
&\approx& 95,02 \,\%
\end{array}\)](https://mathjax.schullv.de/9adcc41d78b358f0be38240383dc6d41e9b93047aa5bb2ca03f921e72e31797a?color=5a5a5a)
![\(\begin{array}[t]{rll}
P_{0,6}^7(X \geq 3)&=& 1-P_{0,6}^7(X \leq 2)&\\[5pt]
&\approx& 90,37 \,\%
\end{array}\)](https://mathjax.schullv.de/1142fb7ca54170c9cab492322624bd2e04d180758a45a917b3fce6f7d2c1e753?color=5a5a5a) Auf einen Teller müssen somit mindestens
Auf einen Teller müssen somit mindestens  Pralinen gelegt werden. Da
Pralinen gelegt werden. Da  , beträgt die größtmögliche Anzahl der Teller
, beträgt die größtmögliche Anzahl der Teller 
Mit dem WTR ergeben sich folgende Wahrscheinlichkeiten:
3.2.1
3.2.2
Die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Praline aus heller Schokolade und ungefüllt ist, beträgt  .
.
3.2.3
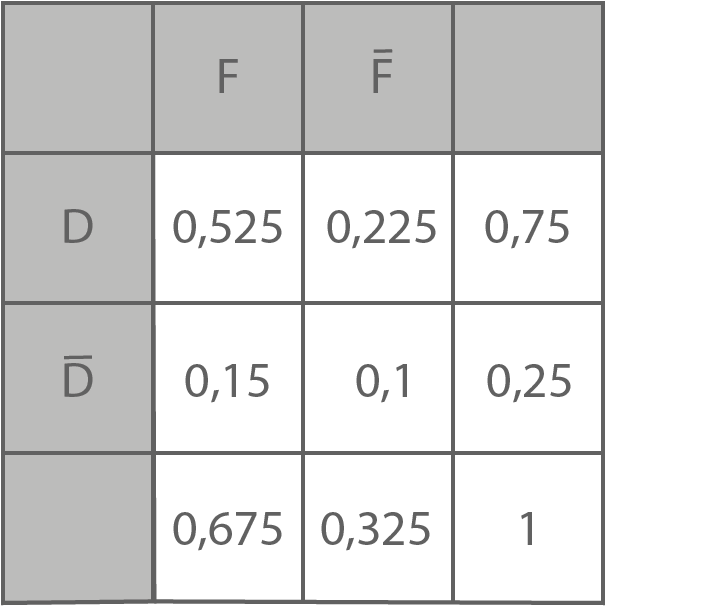
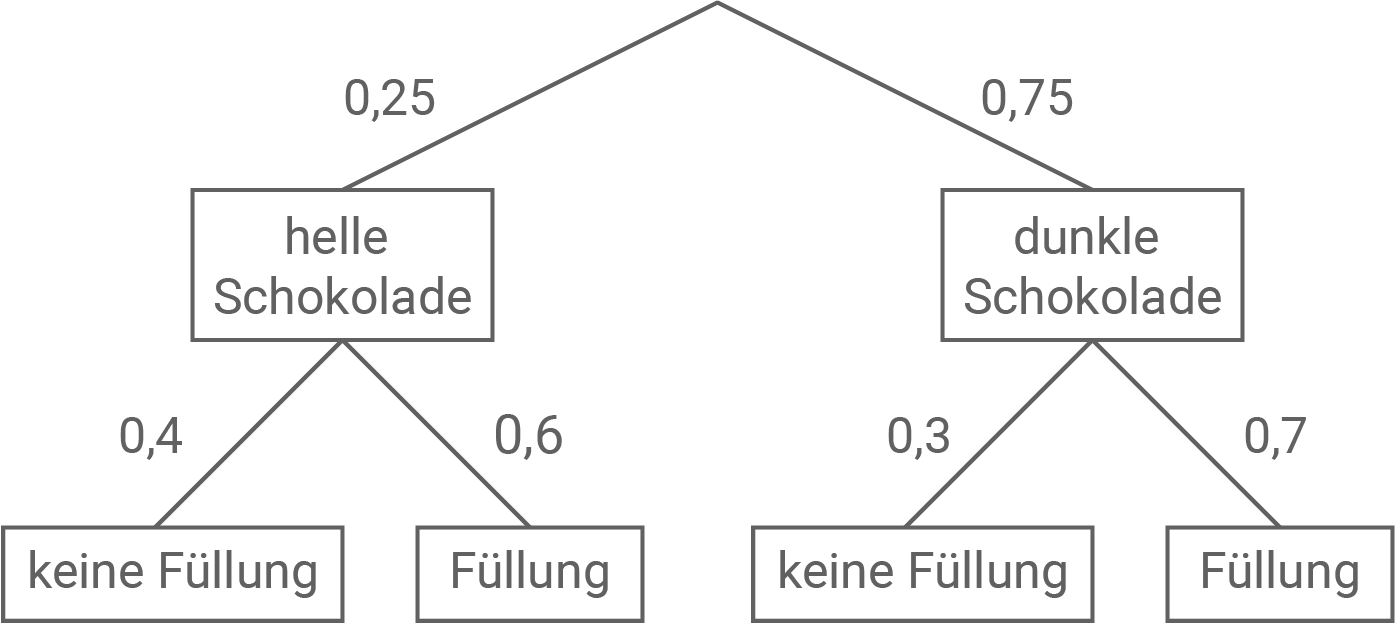
3.2.4
3.2.5
3.2.6
Da in jeder Tüte mindestens  Pralinen mit heller als auch
Pralinen mit heller als auch  Pralinen mit dunkler Schokolade sind und sich insgesamt
Pralinen mit dunkler Schokolade sind und sich insgesamt  Pralinen in einer Tüte befinden, gibt es in jeder Tüte entweder
Pralinen in einer Tüte befinden, gibt es in jeder Tüte entweder  Pralinen mit heller und
Pralinen mit heller und  mit dunkler Schokolade oder
mit dunkler Schokolade oder  Pralinen mit heller und
Pralinen mit heller und  mit dunkler Schokolade.
mit dunkler Schokolade.
Die Pralinen mit dunkler Schokolade haben alle eine unterschiedliche Füllung. Da es insgesamt verschiedene Füllungen der dunklen Pralinen gibt, gibt es je nach Tüte
verschiedene Füllungen der dunklen Pralinen gibt, gibt es je nach Tüte  beziehungsweise
beziehungsweise  Möglichkeiten die Pralinen mit dunkler Schokolade zu wählen.
Möglichkeiten die Pralinen mit dunkler Schokolade zu wählen.
Auch die Pralinen mit heller Schokolade haben alle eine unterschiedliche Füllung. Da es insgesamt verschiedene Füllungen der hellen Pralinen gibt, gibt es je nach Tüte
verschiedene Füllungen der hellen Pralinen gibt, gibt es je nach Tüte  beziehungsweise
beziehungsweise  Möglichkeiten die Pralinen mit heller Schokolade zu wählen.
Insgesamt ergibt sich:
Möglichkeiten die Pralinen mit heller Schokolade zu wählen.
Insgesamt ergibt sich:
 Es gibt 980 Möglichkeiten die Pralinentüten zu füllen.
Es gibt 980 Möglichkeiten die Pralinentüten zu füllen.
Die Pralinen mit dunkler Schokolade haben alle eine unterschiedliche Füllung. Da es insgesamt
Auch die Pralinen mit heller Schokolade haben alle eine unterschiedliche Füllung. Da es insgesamt