1 Analysis – Pflichtaufgabe

Für einen Spielplatz wird eine Sitzgelegenheit mit einem besonderen Design geplant. Der Querschnitt ihrer Oberfläche wird durch den Graphen der in $\mathbb{R}$ definierten Funktion $q$ mit $q(x)=\dfrac{1}{1600} \cdot x^5-\dfrac{1}{25} \cdot x^3+x$ im Intervall $-7 \leq x \leq 8$ modelliert.

Der Boden verläuft entlang der Gerade $y=-5$ . Die Längeneinheit ist $1\,\text{dm}.$

Die Abbildung 1 zeigt den Querschnitt der Sitzgelegenheit. Die Sitzgelegenheit verfügt über einen unteren und einen oberen Sitzbereich.

Die Extrempunkte des Graphen von $q$ heißen $H_u, T_u, H_o, T_o$ und sind in der Abbildung eingezeichnet.

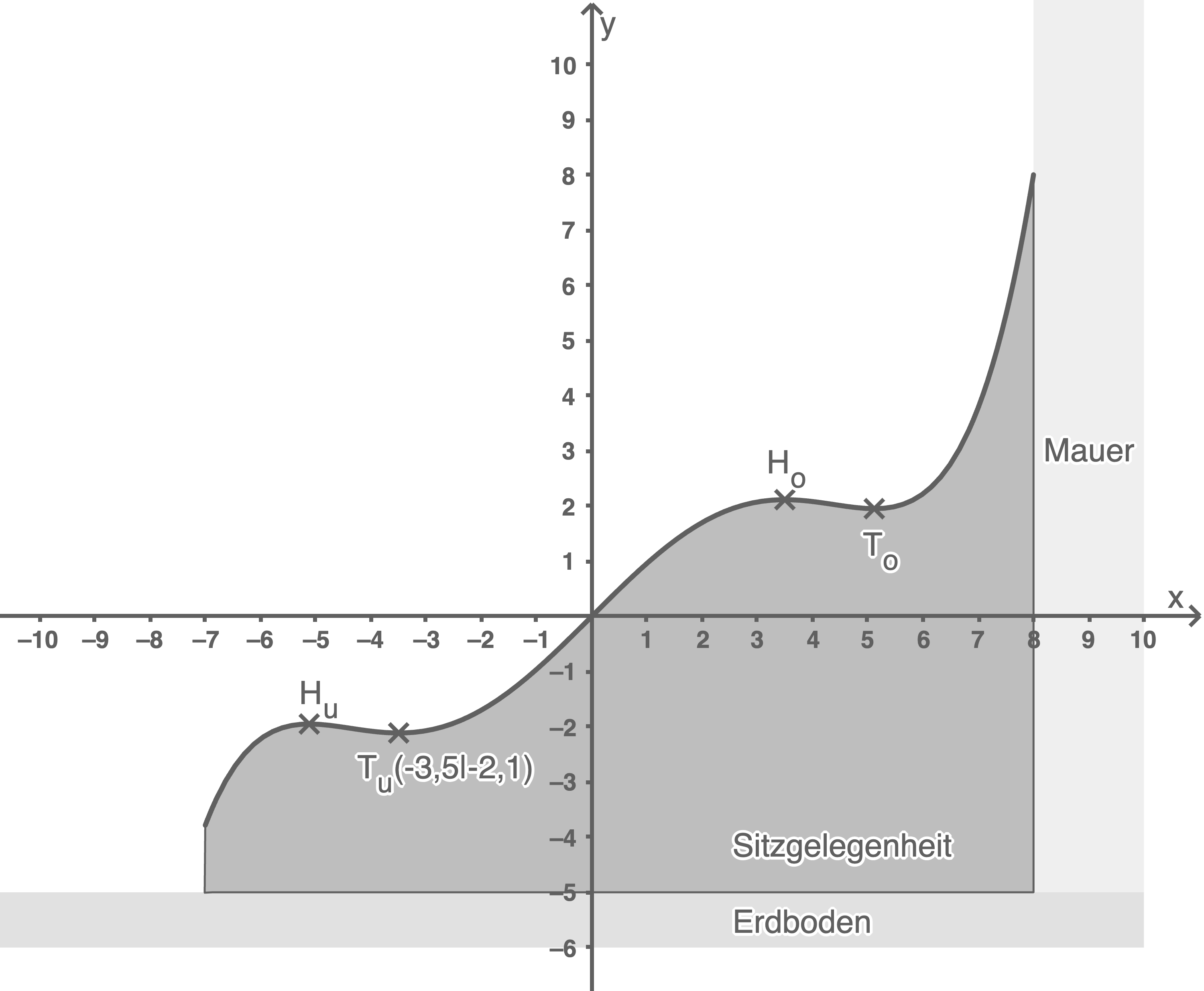
Abbildung 1

1.1

Berechne die Koordinaten von $H_u$ und $T_o.$

(4 BE)

1.2

Bestimme die Höhe der Sitzgelegenheit in Meter.

(2 BE)

1.3

Berechne die mittlere Steigung des Graphen von $q$ im Intervall $-7 \leq x \leq 8$ sowie die lokale Steigung von $q$ im Koordinatenursprung.

Die Stadtverwaltung fragt sich, ob Kinder den oberen Sitzbereich kletternd erreichen können.

Bewerte, welche der beiden Steigungen zur Klärung dieser Frage besser geeignet ist.

(6 BE)

1.4

Es werden Streckenzüge zwischen Punkten auf dem Graphen von $q$ betrachtet.

1.4.1

Beschreibe, wie man unter Verwendung von Streckenzügen zwischen Punkten auf dem Graphen von $q$ im Intervall $-7 \leq x \leq 8$ einen beliebig genauen Wert für dessen Länge in diesem Intervall erhalten kann.

(3 BE)

1.4.2

Berechne die Länge des Graphen von $q$ im Intervall $-7 \leq x \leq 8$ mit Methoden der Integralrechnung.

Formuliere eine allgemeine Aussage zur Länge des Graphen von $q$ im Vergleich zur Länge der in 1.4.1 verwendeten Streckenzüge. Begründe diese Aussage.

(4 BE)

1.4.3

Gib eine Anwendung im Sachzusammenhang an, für die die Länge des Graphen von $q$ im Intervall $-7 \leq x \leq 8$ relevant ist.

(1 BE)

Um ähnliche Sitzgelegenheiten für verschiedene Altersklassen anzubieten, sollen die Querschnitte ihrer Oberflächen durch die Funktionen der Schar $f_k$ mit der Gleichung $f_k(x)=\sin (x)+k \cdot x$ und $x, k \in \mathbb{R}$ beschrieben werden.

Nicht alle Werte von $k$ kommen dafür in Frage. Die Graphen von $f_k$ heißen $G_k.$

1.5

Zeichne $G_k$ für $k=1$ und $k=-1$ im Intervall $-5 \leq x \leq 5$ in ein gemeinsames Koordinatensystem.

(4 BE)

1.6

Begründe, dass keiner der abgebildeten Graphen ein Graph von $f_k$ ist.

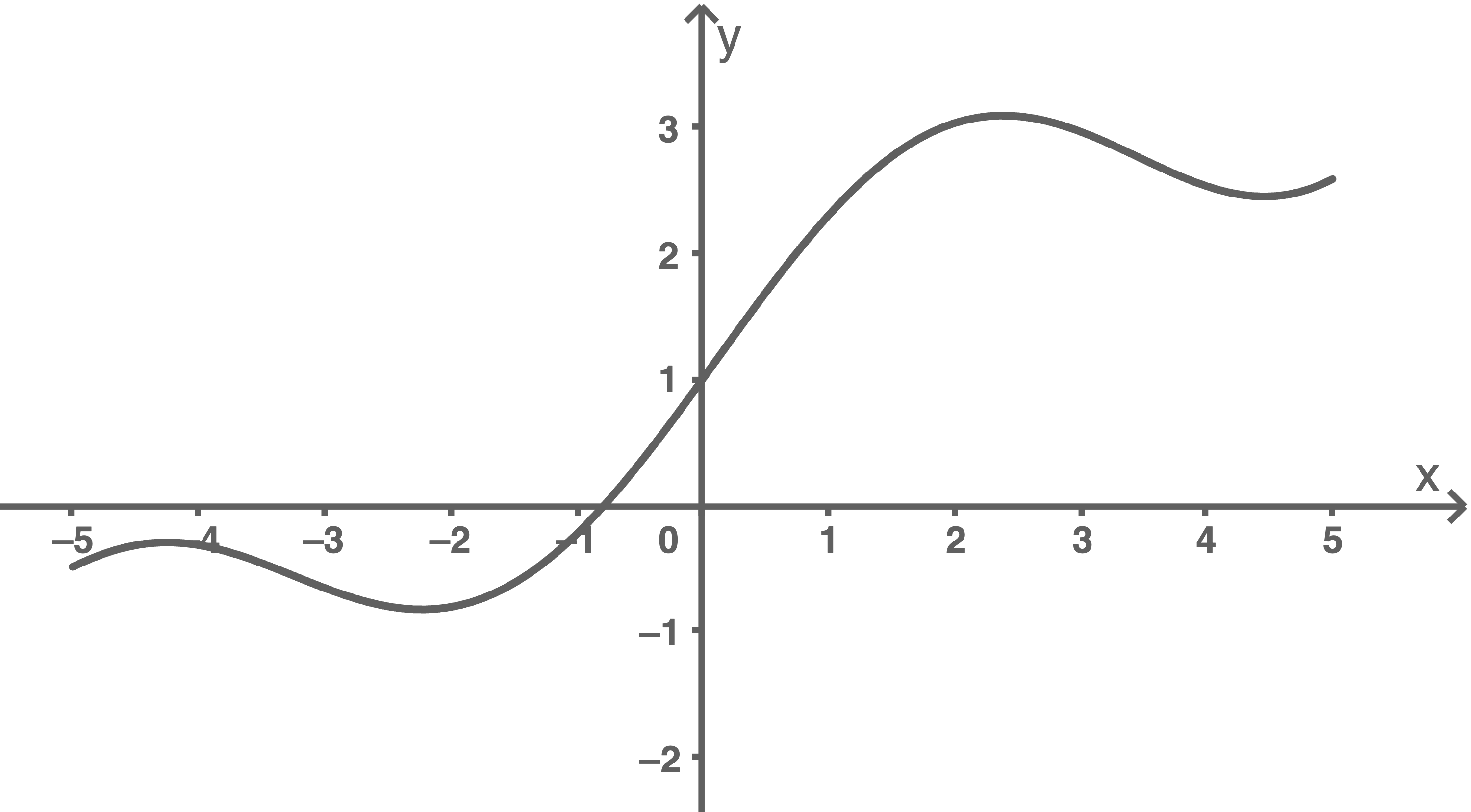
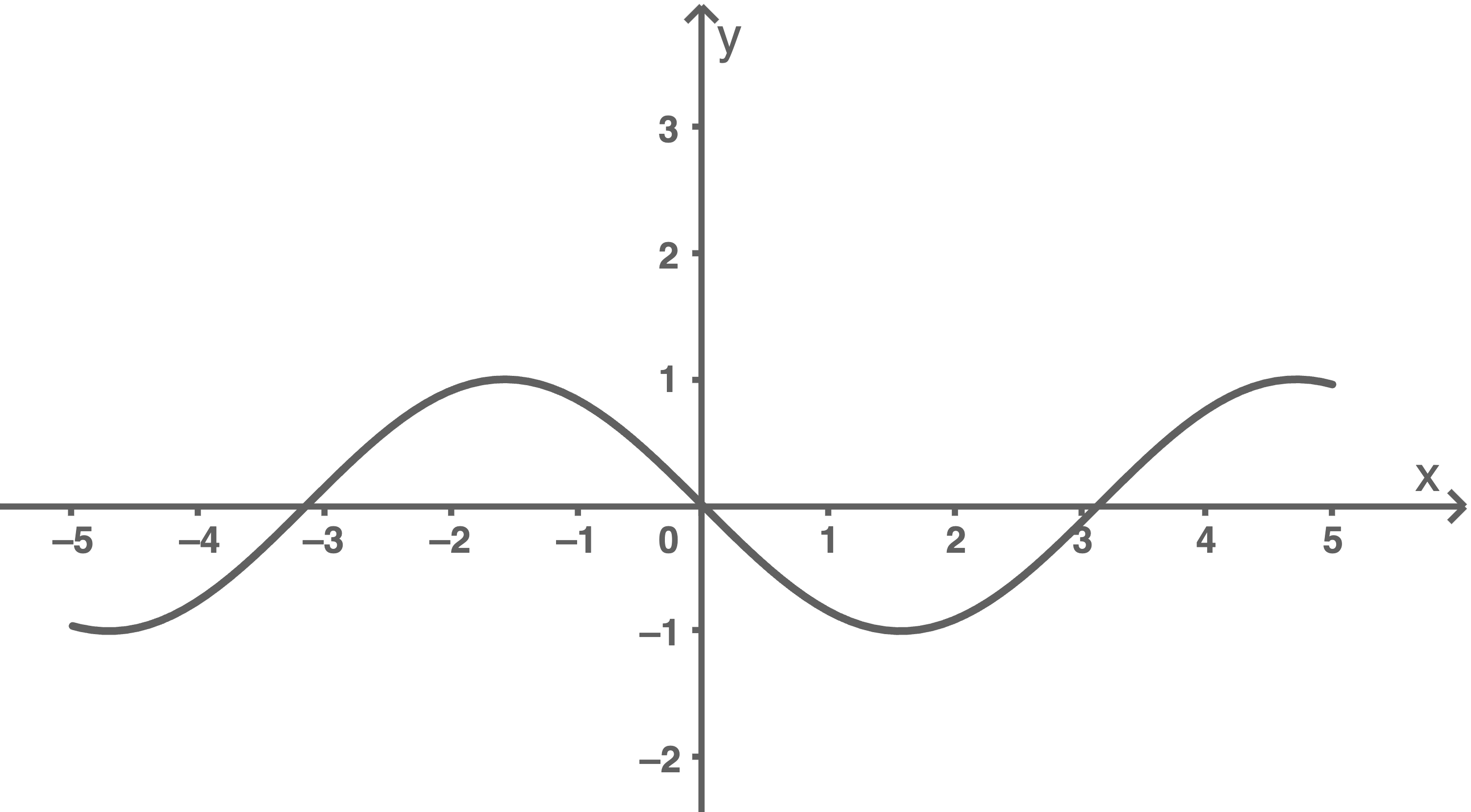
Abbildung 2

Abbildung 3

(4 BE)

1.7

Erläutere, warum es für die Eignung als Sitzgelegenheit relevant ist, dass die Graphen der Modellfunktionen Extrempunkte haben.

(2 BE)

1.8

Bestimme diejenigen Werte von $k,$ für die $G_k$ lokale Extrempunkte besitzt.

(4 BE)

1.9

Es soll ein Wert von $k$ ermittelt werden, für den $G_k$ die $x$ -Achse außerhalb des Koordinatenursprungs berührt.

Ein Lösungsweg beginnt mit den Schritten $(1)$ und $(2):$

$(1) \quad \sin (x)+k \cdot x=0, \quad \cos (x)+k=0$

$(2) \quad \Rightarrow k=-\cos (x)$ $\quad \Rightarrow \quad \sin (x)-\cos (x) \cdot x=0$ $\quad \Rightarrow \quad x=\dfrac{\sin (x)}{\cos (x)}$

Erläutere diese Schritte und bestimme einen möglichen Wert von $k.$

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

1. Schritt: Ableitung bestimmen

$\(q$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} q$

Mit dem solve-Befehl des CAS ergeben sich die möglichen Extremstellen zu:

$x_1 \approx-5,12$

$x_2 \approx-3,50$

$x_3\approx 3,50$

$x_4 \approx 5,12$

Mit Hilfe der Abbildung kann für $H_u$ bzw. $T_o$ direkt $x=-5,12$ bzw. $x=5,12$ gefolgert werden.

Da aus der Abbildung hervorgeht, dass die Extremstellen existieren und jeweils Hoch- bzw. Tiefpunkt sind, kann auf das Überprüfen der hinreichenden Bedingung verzichtet werden.

3. Schritt: $\boldsymbol{y}$ -Koordinaten berechnen

$q(-5,12) \approx -1,95$

Rechenweg anzeigen

$q(5,12) \approx 1,95$

Rechenweg anzeigen

Die gesuchten Koordinaten ergeben sich somit zu $H_u(-5,12 \mid-1,95)$ und $T_o(5,12 \mid 1,95).$

1.2

Aus der Abbildung kann abgelesen werden, dass die maximale Höhe der Sitzgelegenheit an der Randstelle $x=8$ angenommen wird.

Es gilt:

$\begin{array}[t]{rll} q(8)&=&\dfrac{1}{1600} \cdot 8^5-\dfrac{1}{25} \cdot 8^3+8 &\\[5pt] &=& 8 \end{array}$

Da die untere Begrenzung entlang der Geraden $y=-5$ verläuft, gilt für die Gesamthöhe an der Stelle $x=8$ also:

$8+5=13 \;[\text{LE}]$

Da eine Längeneinheit $1\; \mathrm{dm}$ entspricht, beträgt die Höhe der Sitzgelegenheit somit 1,3 Meter.

1.3

Mittlere Steigung berechnen

Mit dem CAS ergibt sich:

$\dfrac{q(8)-q(-7)}{8-(-7)}\approx 0,79$

Lokale Steigung bestimmen

Es gilt:

$q^{\prime}(0)=1$

Bewertung

Zur Klärung der Frage ist der Wert des steilsten Anstiegs und somit der Wert der lokalen Steigung im Koordinatenursprung relevanter. Dieser Wert stellt den tatsächlich zu überwindenden maximalen Anstieg beim Klettern dar.

Die mittlere Steigung hingegen ist lediglich ein Mittelwert, der keinerlei Auskunft darüber gibt, wie steil die Sitzgelegenheit an bestimmten Stellen tatsächlich ist.

1.4.1

Das Intervall von $x_0=-7$ bis $x_n=8$ mit $n \in \mathbb{N}$ kann mittels $x_1, x_2, \ldots, x_{n-1}$ in $n$ gleich große Teile unterteilt werden, wobei die Punkte des Graphen von $q$ mit den $x$ -Koordinaten $x_1, x_2, \ldots, x_{n}$ fortlaufend durch Strecken verbunden werden.

Die Summe der Längen dieser Strecken stimmt mit der Länge des Graphen von $q$ beliebig genau überein, wenn die Werte von $n$ hinreichend groß sind.

1.4.2

Länge berechnen

Mit der Formel für die Bogenlänge $b$ einer Funktion $q$ gilt:

$\(\begin{array}[t]{rll} b&=& \displaystyle\int_{-7}^{8} \sqrt{1+(q$

Aussage formulieren

Die Länge des Graphen von $q$ im Intervall $-7 \leq x \leq 8$ ist stets größer als die Länge eines der betrachteten Streckenzüge.

Begründung

Jede Strecke des Streckenzugs ist eine direkte Verbindung zweier Punkte des Graphen und somit kürzer als das Stück des Graphen von $q$ zwischen ihren beiden Endpunkten.

1.4.3

Die Länge des Graphen von $q$ im Intervall ist beispielsweise relevant für die Ermittlung der Flächengröße der Sitzfläche.

1.5

Mit dem CAS können die beiden Graphen dargestellt werden.

Einzeichnen in ein gemeinsames Koordinatensystem liefert:

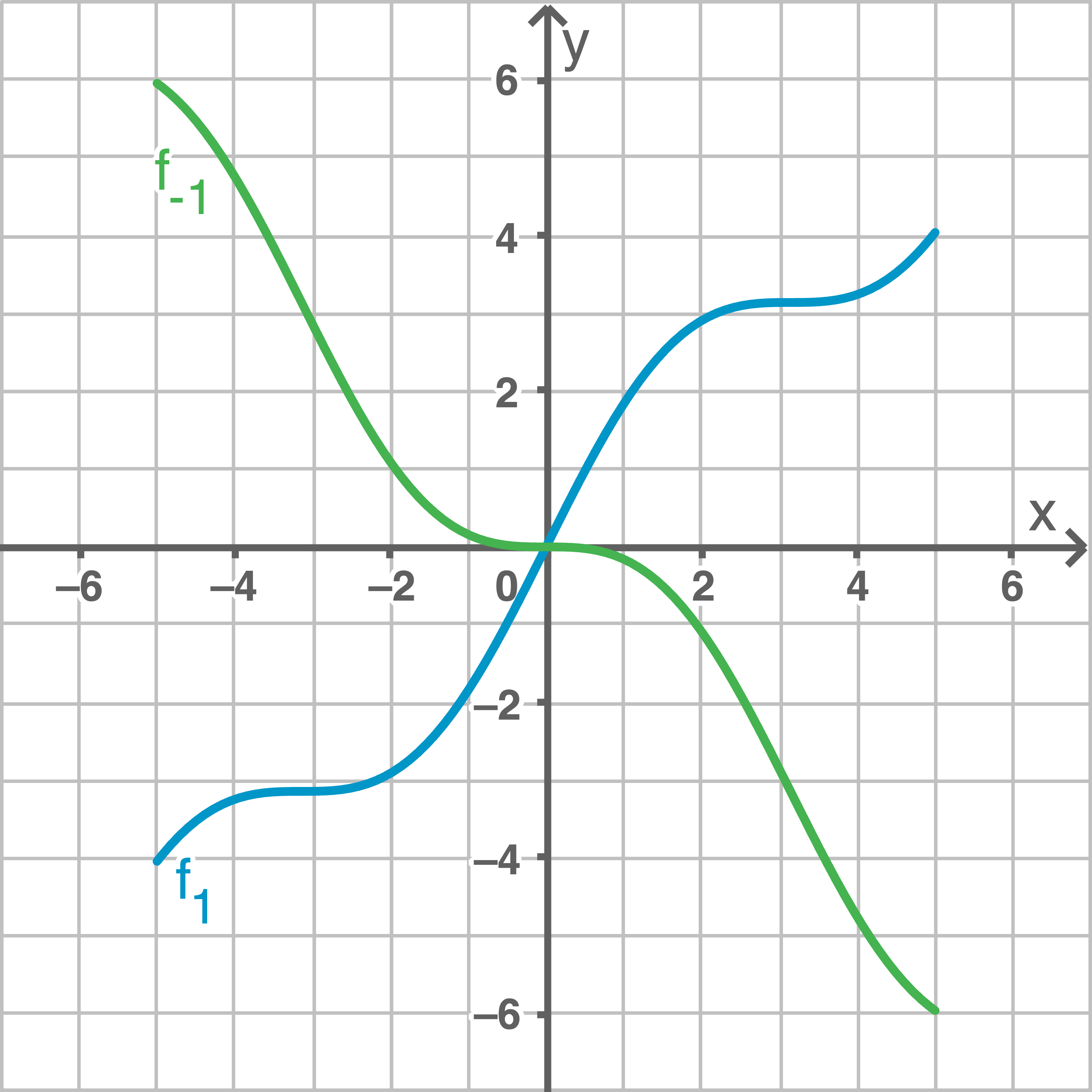
Graph Funnktionenschar MV Mathe Abi Sitzgelegenheit

1.6

Der Graph in Abbildung 2 verläuft nicht durch den Koordinatenursprung, es gilt jedoch $f_k(0)=0$ für jeden Wert von $k.$

Abbildung 3 stellt den Graphen von $f(x)=-\sin (x)$ dar. Dieser ist kein Graph der Schar $f_k,$ da für keinen Wert $k$ die Gleichung $-\sin (x)=\sin (x)+k \cdot x$ erfüllt ist.

1.7

Durch das Vorhandensein von Extrempunkten ergeben sich Sitzmulden, die für Stabilität beim Sitzen sorgen.

Ohne diese wäre die Profillinie der Sitzgelegenheit streng monoton fallend bzw. steigend und man würde beim Sitzen zwangsläufig nach unten rutschen.

1.8

1. Schritt: Ableitungen bestimmen

$\(\begin{array}[t]{rll} f_k$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_k$

Diese Gleichung besitzt nur Lösungen für $-1 \leq k \leq 1.$

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

Es gilt:

$\(\begin{array}[t]{rll} f$

Für $k=1$ bzw. $k=-1$ existieren an den relevanten Stellen also Wendepunkte mit waagerechter Tangente und somit Sattelpunkte.

Für $-1\lt k\lt 1$ gilt $\(f$

$G_k$ besitzt folglich nur für $-1\lt k \lt 1$ lokale Extrempunkte.

1.9

Schritte erläutern

$(1)$ Ein Berührpunkt mit der $x$ -Achse liegt genau dann vor, wenn der sowohl der Funktionswert als auch die erste Ableitung an einer Stelle $x$ null sind. Die zweite Gleichung stellt hierbei sicher, dass die $x$ -Achse nicht geschnitten, sondern lediglich berührt wird.

$(2)$ Die zweite Gleichung aus Schritt $(1)$ wird nach $k$ umgestellt und in die erste Gleichung aus Schritt $(1)$ eingesetzt. Die dabei entstehende Gleichung wird anschließend durch Äquivalenzumformung nach $x$ umgestellt.

Wert bestimmen

Der CAS liefert für $x=\dfrac{\sin (x)}{\cos (x)}$ beispielsweise den Wert $x\approx 4,49.$

Einsetzen in die erste Gleichung von Schritt $(2)$ ergibt folgenden Wert von $k:$

$k=-\cos (4,49) \approx 0,22$

Für weitere Lösungen $x$ mit $x \neq 0$ ergeben sich Werte $k \in\{-0,13 ;-0,07 ; 0,06 ; 0,09\}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?