2 Analytische Geometrie

Die Abbildung 1 zeigt das Viereck $A B C D$ mit $A(0\mid 3 \mid 0), B(0 \mid 9 \mid 0), C(2 \mid 8 \mid 4)$ und $D(2 \mid 4 \mid 4)$ . Gegeben sind außerdem die Punkte $S_t(0 \mid 6 \mid t)$ mit $t \in \mathbb{R}_0^{+}.$

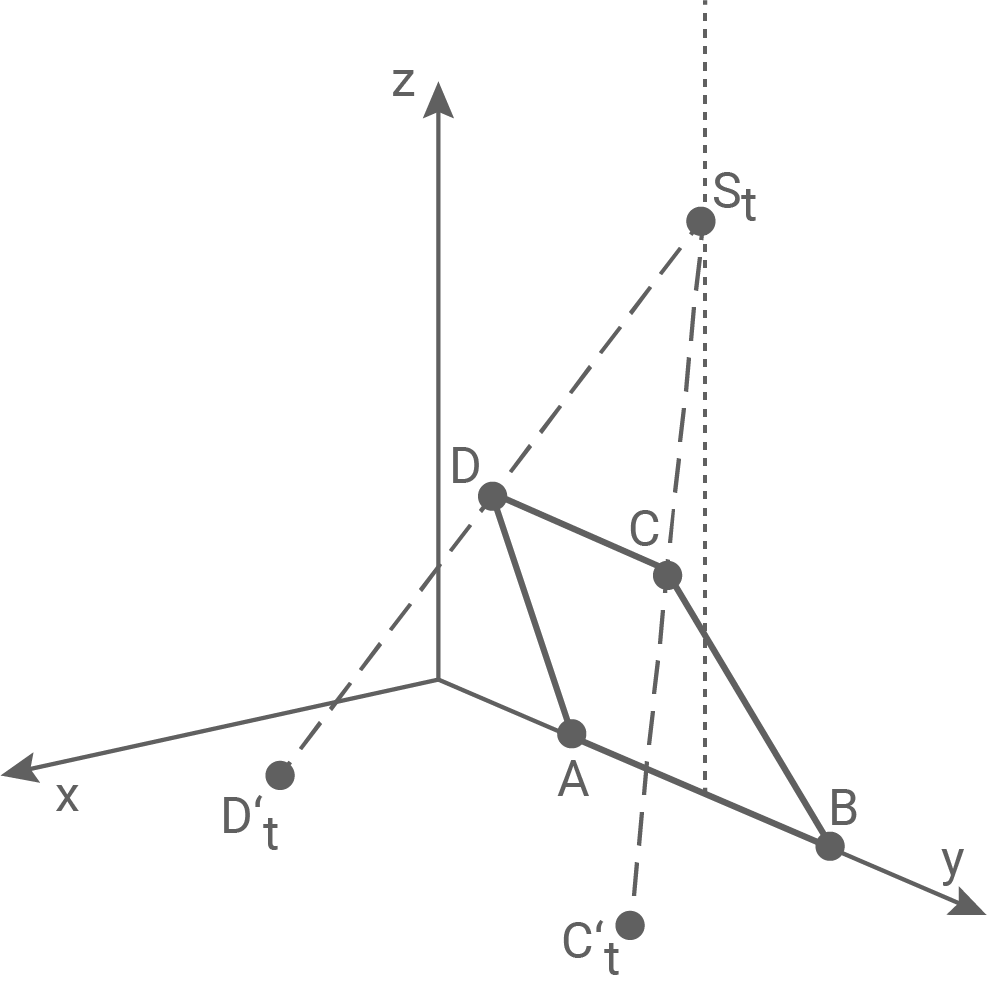
Trapez im dreidimensionalen Koordinatensystem Abi 2023

Abbildung 1

2.1

Weise nach, dass das Viereck $A B C D$ ein Trapez ist, in dem zwei gegenüberliegende Seiten gleich lang sind, und dass dieses Trapez kein Rechteck ist.

(4 BE)

2.2

Berechne den Flächeninhalt des Vierecks $A B C D.$

(3 BE)

2.3

Bestimme eine Gleichung der Ebene $E$ , in der das Viereck $A B C D$ liegt, in Koordinatenform.

(zur Kontrolle: $2 x-z=0)$

(3 BE)

2.4

Die Ebene $E$ schneidet die $xz$ -Ebene in einer Gerade.
Gib die Koordinaten zweier Punkte an, die auf dieser Gerade und symmetrisch bezüglich des Koordinatenursprungs liegen.

(2 BE)

2.5

Vom Punkt $S_t$ aus wird das Lot auf die Ebene $E$ gefällt. Ermittle diejenigen Werte von $t,$ für die der Lotfußpunkt im Inneren des Vierecks $A B C D$ liegt.

(5 BE)

Im Folgenden gilt $t>4$ .

Die Gerade durch die Punkte $S_t$ und $C$ schneidet die $xy$ -Ebene im Punkt $C_t^{\prime}$ , die Gerade durch die Punkte $S_t$ und $D$ schneidet diese Ebene im Punkt $D_t^{\prime}$ (vgl. Abbildung 1).

2.6

Die beiden folgenden Gleichungen I und II liefern gemeinsam einen bestimmten Wert von $t$ .

I $\quad \overrightarrow{\mathrm{OS}_{\mathrm{t}}}+r \cdot \overrightarrow{\mathrm{S}_{\mathrm{t}} \mathrm{C}}=\overrightarrow{\mathrm{OC}_{\mathrm{t}}^{\prime}}$ mit $C_{\mathrm{t}}^{\prime}(x\mid y\mid 0)$

II $\quad\overrightarrow{\mathrm{BA}} \circ\overrightarrow{\mathrm{BC}_{\mathrm{t}}^{\prime}}=0$

Gib für diesen Wert von $t$ die Art des Vierecks $A B C_t^{\prime} D_t^{\prime}$ an und begründe deine Angabe.

(5 BE)

2.7

Das Volumen der Pyramide $A B C_t^{\prime} D_t^{\prime} S_t$ wird in Abhängigkeit von $t$ durch einen der drei abgebildeten Graphen $G_1, G_2$ und $G_3$ dargestellt (vgl. Abbildung 2).
Gib diesen Graphen an und begründe deine Angabe.

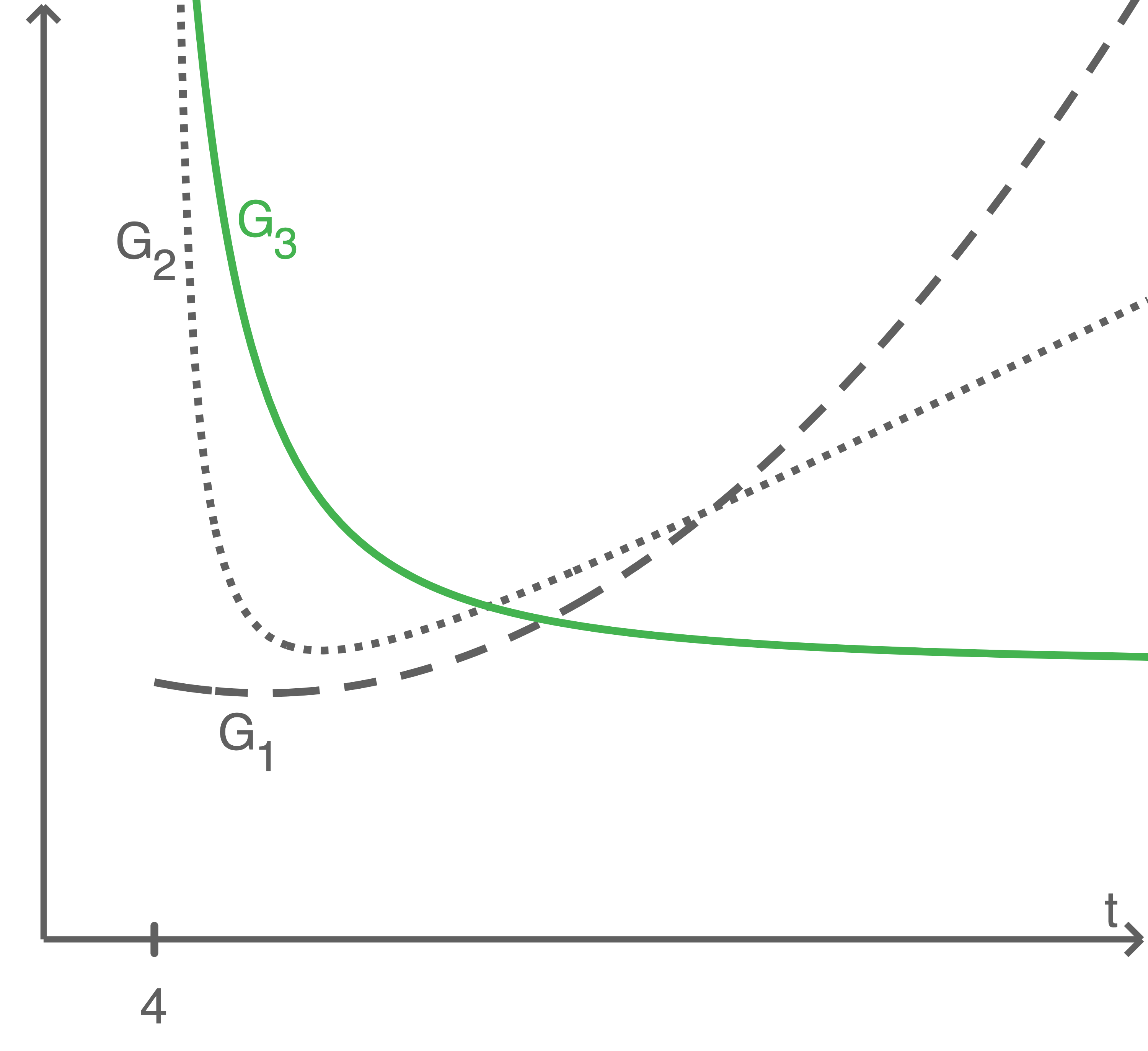
Abbildung 2

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Trapezform nachweisen

In einem Trapez müssen zwei gegenüberliegende Seiten parallel sein. In der Abbildung lässt sich erkennen, dass es sich vermutlich um $\overline{AB}$ und $\overline{CD}$ handelt.

$\overrightarrow{AB} = \pmatrix{0\\ 6\\ 0}$

$\overrightarrow{CD} = \pmatrix{0\\ -4\\ 0}$

Es gilt $\overrightarrow{AB} = -\frac{3}{2}\cdot \overrightarrow{CD}.$

$\overrightarrow{AB}$ und $\overrightarrow{CD}$ sind also linear abhängig. Somit sind $\overline{AB}$ und $\overline{CD}$ parallel.

Es handelt sich also um ein Trapez.

Gleiche Länge zweier gegenüberliegender Seiten nachweisen

Rechenweg anzeigen

$\overline{BC} = \sqrt{21}$

Rechenweg anzeigen

$\overline{AD} = \sqrt{21}$

Die gegenüberliegenden Seiten $\overline{AC}$ und $\overline{AD}$ sind also gleich lang.

Nachweisen, dass es sich nicht um ein Rechteck handelt

$\overrightarrow{AB} \circ \overrightarrow{BC}=\left(\begin{array}{l}0 \\ 6 \\ 0\end{array}\right) \circ\left(\begin{array}{c}2 \\ -1 \\ 4\end{array}\right)= -6 \neq 0$

Da das Skalarprodukt der Vektoren $\overrightarrow{A B}$ und $\overrightarrow{BC}$ nicht null ist, befindet sich im Punkt $B$ kein rechter Winkel. Es kann sich also nicht um ein Rechteck handeln.

2.2

1. Schritt: Höhe des Trapezes berechnen

Da $A$ und $B$ auf der $y$ -Achse liegen, entspricht die Höhe des Trapezes dem Abstand von $D$ zur $y$ -Achse.

Aus den Koordinaten von $D$ lassen sich direkt die Koordinten des Fußpunktes des Lots von $D$ auf die $y$ -Achse herleiten: $L(0\mid 4\mid 0).$

Daraus folgt die Höhe des Trapezes:

Rechenweg anzeigen

$h=\sqrt{20}\; \text{[LE]}$

2. Schritt: Längen der gegenüberliegenden Seiten berechnen

$\overline{AB} = \left|\overrightarrow{AB} \right| = \left|\pmatrix{0\\6\\0} \right| = 6\; \text{[LE]}$

$\overline{CD} = \left|\overrightarrow{CD} \right| = \left|\pmatrix{0\\-4\\0} \right| = 4\; \text{[LE]}$

3. Schritt: Flächeninhalt berechnen

Rechenweg anzeigen

$A =10 \sqrt{5}\; \text{[FE]}$

2.3

Mit dem Kreuzprodukt und dem CAS kann ein Normalenvektor von $E$ bestimmt werden:

Rechenweg anzeigen

$\overrightarrow{n}= 12 \cdot\left(\begin{array}{c}2 \\ 0 \\ -1\end{array}\right)$

Einsetzen der Koordinaten von $A$ und $\overrightarrow{n}$ in die allgemeine Ebenengleichung in Koordinatenform:

$d = 2 \cdot 0+0 \cdot 3-1 \cdot 0=0$

Die Koordinatengleichung der Ebene lautet demnach $E: 2x-z=0.$

2.4

Da die Kante $\overline{A B}$ des Trapezes auf der $y$ -Achse liegt, beinhaltet $E$ die $y$ -Achse.
Die Schnittgerade von $E$ mit der $\mathrm{xz}$ -Ebene verläuft somit durch den Koordinatenursprung.
Für die $xz$ -Ebene gilt $y=0.$ Einsetzen in die Ebenengleichung von $E:$

$2x-z = 0$

Wird $t$ als Geradenparameter verwendet, kann beispielsweise $x=t$ festgelegt werden. Aus $2t -z = 0$ folgt dann $z =2t.$

Für die Punkte auf der Schnittgeraden mit dem Geradenparameter $t$ gilt also $x= t,$ $y = 0$ und $z=2t.$

$s: \, \overrightarrow{x} = t\cdot \pmatrix{1\\ 0\\ 2}=\pmatrix{0\\0\\0} + t\cdot \pmatrix{1\\ 0\\ 2}$

Da der Stützpunkt der Schnittgeraden der Koordinatenursprung ist, ergibt sich eines der gesuchten Punktpaare beispielsweise für $t=1$ und $t=-1:$

$\overrightarrow{OP}_1 = \pmatrix{0\\0\\0} + 1\cdot \pmatrix{1\\ 0\\ 2} = \pmatrix{1\\0\\2}$

$\overrightarrow{OP}_2 = \pmatrix{0\\0\\0} + -1\cdot \pmatrix{1\\ 0\\ 2} = \pmatrix{-1\\0\\-2}$

$P_1(1\mid 0 \mid 2 )$ und $P_2(-1\mid 0\mid -2)$ liegen auf der Schnittgeraden und symmetrisch bezüglich des Koordinatenursprungs.

2.5

1. Schritt: Gleichung der Lotgerade bestimmen

Da die Lotgerade senkrecht zu $E$ verläuft, kann ein Normalenvektor von $E$ als Richtungsvektor verwendet werden:

$\overrightarrow{r}= \pmatrix{2\\0\\-1}$

Der Punkt $S_t$ wird also Stützpunkt verwendet:

$l:\, \overrightarrow{x} = \pmatrix{0\\6\\t} + s\cdot \pmatrix{2\\0\\-1}$

2. Schritt: Koordinaten des Lotfußpunkts bestimmen

Der Lotfußpunkt ist der Schnittpunkt der Lotgerade mit der Ebene $E.$ Für die Punkte auf der Lotgeraden gilt $x= 2s,$ $y= 6$ und $z= t-s.$ Einsetzen in die Ebenengleichung:

$\begin{array}[t]{rll} E:\, 2x -z &=& 0 \\[5pt] 2\cdot (2s) -(t-s) &=& 0 \\[5pt] 5s -t &=& 0 &\quad \scriptsize \mid\;+t \\[5pt] 5s &=& t &\quad \scriptsize \mid\; :5 \\[5pt] s &=& 0,2t \end{array}$

Einsetzen in die Geradengleichung:

$\overrightarrow{OL} = \pmatrix{0\\6\\t} + 0,2t\cdot \pmatrix{2\\0\\-1}=\pmatrix{0,4t \\ 6 \\ 0,8t}$

$L(0,4t \mid 6\mid 0,8t)$

3. Schritt: Werte für $\boldsymbol{t}$ ermitteln

Damit $L$ im Viereck $ABCD$ liegt, muss unter anderem $0\lt x \lt 2$ gelten:

$\begin{array}[t]{rll} 0 &\lt & x &\lt& 2 \\[5pt] 0 &\lt & 0,4t &\lt& 2 &\quad \scriptsize \mid\;:0,4 \\[5pt] 0 &\lt & t &\lt& 5 \\[5pt] \end{array}$

Die $y$ -Koordinate ist konstant. Für die $z$ -Koordinate muss gelten:

$\begin{array}[t]{rll} 0 &\lt & z &\lt& 4 \\[5pt] 0 &\lt & 0,8t &\lt& 4 &\quad \scriptsize \mid\;:0,8 \\[5pt] 0 &\lt & t &\lt& 5 \\[5pt] \end{array}$

Für $0\lt t\lt 5$ liegt der Lotfußpunkt innerhalb des Vierecks $ABCD.$

2.6

Gleichung I liefert den Schnittpunkt $C_t$ der Geraden durch $S_t$ und $C$ mit der $xy$ -Ebene.

Gleichung II liefert den Wert von $t,$ sodass das Viereck $A B C_t D_t$ im Punkt $B$ einen rechten Winkel hat.

$S_t$ liegt in der Ebene $y=6,$ die Eckpunkte des Trapezes liegen symmetrisch bezüglich dieser Ebene. Folglich ist das Viereck $A B C_t D_t$ auch im Punkt $A$ rechtwinklig und die Seiten $\overline{A B}$ und $\overline{C_t D_t}$ verlaufen parallel. Somit ist das Viereck $ABC_{t} D_{t}$ ein Rechteck.

2.7

Für den Wert $t \rightarrow 4$ verlaufen die Kanten $\overline{S_t C_t}$ und $\overline{S_t D_t}$ immer flacher zur $xy$ -Ebene. Folglich wird der Flächeninhalt des Vierecks $A B C_t D_t$ beliebig groß. Somit wird auch das Volumen für $t \rightarrow 4$ beliebig groß. Deshalb kann Graph $G_1$ ausgeschlossen werden.

Für $t \rightarrow \infty$ wird die Höhe beliebig groß. Der Inhalt der Grundfläche $A B C_t D_t$ strebt gegen einen festen Wert, da die Punkte $C_t$ und $D_t$ gegen die Punkte $(2\mid 8\mid 0)$ und $(2\mid 4\mid 0)$ gehen (senkrecht unter den Punkten $A$ und $B$ in der $x y$ -Ebene). Folglich wird das Volumen beliebig groß. Somit kann Graph $G_3$ ausgeschlossen werden.

Es ist Graph $G_2$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?