Analytische Geometrie

Die Abbildung 1 zeigt das sogenannte Saarpolygon, ein im Inneren begehbares Denkmal zur Erinnerung an den stillgelegten Kohlebergbau im Saarland. Das Saarpolygon kann in einem Koordinatensystem modellhaft durch den Streckenzug dargestellt werden, der aus den drei Strecken $\overline{AB,}$ $\overline{BC}$ und $\overline{CD}$ mit $A(11\mid 11\mid 0),$ $B(-11\mid 11\mid 28),$ $C(11\mid -11\mid 28)$ und $D(-11\mid -11\mid 0)$ besteht (vgl. Abbildung 2).

$A,$ $B,$ $C$ und $D$ sind Eckpunkte eines Quaders. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.

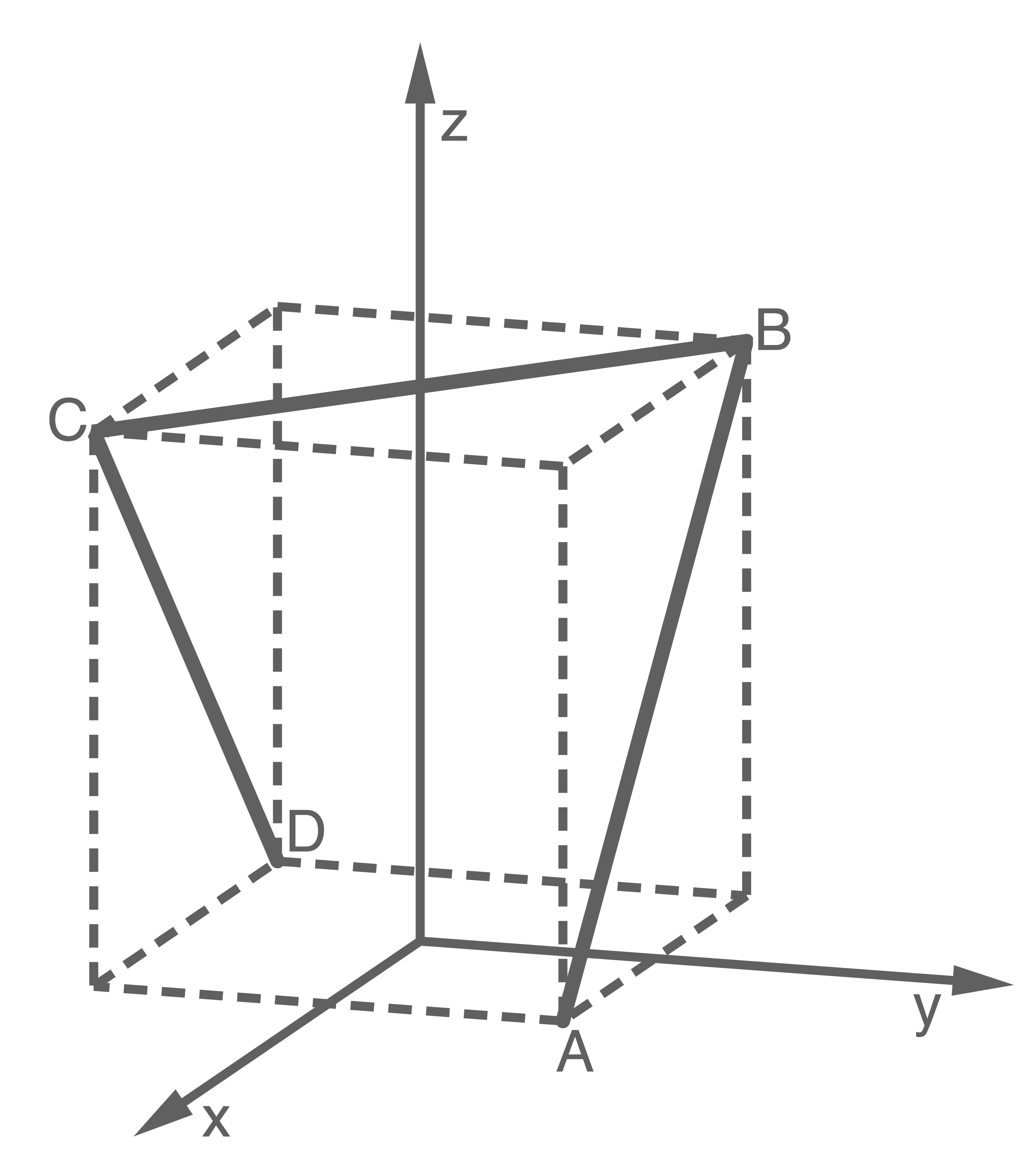
Abbildung 1

Mecklenburg-Vorpommern Abi 2022 Saarpolygon

Abbildung 2

2.1

Begründe, dass die Punkte $B$ und $C$ symmetrisch bezüglich der $z$ -Achse liegen.

(2 BE)

2.2

Berechne die Länge des Streckenzugs in der Wirklichkeit.

(3 BE)

2.3

Die Ebene $E$ enthält die Punkte $A,$ $B$ und $C,$ die Ebene $F$ die Punkte $B,$ $C$ und $D.$

2.3.1

Bestimme eine Gleichung von $E$ in Koordinatenform.

zur Kontrolle: $14x+14y+11z=308$

(3 BE)

2.3.2

Berechne die Größe $\varphi$ des Winkels, unter dem $E$ die $xy$ -Ebene schneidet.

Gib einen Term an, mit dem aus $\varphi$ die Größe des Winkels zwischen den Ebenen $E$ und $F$ berechnet werden kann.

(5 BE)

2.3.3

Die Ebene $E$ teilt den Quader in zwei Teilkörper. Bestimme das Verhältnis der Volumina der beiden Teilkörper, ohne die Volumina zu berechnen.

(4 BE)

2.4

Das Saarpolygon wird mit verschiedenen Blickrichtungen betrachtet. Die Abbildungen 3 und 4 stellen das Saarpolygon für zwei Blickrichtungen schematisch dar.

Abbildung 3

Abbildung 4

Gib zu jeder der beiden Abbildungen 3 und 4 einen möglichen Vektor an, der die zugehörige Blickrichtung beschreibt.

Stelle das Saarpolygon schematisch für eine Betrachtung von oben dar.

(4 BE)

2.5

Der Punkt $P(0\mid 0\mid h)$ liegt innerhalb des Quaders und hat von den drei Strecken $\overline{AB},$ $\overline{BC}$ und $\overline{CD}$ den gleichen Abstand. Das folgende Gleichungssystem liefert den Wert von $h:$

I $\quad$ $\overrightarrow{OQ}=\pmatrix{11\\11\\0}+t\cdot\pmatrix{-22\\0\\28},t\in\left[0;1\right]$

II $\quad$ $\overrightarrow{PQ}\circ\overrightarrow{AB}=0$

III $\quad$ $\left|\overline{PQ}\right|=28-h$

Erläutere die Überlegungen, die diesem Vorgehen zur Bestimmung des Werts von $h$ zugrunde liegen.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Sowohl die $x$ -Koordinaten als auch die $y$ -Koordinaten von $B$ und $C$ unterscheiden sich nur in ihren Vorzeichen, die $z$ -Koordinaten stimmen überein.

Alternative: $B$ und $C$ besitzen die gleiche $z$ -Koordinate, $\overline{ BC }$ verläuft somit senkrecht zur $z$ -Achse. Der Mittelpunkt $M$ der Strecke $\overline{ BC }$ liegt auf der $z$ -Achse:

$M\left(\dfrac{-11+11}{2}\left|\dfrac{11-11}{2}\right| \dfrac{28+28}{2}\right)$ $=M(0|0| 28)$ .

2.2

$|\overrightarrow{ AB }|+|\overrightarrow{ BC }|+|\overrightarrow{ CD }|$ $=\left|\left(\begin{array}{c} -22 \\ 0 \\ 28 \end{array}\right)\right|+\left|\left(\begin{array}{c} -22 \\ -22 \\ 0 \end{array}\right)\right|+\left|\left(\begin{array}{c} -22 \\ 0 \\ -28 \end{array}\right)\right|$ $\approx 102,3$

Die Gesamtlänge beträgt rund $102,3\,\text{m.}$

2.3.1

Ein Normalvektor von $E$ ergibt sich aus:

$\vec{n}=\overrightarrow{ AB } \times \overrightarrow{ AC }$ $=\left(\begin{array}{c} -22 \\ 0 \\ 28 \end{array}\right) \times\left(\begin{array}{c} 0 \\ -22 \\ 28 \end{array}\right)$ $=\left(\begin{array}{l} 616 \\ 616 \\ 484 \end{array}\right)=44 \cdot\left(\begin{array}{c} 14 \\ 14 \\ 11 \end{array}\right)$

Einsetzen des Punktes $A$ in $a \cdot x+b \cdot y+c \cdot z=d$ , wobei $a,$ $b$ und $c$ Koordinaten von $\vec{n}$ sind, liefert:

$14 \cdot 11+14 \cdot 11+11 \cdot 0=308$

Folglich ergibt sich die Gleichung $E: 14 \cdot x+14 \cdot y+11 \cdot z=308$

Alternativ kann die Ebenengleichung in Koordinatenform auch über die Normalenform bestimmt werden: $E:(\overrightarrow{O A}-\vec{x}) \circ \vec{n}=0$ liefert mit dem CAS mit $\vec{x}=\left(\begin{array}{l}x \\ y \\ z\end{array}\right)$ die Ebenengleichung $E=14 \cdot x+14 \cdot y+11 \cdot z-308=0$

2.3.2

Neigungswinkel von $E$ zur $xy$ -Ebene:

$\varphi=\arccos \left(\dfrac{\left(\begin{array}{l}14 \\ 14 \\ 11\end{array}\right) \cdot\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)}{\left(\begin{array}{l}14 \\ 14 \\ 11\end{array}\right) \cdot\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)}\right)$ $\approx 60,9^{\circ}$

Aufgrund der gemeinsamen Kante $\overline{ BC }$ und ihrer Lage zum Quader sind die Ebenen $E$ und $F$ im gleichen Winkel zur $xy$ -Ebene geneigt. Term zur Berechnung des Winkels zwischen $E$ und $F:$ $\sphericalangle_{E F}=180^{\circ}-2 \cdot \varphi$

2.3.3

Bezeichnet man mit $S$ die Ecke des Quaders mit positiven Koordinaten, dann erzeugen die Vektoren $\overrightarrow{ SA }, \overrightarrow{ SB }$ und $\overrightarrow{ SC }$ den Quader als Spat und einen der beiden Teilkörper als dreiseitige Pyramide. Das Volumen der Pyramide entspricht $\dfrac{1}{6}$ des Volumens des Spats. Somit beträgt das Volumen des verbleibenden Teilkörpers $\dfrac{5}{6}$ des Spatvolumens.

Das Verhältnis der beiden Teilvolumina ist daher 1:5

2.4

Abb. 3 entsteht durch die Betrachtung in $y$ -Richtung: $\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right)$ bzw. $\left(\begin{array}{c}0 \\ -1 \\ 0\end{array}\right)$ .

Abb. 4 entsteht durch Betrachtung in Richtung des Vektors $\overrightarrow{B C}=\left(\begin{array}{c}1 \\ -1 \\ 0\end{array}\right)$ .

Darstellung der Draufsicht:

Mecklenburg-Vorpommern Abi 2022 Draufsicht

2.5

I liefert die Koordinaten eines Punktes $Q$ auf der Strecke $\overline{AB}$ .

II $\overline{ AB }$ steht senkrecht zu $\overline{PQ}$ .

III Der Abstand von $P$ und $Q$ muss mit dem Abstand zwischen $P$ und $M$ (aus 2.1) übereinstimmen. Da $M$ ebenfalls auf der $z$ -Achse liegt und die $z$ -Koordinate 28 besitzt, entspricht die Differenz der $z$ -Koordinaten von $M$ und $P$ dem Abstand von $P$ und $Q$ und liefert somit den Wert von $h$ .

Aufgrund der Symmetrie des Quaders hat die Strecke $\overline{C D}$ den gleichen Abstand zu $P$ , wie $P$ zu $\overline{A B}$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?