Analysis

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $s$ und $p$ mit den Gleichungen

$s(x)=-0,38\cdot \sin(0,6\cdot (x-1))+7,5$ und

$p(x)=0,008\cdot (0,24\cdot (x-15))^5$ $-0,09\cdot (x-15)+6,2.$

Der Graph von $s$ heißt $S,$ der Graph von $p$ heißt $P.$

Mecklenburg-Vorpommern Abi 2022 Funktionen s und p

1.1

Gib den Wertebereich von $s$ an.

Berechne für $S$ die Koordinaten und Art der lokalen Extrempunkte im Intervall $\left[0;4\pi\right].$

(5 BE)

1.2

Interpretiere bezogen auf $P$ die folgenden wahren Aussagen:

(1) Für $x\approx 7,7$ sowie $x\approx 22,3$ gilt: $\(p$ und $\(p$

(2) Es gilt: $\(p$ und $\(p$

(4 BE)

1.3

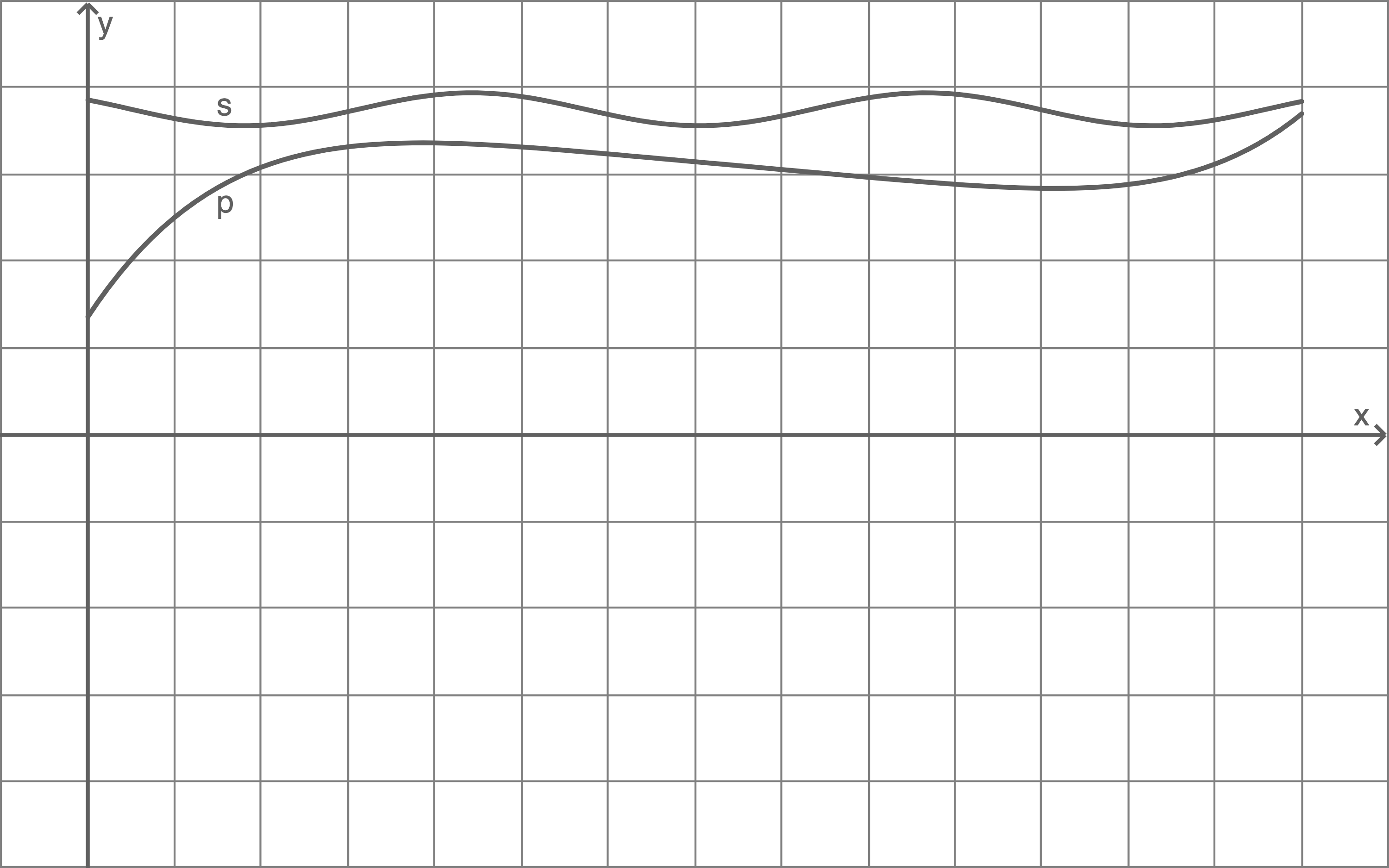
Im Schaubild oben in der Einführung sind im Koordinatensystem Ausschnitte der Graphen $S$ und $P$ dargestellt: Ergänze dafür die Skalierungen der $x$ -Achse und der $y$ -Achse.

(2 BE)

1.4

Abbildung 1 zeigt den Längsschnitt einer rotationssymmetrischen Designer-Vase, die vollständig aus Kristallglas mit einer Dichte von $2,45\,\dfrac{\text{g}}{\text{cm}^3}$ besteht. Der Vasenkörper wird durch Rotation einer Fläche $F$ um die $x$ -Achse modelliert. $F$ entspricht dabei der Fläche, die eingeschlossen wird von $S$ im Intervall $\left[0;28\right],$ $P$ im Intervall $\left[2;28\right],$ der $x$ -Achse im Intervall $\left[0;2\right]$ und den senkrecht zur $x$ -Achse verlaufenden Verbindungslinien. Der Teil von $F$ im Intervall $\left[0;2\right]$ erzeugt bei der Rotation den $2\,\text{cm}$ hohen Boden der Vase. Eine Längeneinheit entspricht einem Zentimeter.

Mecklenburg-Vorpommern Abi 2022 Designervase

Abbildung 1

1.4.1

Schraffiere in der Darstellung oben in der Einführung im Koordinatensystem die Fläche $F.$

(1 BE)

1.4.2

Berechne den Durchmesser des Bodens im Inneren der Vase sowie den Durchmesser der Standfläche der Vase.

(4 BE)

Die Glasdicke $g$ der Vase wird oberhalb ihres Bodens zwischen Innen- und Außenwand parallel zum Boden gemessen.

1.4.3

Berechne für die Vase die größte Glasdicke $g.$

(6 BE)

1.4.4

Eine der Abbildungen (A), (B), (C) aus Abbildung 2 stellt für diese Vase die Abhängigkeit der Glasdicke $g$ von der Höhe $x,$ gemessen über dem Vasenboden, dar.

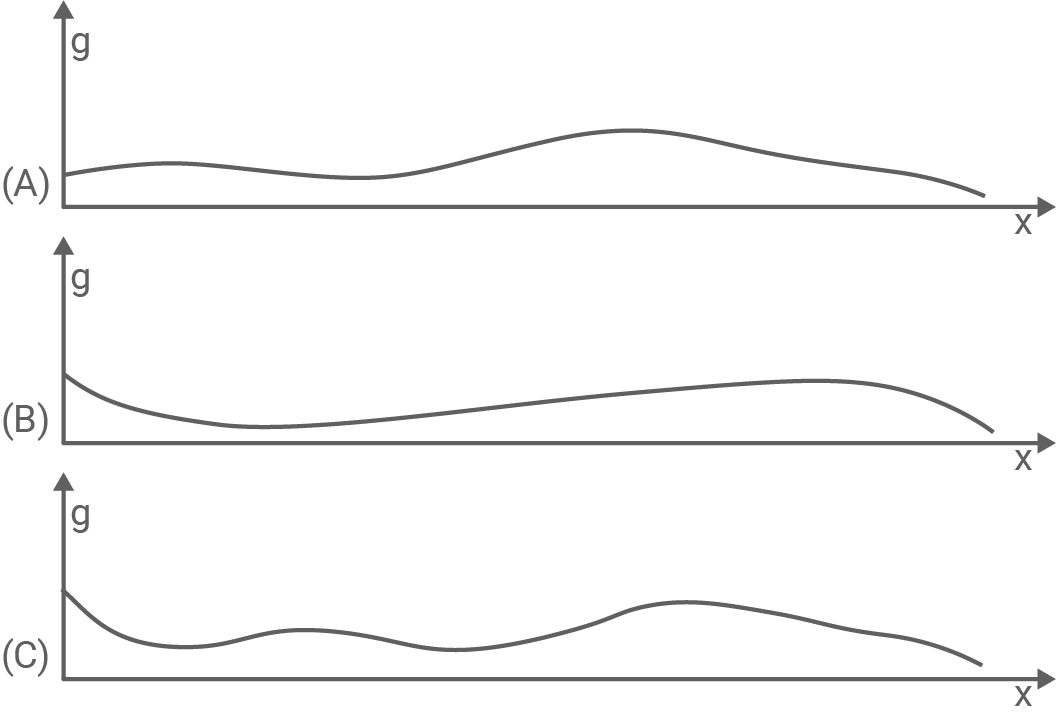Mecklenburg-Vorpommern Abi 2022 Designervase Abbildungen

Abbildung 2

Entscheide, welche der Abbildungen dies leistet. Begründe deine Entscheidung anhand von Eigenschaften der Graphen.

(4 BE)

1.4.5

Berechne die Masse der Vase in Kilogramm.

(6 BE)

1.4.6

Der gerade verlaufende Metallstiel einer Keramikblume ist an der Innenwand der Vase angelehnt und endet am gegenüberliegenden Bereich der Innenwand. Dabei kann das untere Stielende auch oberhalb des Bodens die Vasenwand berühren. (siehe Abbildung 1)

Da der Blumenkopf recht schwer ist, steht die Blume nur dann sicher in der Vase, wenn der Neigungswinkel des Stiels zur Bodenfläche mindestens 55° beträgt.

Untersuche, in welcher Höhe über dem Boden sich das untere Stielende der Keramikblume höchstens befinden darf, damit diese noch sicher in der Vase steht.

(8 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Wertebereich: $\{s(x) \in \mathbb R \mid 7,12 \leq s ( x ) \leq 7,88\}$

1. Schritt: Ableitungen bestimmen

$\(s$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(s$ mit $0 \leq x \leq 4 \pi.$

Rechenweg anzeigen

$x= \dfrac{5}{6}\cdot \pi+1$

$x_1=\dfrac{5 \pi}{6}+1 \approx 3,62,$ $x_2=\dfrac{5 \pi}{2}+1 \approx 8,85$

2. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$s^{\prime \prime}\left( x _{1}\right)\gt 0$

$s^{\prime \prime}\left( x _{2}\right)\lt 0$

$s\left( x _{1}\right) \approx 7,12$

$s\left( x _{2}\right) \approx 7,88$

Daraus folgen die Koordinaten des Tiefpunktes und des Hochpunktes mit $T(3,62 \mid 7,12),$ $H (8,85 \mid 7,88).$

1.2

Aussage (1): Notwendiges und hinreichendes Kriterium für einen Extrempunkt sind erfüllt. Somit hat der Graph von $p$ näherungsweise bei $x \approx 7,7$ und $x \approx 22,3$ zwei Extremstellen.

Aussage (2): Da $p$ eine ganzrationale Funktion ist, hat die zweite Ableitung in $[14,9\lt x\lt 15,1]$ eine Nullstelle. Der Graph von $p$ hat im Intervall einen Krümmungswechsel/Wendepunkt (Wechsel von rechtsgekrümmt in linksgekrümmt).

1.3

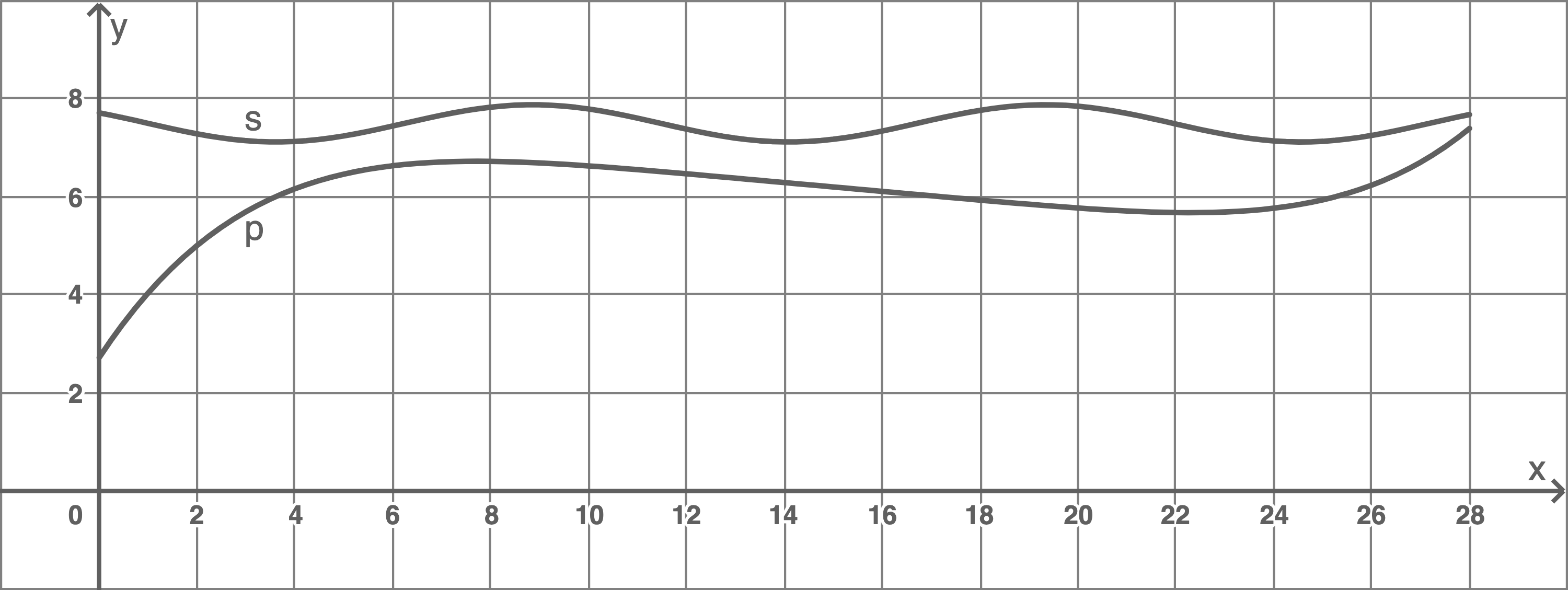
1.4.1

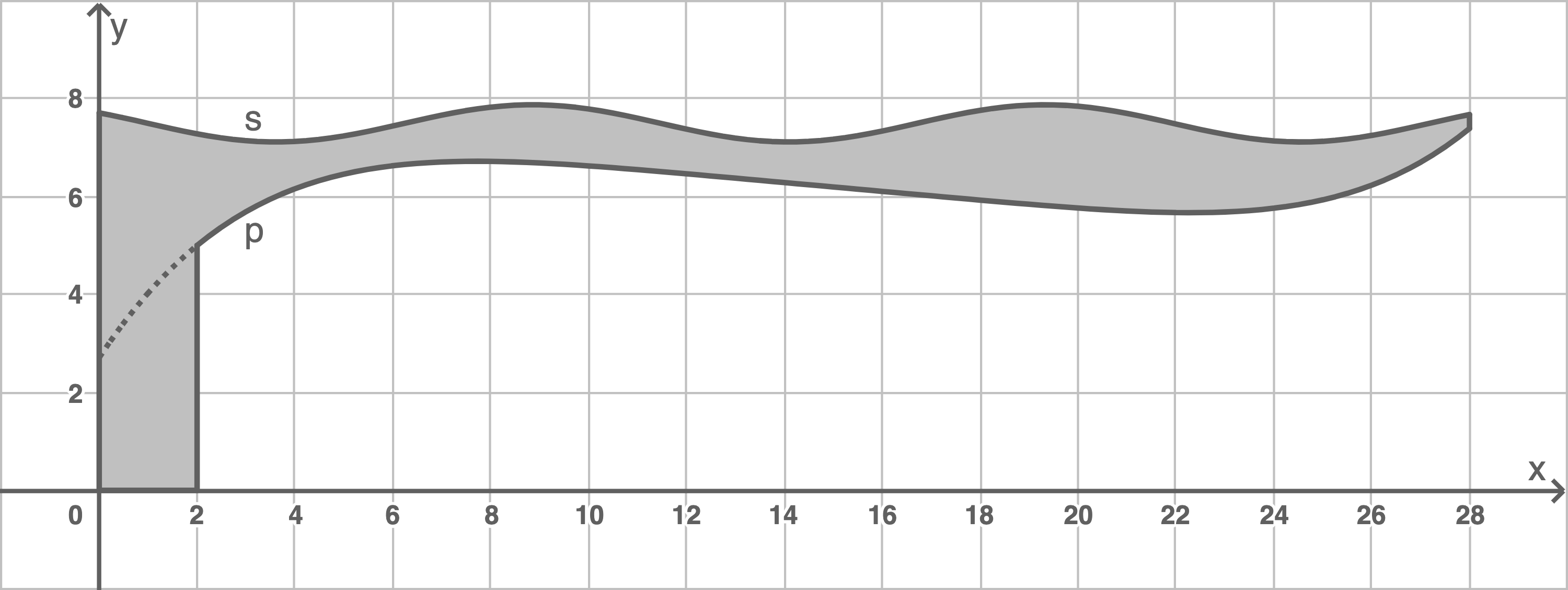
1.4.2

Der Radius des Bodens im Inneren der Vase entspricht dem Funktionswert von $p$ an der Stelle $x=2$ .

Durchmesser des Bodens im Inneren: $d _{ B }=2 \cdot p (2) \approx 10\,\text{cm}$

Der Radius der Standfläche entspricht dem Funktionswert von $s$ an der Stelle $x=0$ .

Durchmesser der Standfläche: $d_{s}=2 \cdot s(0) \approx 15,4\,\text{cm}$

1.4.3

Die Glasdicke $g$ kann an einer beliebigen Stelle $x$ durch die Differenz der Funktionswerte von $s$ und $p$ berechnet werden.

Somit ergibt sich als Funktion für die Glasdicke:

$g(x)=s(x)-p(x)$ $= -0,38\cdot \sin(0,6 (x - 1))$ $+ 7,5 - (0,008(0,24 (x - 15))^5$ $- 0,09 (x - 15) + 6,2)$

$g$ ist im Intervall $[2 ; 28]$ auf Maxima zu untersuchen:

$\(g$ mit $2 \leq x \leq 28$

Mit dem CAS folgen $x _{1} \approx 5,3;$ $x _{2} \approx 9,3;$ $x _{3} \approx 13,4;$ $x _{4} \approx 19,9$

Laut der gegebenen Abbildung kommen nur $g \left( x _{4}\right)$ bzw. die Dicke direkt über dem Innenboden als größte Glasdicke infrage.

Alternativ ergibt sich:

$\(g$ woraus ein Minimum folgt.

$\(g$ woraus ein Maximum folgt.

Vergleich der entsprechenden Funktionswerte an den Stellen liefert:

$g \left( x _{4}\right) \approx 2,1;$ $g (2)\approx 2,28$ (bzw. $g \left( x _{2}\right) \approx 1,2$ )

Somit beträgt die größte Glasdicke etwa 2,28 cm.

1.4.4

Abbildung (C) stellt den Sachverhalt dar.

Bei Betrachtung des vertikalen Abstands $g$ der Funktionen $s$ und $p$ anhand der gegebenen Abbildung ist zu erkennen:

$g$ nimmt direkt über dem Innenboden der Vase zunächst ab,
$g$ weist mehr als zwei (nämlich genau vier) lokale Extrema auf. (hier Argumentation auch mittels der Ergebnisse aus 1.4.3 möglich)

Abb. (A) kann ausgeschlossen werden, da hier der Graph zu Beginn ansteigt, was im Gegensatz zum Sachverhalt einer zunehmenden Glasdicke entsprechen würde.

Abb. (B) kann ebenfalls ausgeschlossen werden, da der Verlauf nur zwei lokale Extrema zeigt.

1.4.5

Die Vase wird als Rotationskörper (um die $x$ -Achse) modelliert.

Das Volumen ergibt sich als Differenz aus dem Volumen des Körpers, welcher durch Rotation der äußeren Funktion $s$ erzeugt wird und dem Innenvolumen des Körpers, welcher durch Rotation der inneren Funktion $p$ erzeugt wird:

$V =\pi \cdot\left(\underbrace{\displaystyle\int_{0}^{28}( s ( x ))^{2} dx }_{\text {Gesamtkörper }}-\underbrace{\displaystyle\int_{2}^{28}( p ( x ))^{2} dx }_{\text {Innenraum }}\right)$

Mit dem CAS ergibt sich $V\approx 1749\,\text{cm} ^{3}.$

Berechnung der Masse:

$m =\rho \cdot V =2,45 \dfrac{g}{\text{cm} ^{3}} \cdot 1749\,\text{cm} ^{3}$ $\approx 4285,1\,\text{g} \approx 4,3\,\text{kg}$

1.4.6

Der Stiel der Blume berührt den Graphen $P$ tangential im Punkt $Q.$ Die Tangente in $Q$ schließt mit der $x$ -Achse einen Winkel von $35^{\circ}$ ein, da $90^{\circ}-55^{\circ}=35^{\circ}$ . (s. Abb.)

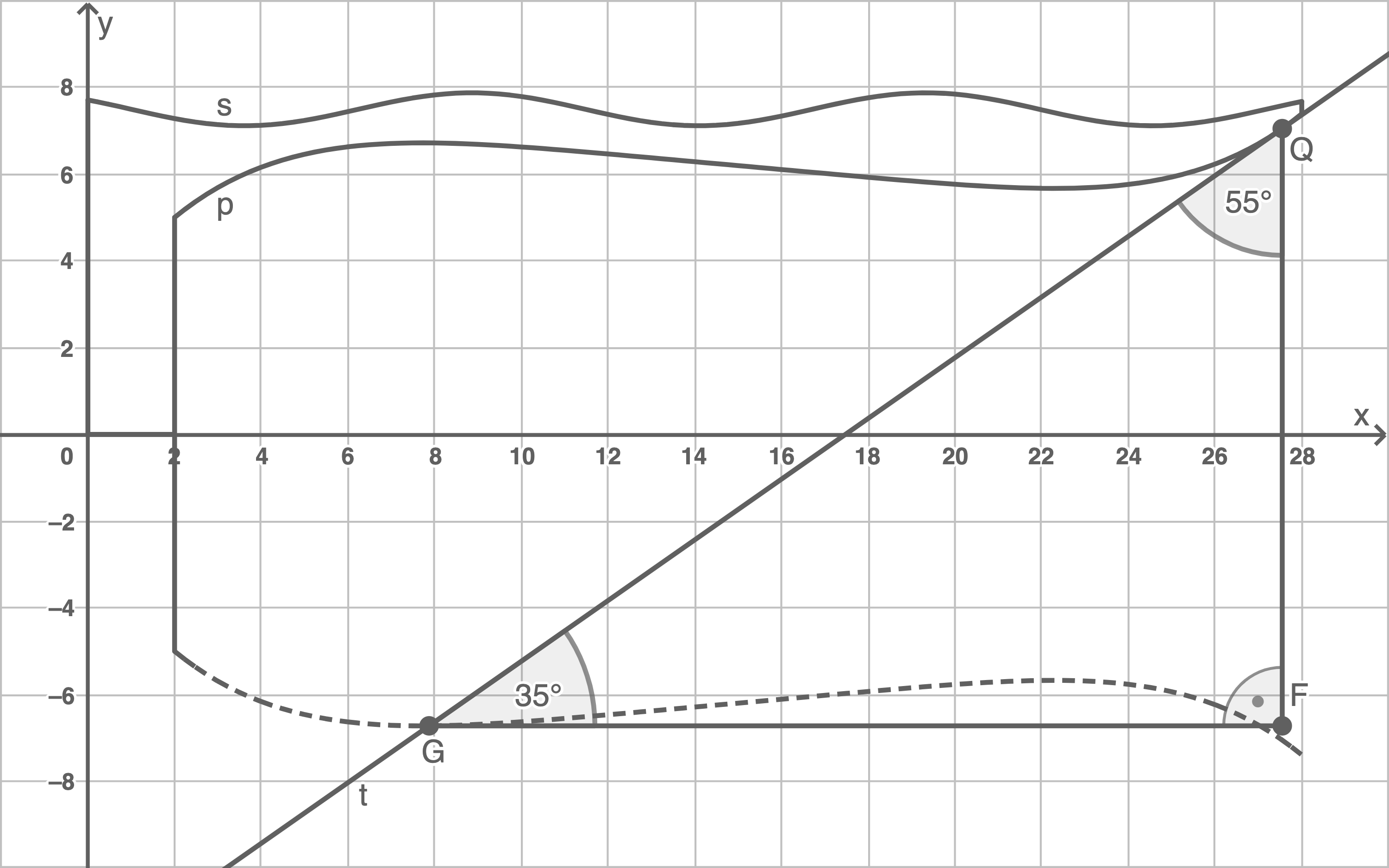Die Koordinaten folgen mit $G(x_3\mid -p(x_3))$ und $Q(x_2\mid p(x_2)).$

Ermittlung der Stelle $x$ , an welcher $P$ eine Steigung von $35^{\circ}$ aufweist:

$\(p$ $=\tan \left(35^{\circ}\right) \approx 0,7$

Mit dem solve-Befhel des CAS folgen $x _{1} \approx 2,45$ und $x_{2} \approx 27,55.$

$x_1$ entfällt, da in einer Höhe von $0,45\,\text{cm}$ über dem Boden der Blumenstiel die Vase nicht (tangential) berühren kann, wenn dessen Länge größer als die Höhe der Vase ist.

Tangente $t$ an der Stelle $x _{2}$ bzw. im Punkt $Q \left( x _{2} \mid p \left( x _{2}\right)\right)$ :

$p (27,55)=\tan \left(35^{\circ}\right) \cdot 27,55+ n$

Es ergibt sich $n \approx-12,2$ und daraus folgt die Gleichung der Tangente mit $t : y =0,7 \cdot x -12,2.$

Die Tangente $t$ schneidet den an der $x$ -Achse gespiegelten Graphen von $p$ im Punkt $G\left(x_{3} \mid p\left(x_{3}\right)\right)$ , wobei $x_{3}$ der Höhe über der Standfläche der Vase entspricht:

$- p \left( x _{3}\right)=0,7 \cdot x _{3}-12,2;$ $x _{3} \approx 7,8$

Abzüglich der Dicke des Vasenbodens ergibt sich: $7,8-2=5,8$

Bis etwa $6\,\text{cm}$ über dem Innenboden steht die Blume noch sicher in der Vase.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?