Teil A - Hilfsmittelfrei

Analysis - Pflichtaufgabe

Gegeben ist eine in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^4-k\cdot x^2$ , wobei $k$ eine positive reelle Zahl ist. Die Abbildung zeigt den Graphen von $f$ .

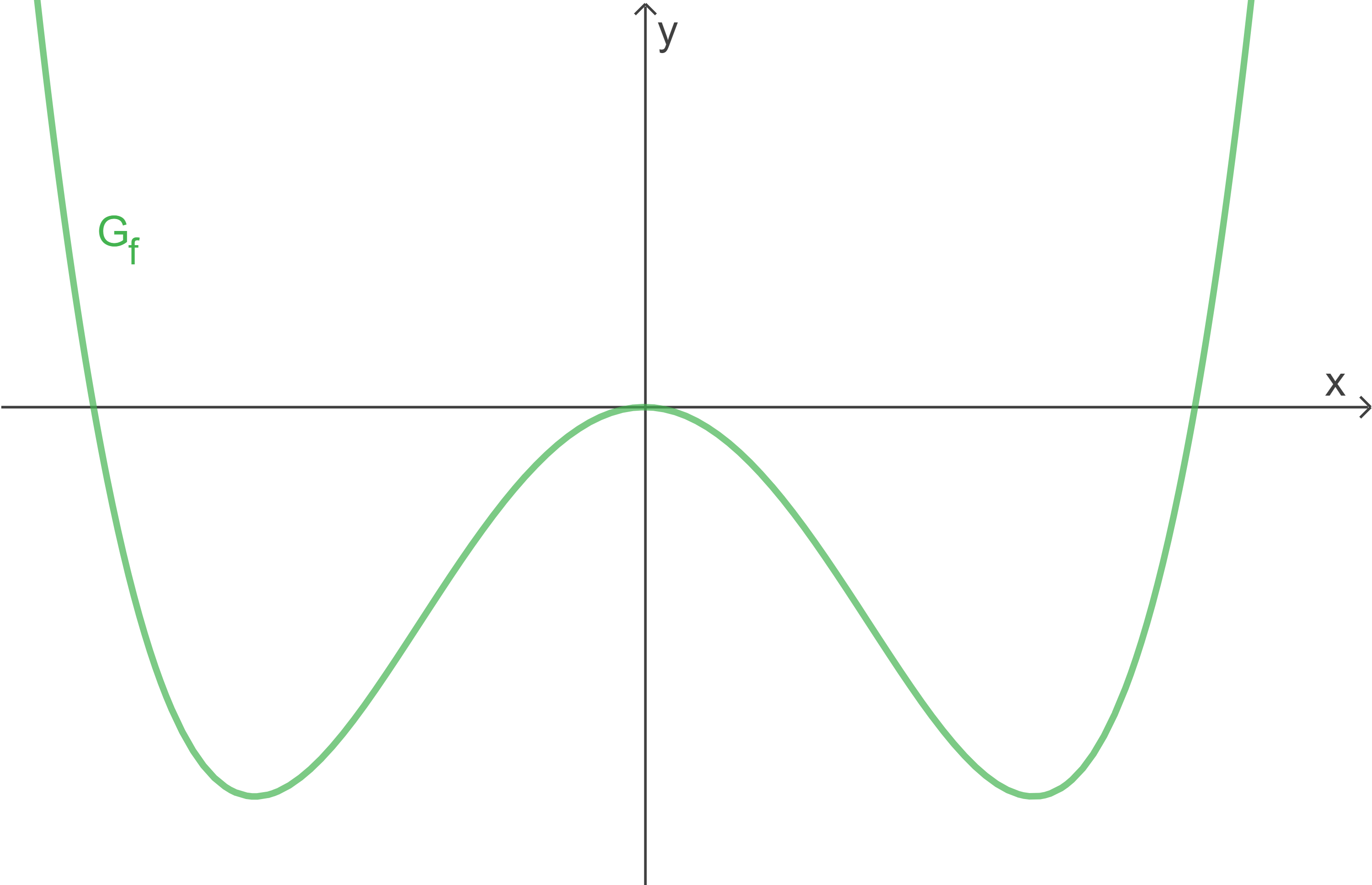
Graf einer Funktion mit x- und y-Achse, die eine geschwungene Kurve darstellt.

1.1

Zeige, dass $\(f$ eine Gleichung der ersten Ableitungsfunktion von $f$ ist.

(1 BE)

1.2

Die beiden Tiefpunkte des Graphen von $f$ haben jeweils die $y$ -Koordinate $-1$ .
Ermittle den Wert von $k$ .

(4 BE)

Analysis - Pflichtaufgabe

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=sin(x)$ .
Die Abbildung zeigt den Graphen $G_f$ von $f$ sowie die Tangenten an $G_f$ in den dargestellten Schnittpunkten mit der $x$ -Achse.

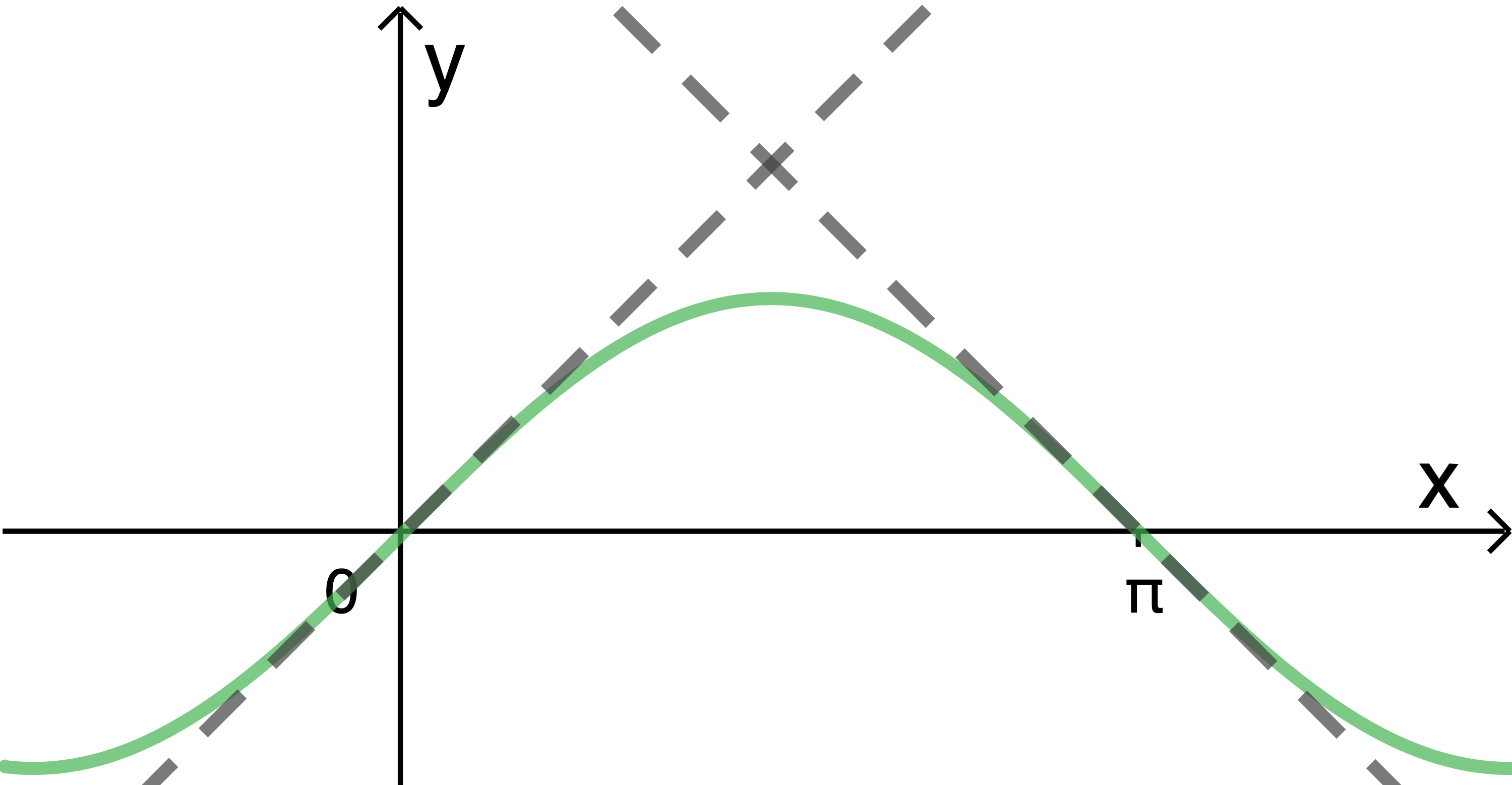
Graph einer mathematischen Funktion mit x- und y-Achse, zeigt eine sinusartige Welle und wichtige Punkte wie 0 und π.

2.1

Zeige, dass diejenige der beiden Tangenten, die durch den Koordinatenursprung verläuft, die Steigung $1$ hat.

(1 BE)

2.2

Berechne den Inhalt des Flächenstücks, das von $G_f$ und den beiden Tagenten eingeschlossen wird.

(4 BE)

Analytische Geometrie - Pflichtaufgabe

Gegeben sind die Punkte $A\left(2\mid-3\mid1\right)$ und $B\left(2\mid3\mid1\right)$ .

3.1

Begründe, dass die Gerade durch $A$ und $B$ parallel zur $y$ -Achse verläuft.

(1 BE)

3.2

Der Punkt $C$ liegt auf der $y$ -Achse. Die Gerade duch $A$ und $C$ steht senkrecht zur Gerade durch $B$ und $C$ .
Bestimme die Koordinaten aller Punkte, die die beschriebenen Eigenschaften des Punkts $C$ haben.

(4 BE)

Stochastik - Pflichtaufgabe

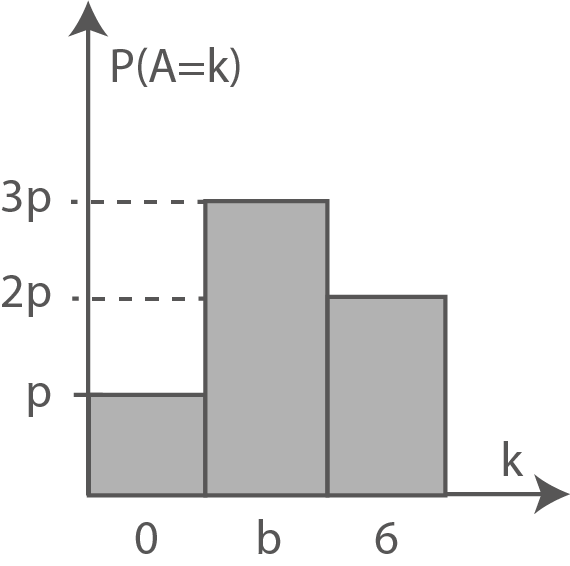
Bei einem Gewinnspiel beträgt der Einsatz für die Teilnahme $3 \; \text{Euro}$ . Die Auszahlung in $\text{Euro}$ wird durch die Zufallsgröße $A$ beschrieben. Die Abbildung zeigt die Wahrscheinlichkeitsverteilung von $A$ .

Balkendiagramm zur Darstellung der Wahrscheinlichkeiten P(A=k) in Abhängigkeit von k mit Achsen und Maßstab.

4.1

Zeige, dass $p$ den Wert $\frac{1}{6}$ hat.

(1 BE)

4.2

Bei wiederholter Durchführung des Spiels ist zu erwarten, dass sich auf lange Sicht Einsätze und Auszahlungen ausgleichen.
Berechne den Wert von $b$ .

(2 BE)

4.3

Beschreibe, wie das Gewinnspiel unter Verwendung eines Behälters sowie roter, grüner und blauer Kugeln durchgeführt werden könnte.

(2 BE)

Analysis - Wahlaufgabe

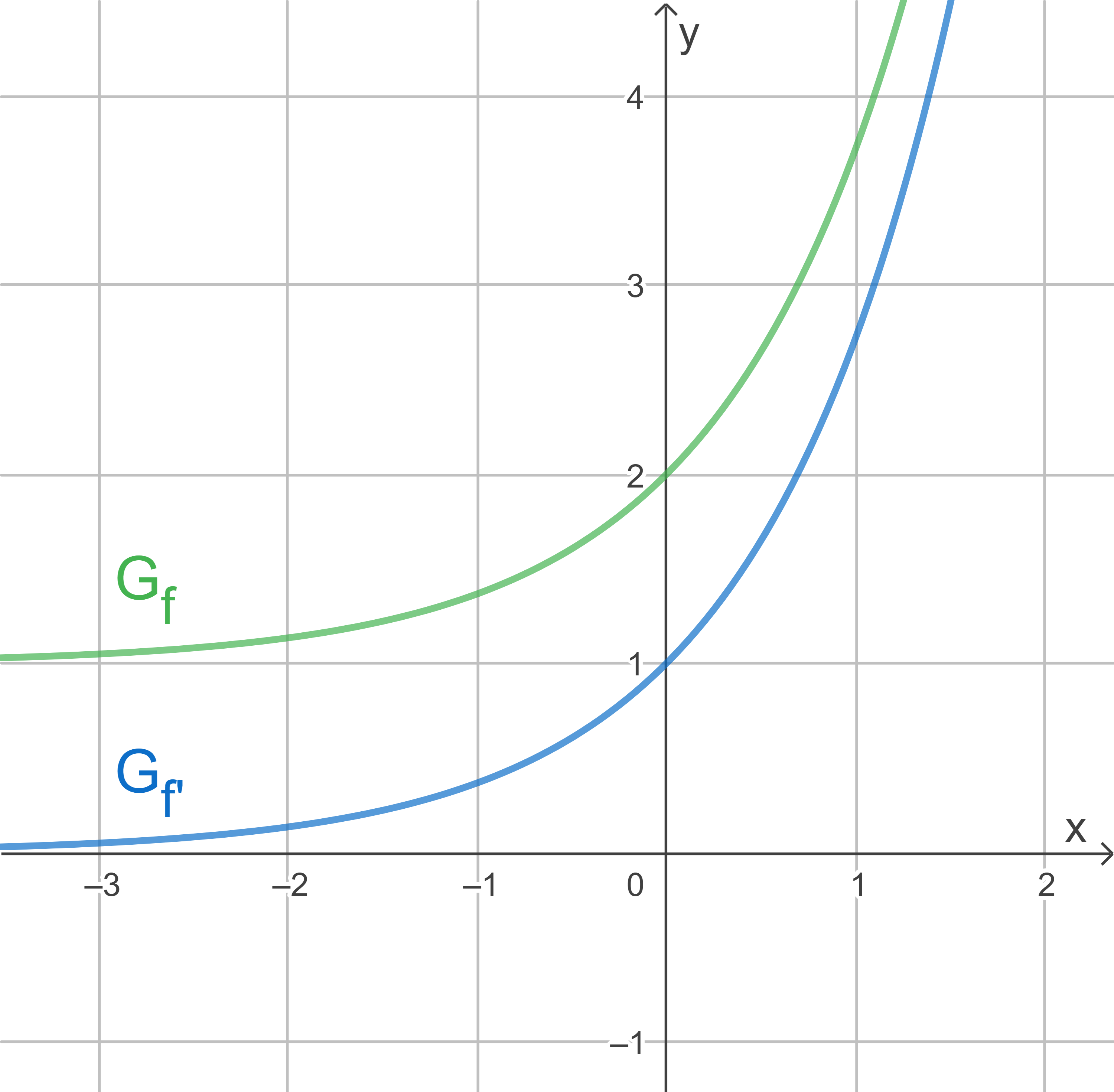
Die Abbildung zeigt den Graphen $G_f$ einer in $\mathbb{R}$ definierten Funktion $f$ sowie den Graphen der ersten Ableitungsfunktion von $f$ .

Graph zweier Funktionen Gf und Gf' im Koordinatensystem mit Achsenbeschriftung.

5.1

Gib die Steigung der Tangente an $G_f$ im Punkt $\left(0\mid f(0)\right)$ an.

(1 BE)

5.2

Betrachtet wird die Schar der Funktionen $g_c$ mit $c \in \mathbb{R}^+$ . Der Graph von $g_c$ geht aus $G_f$ durch Streckung mit dem Faktor $c$ in $y$ -Richtung hervor. Die Tangente an den Graphen von $g_c$ im Punkt $\left(0\mid g_c(0)\right)$ schneidet die $x$ -Achse.
Bestimme rechnerisch die $x$ -Koordinate des Schnittpunkts.

(4 BE)

Analytische Geometrie - Wahlaufgabe

Gegeben sind die Punkte $A\left(0\mid0\mid0\right)$ , $B\left(3\mid4\mid1\right)$ , $C\left(1\mid7\mid3\right)$ und $D\left(-2\mid3\mid2\right)$ .

6.1

Weise nach, dass das Viereck $ABCD$ ein Parallelogramm ist.

(1 BE)

6.2

Der Punkt $T$ liegt auf der Strecke $\overline{AC}$ . Das Dreieck $ABT$ hat bei $B$ einen rechten Winkel.
Ermittle das Verhältnis der Länge der Strecke $\overline{AT}$ zur Länge der Strecke $\overline{CT}$ .

(4 BE)

Stochastik - Wahlaufgabe

In einem Behälter befinden sich Kugeln, von denen jede dritte gelb ist.

7.1

Aus dem Behälter wird zweimal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. Berechne die Wahrscheinlichkeit dafür, dass beide Kugeln gelb sind.

(1 BE)

7.2

Im Behälter werden zwei gelbe Kugeln durch zwei blaue Kugeln ersetzt. Anschließend wird aus dem Behälter erneut zweimal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. Die Wahrscheinlichkeit dafür, dass beide Kugeln gelb sind, beträgt nun $\frac{1}{16}$ .
Ermittle, wie viele gelbe Kugeln sich nach den beschriebenen Vorgängen im Behälter befinden.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$\(\begin{array}[t]{rlll} f(x)&= & x^4-k\cdot x^2& \quad \scriptsize \\[5pt] f(x)$

Damit ist $\(f$ eine Ableitungsgleichung von $f(x)$ .

1.2

Durch die gegebene Abbildung ist das Extremum an der Stelle $x_1=0$ kein Tiefpunkt. Die Tiefpunkte sollen sein $\left(x_2\mid-1\right)$ und $\left(x_3\mid-1\right)$ .

1. Schritt: Mit der notwendigen Bedingung die x-Koordinaten der Tiefpunkte berechnen.

$x = \sqrt{\frac{k}{2}}$

Vollständige Lösung anzeigen

$x_2=\sqrt{\frac{k}{2}}$ und $x_3=-\sqrt{\frac{k}{2}}$

2. Schritt: Mit der Funktionsgleichung den Wert für $k$ bestimmen.

$k_{1,2}=\pm2$

Vollständige Lösung anzeigen

Mit $k \stackrel{!}{\gt} -1$ folgt, dass $k=2$ sein muss.

2.1

$\blacktriangleright$ Steigung der Funktion an $\left(0\mid0\right)$ berechnen.

$\(\begin{array}[t]{rlll} f(x)&=& sin(x) & \quad \scriptsize \\[5pt] f$

2.2

Du kannst das Flächenstück leicht berechnen, indem du die Symmetrie des Sinus und der gegebenen Tangenten ausnutzt.
Innerhalb der Grenzen von $0$ bis $\frac{\pi}{2}$ (Hochpunkt des Sinus) kannst du das Integral der Tangente von dem Integral des Sinus abziehen. Das so berechnete Teilstück ist symmetrisch bezüglich des Teilstücks in den Grenzen $\frac{\pi}{2}$ bis $\pi$ .

$2 \cdot \left(\int\limits_{0}^{\frac{\pi}{2}} x \,dx -\int\limits_{0}^{\frac{\pi}{2}} \sin(x) \,dx\right)$ $=\frac{\pi^2}{4}-2$

Vollständige Lösung anzeigen

3.1

Die Gerade durch $A$ und $B$ verläuft parallel zur y-Achse, weil $A\left(2\mid-3\mid1\right)$ und $B\left(2\mid3\mid1\right)$ beide die gleichen x- und z-Koordinaten haben.

3.2

Die Aufgabenstellung definiert den Punkt $C\left(0\mid c\mid 0\right)$ mit $c \in \mathbb{R}$ . Durch das gegebene Verhältnis der Geraden zueinander, kannst du über das Skalarprodukt $c$ bestimmen.

$c_{1,2} = \pm 2$

Vollständige Lösung anzeigen

Damit ergeben sich die Punkte $\left(0\mid-2\mid0\right)$ und $\left(0\mid2\mid0\right)$ .

4.1

$p=\frac{1}{6}$

Vollständige Lösung anzeigen

4.2

Du kannst der Abbildung entnehmen, dass $\frac{1}{6}$ der Teilnehmer $0$ €, $\frac{3}{6}$ der Teilnehmer $b$ € und $\frac{2}{6}$ der Teilnehmer $6$ € ausgezahlt bekommen. Daraus folgt als Gleichung:

$b=2$

Vollständige Lösung anzeigen

4.3

Um das Gewinnspiel mit farbigen Kugeln durchzuführen, müssen die Kugeln mit der selben Wahrscheinlichkeit gezogen werden. Im einfachsten Fall werden also $6$ Kugeln benötigt. Den Kugelfarben werden dabei die Auszahlungswerte zugeordnet.
Im Behälter befinden sich dann (zum Beispiel):

rote Kugel
- Es findet keine Auszahlung statt, wenn diese Kugel gezogen wird.
grüne Kugeln
- Es finden je $2$ € Auszahlung statt, wenn eine dieser Kugeln gezogen wird.
blaue Kugeln
- Es finden je $6$ € Auszahlung statt, wenn eine dieser Kugeln gezogen wird.

5.1

Die Steigung im Punkt $\left(0\mid f(0)\right)$ ist gleich $1$ , da die Ableitung der Funktion, welche die Steigung der Funktion beschreibt, an der Stelle $x=0$ durch den Punkt $\left(0\mid1\right)$ geht.

5.2

1. Schritt: Gleichung für das Verhältnis der Graphen zueinander aufstellen.
Für die y-Richtung gilt:

$\( g_c$ $= cx+2c$

Vollständige Lösung anzeigen

2. Schritt: x-Koordinate des Schnittpunkts berechnen.

$x=-2$

Vollständige Lösung anzeigen

6.1

Damit es ein Paralelogramm ist, müssen zwei Gegenseiten gleich groß und parallel sein. Das ist der Fall wenn ihre Vektoren einander entsprechen.

$\overline{AB}=\overline{DC}=\pmatrix{3\\4\\1}$

Vollständige Lösung anzeigen

6.2

1. Schritt: Den Ortsvektor von T bestimmen.
$T$ hat den Ortsvektor $\lambda \cdot \overline{AC}$
$T=\lambda \cdot \overline{AC}$ $=\lambda \cdot \pmatrix{1-0\\7-0\\3-0}$ $=\pmatrix{\lambda\\7\lambda\\3\lambda}$

2. Schritt: Das Skalarprodukt von $\overline{AB}$ und $\overline{TB}$ gleich $0$ setzen.
Das Skalarprodukt muss gleich $0$ sein, da die Aufgabenstellung für das Dreieck $ABT$ bei $B$ einen rechten Winkel fordert.
Daraus resultiert die Unterteilung der Strecke $AC$ in die Teilstrecken $\overline{AT}$ und $\overline{TC}$ .

$\lambda = \frac{13}{17}$

Vollständige Lösung anzeigen

Somit unterteilt der Punkt $T$ die Strecke $\overline{AC}$ nach $\lambda=\frac{13}{17}$ der Strecke, ausgehend von $A$ .

3. Schritt: Das Verhältnis von $\overline{AT}$ zu $\overline{CT}$ schlussfolgern.
Die Strecke wird im Verhältnis $13:4$ unterteilt.

7.1

Jede dritte Kugel ist gelb. Also folgt mit $p=\frac{1}{3}$ , dass die Wahscheinlichkeit zweimal eine gelbe Kugel zu ziehen $\frac{1}{3} \cdot \frac{1}{3}=\frac{1}{9}$ ist.

7.2

Jetzt ist jede vierte Kugel gelb. Wenn $x$ die gesuchte Anzahl ist, gilt:

$x=6$

Vollständige Lösung anzeigen

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?