1 Analysis

1.1

In einem Trainingszentrum absolvierte die Radsportlerin Alina eine $50$ Minuten dauernde Trainingseinheit auf einem Simulationsgerät. Dabei ist es mithilfe einer topographischen Datenbasis möglich, Steigung und Gefälle einer Strecke spürbar nachzustellen. Während dieser Trainingseinheit wurde eine Vielzahl von Messwerten erfasst, fünf Messwertpaare davon sind in der Tabelle aufgeführt.
Dabei ist $t$ die Zeit in Minuten und $s$ der zurückgelegte Weg in Kilometer.

$\color{#ffffff}{t}$	$\color{#ffffff}{s}$
$0$	$0$
$5,0$	$1,4$
$10,0$	$4,7$
$30,0$	$10,5$
$50,0$	$24,8$

Die Funktion $s$ mit

Funktionsterm anzeigen

$s(t)=...$

und $t \in \mathbb{R}$ ist im Intervall $0 \leq t \leq 50$ geeignet, die Trainingseinheit modellhaft darzustellen.

1.1.1

Weise nach, dass der Graph von $s$ durch den Koordinatenursprung verläuft und bestimme die Koordinaten der Wendepunkte dieses Graphen.

(Zur Kontrolle: $t_{W1} \approx 8,1 ; t_{W2} \approx 24,7 ; t_{W3} \approx 45,7)$

(4 BE)

1.1.2

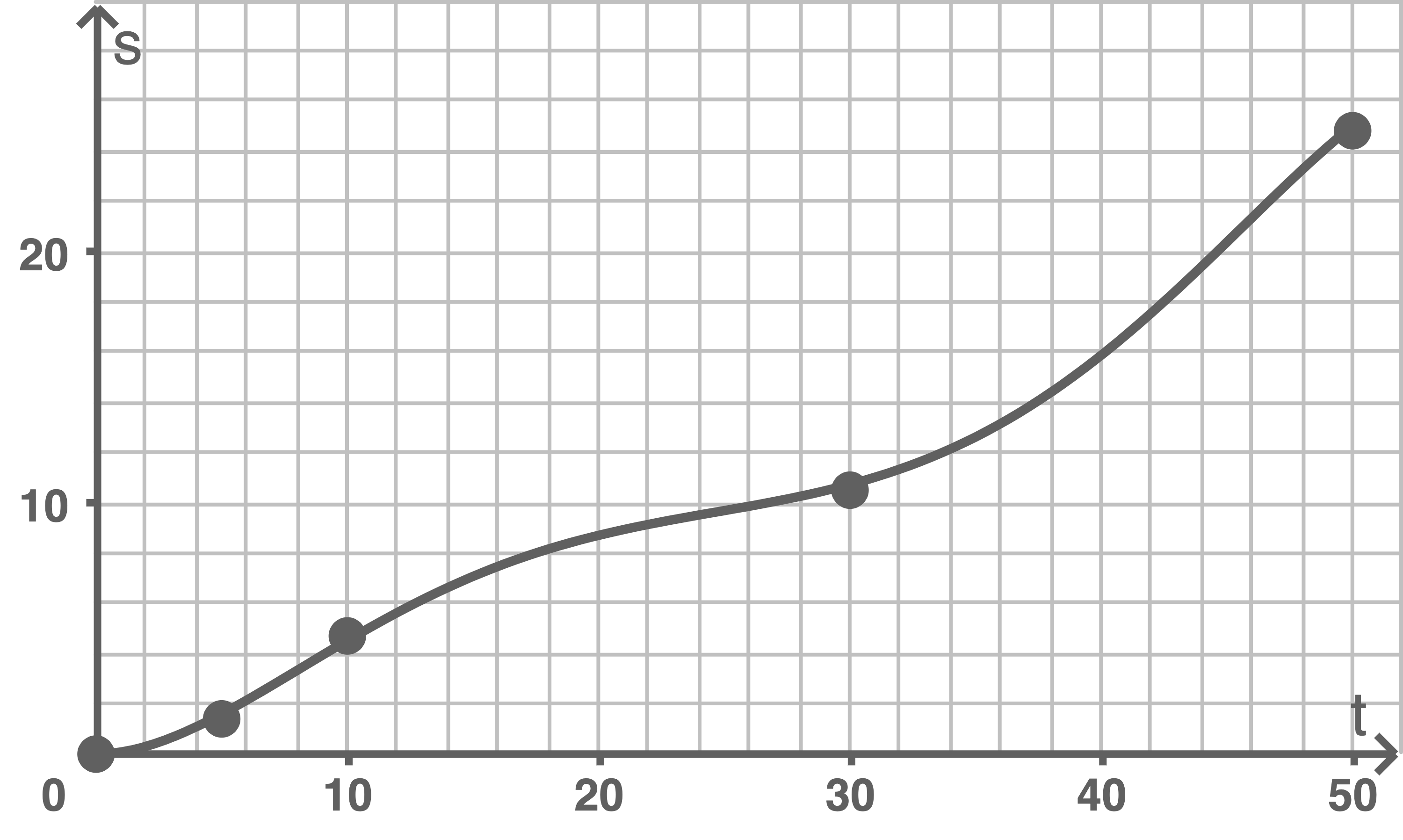
Zeichne den Graphen der Funktion $s$ im Intervall $0 \leq \mathrm{t} \leq 50$ und stelle die Messwerte von Alinas Trainingseinheit in diesem Diagramm dar.

(4 BE)

1.1.3

Berechne die Werte der Terme I und II.
Gib jeweils die Bedeutung der Terme im Sachzusammenhang an.

I $\quad \dfrac{s(30)-s(10)}{30-10}$

II $\quad \lim\limits_{t\to 5} \frac{s(5)-s(t)}{5-t}$

(4 BE)

1.1.4

Die Auswertung der Daten hat ergeben, dass während dieser Trainingseinheit eine Höchstgeschwindigkeit von etwa $58$ $\mathrm{km} / \mathrm{h}$ erreicht wurde. Zeige, dass das verwendete Modell ebenfalls diese Höchstgeschwindigkeit liefert.

(4 BE)

Für die Trainingseinheiten von Alina und einem weiteren Sportler Tom wurden die Momentangeschwindigkeiten während der Fahrt kontinuierlich erfasst und sind in Abbildung 1 dargestellt.

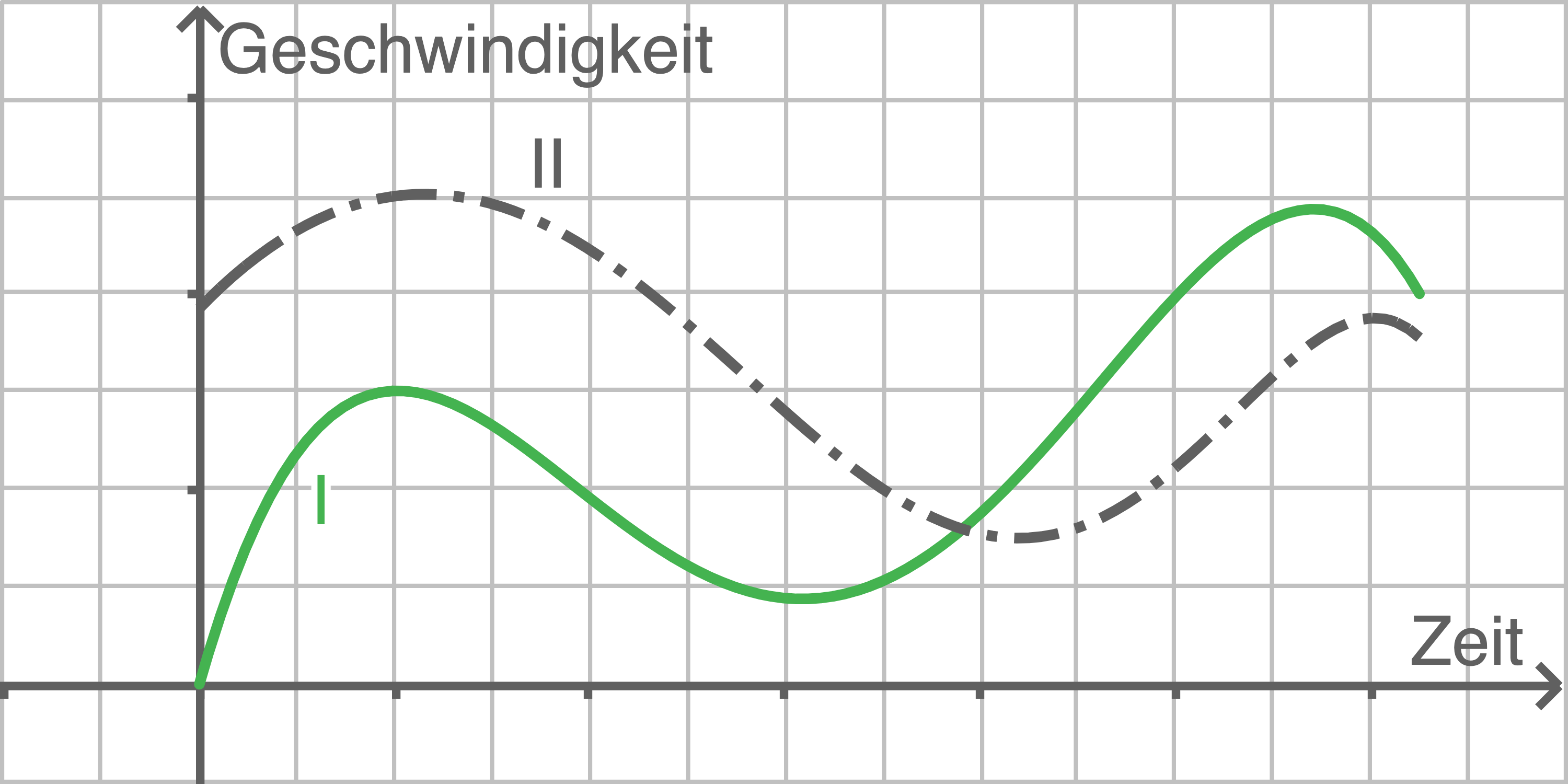
Geschwindigkeit Trainingseinheiten - Abi 2023

Abbildung 1

1.1.5

Erläutere anhand von zwei Eigenschaften des Graphen II, dass dieser Graph die Trainingseinheit von Alina nicht darstellen kann.

(4 BE)

1.1.6

Ergänze in Abbildung 1 die Skalierungen der Achsen und ermittle für die ersten $16$ Minuten von Toms Trainingseinheit die zurückgelegte Streckenlänge.

(5 BE)

1.2

Gegeben ist die für alle reellen Zahlen definierte Funktionenschar $f_k$ mit der Gleichung $f_k(x)=(x-k) \cdot(x+k) \cdot \mathrm{e}^{k-x}$ und $k \in \mathbb{R}, k>0$ .

1.2.1

Für jeden Wert von $k$ schließt der Graph von $f_{k}$ mit der $x$ -Achse im Intervall $[-k; k]$ die Fläche $A_k$ vollständig ein. Weiterhin existiert eine Fläche $B_k$ , deren Inhalt mit folgendem Term berechnet werden kann: $\lim\limits_{z\to \infty}\displaystyle\int_k^z f_k(x) \;\mathrm dx$
Weise nach, dass $B_k$ für jeden Wert von $k$ einen endlichen Flächeninhalt hat.
Zeige, dass es einen Wert $k$ gibt, sodass die Inhalte der Flächen $A_k$ und $B_k$ gleich groß sind.

(5 BE)

Die auf dem Graphen von $f_{\frac{1}{2}}$ liegenden Punkte $A\left(0 \mid f_{\frac{1}{2}}(0)\right)$ und $C\left(-\frac{1}{2} \mid 0\right)$ sind Eckpunkte des Vierecks $ABCD$ (vgl. Abbildung 2).

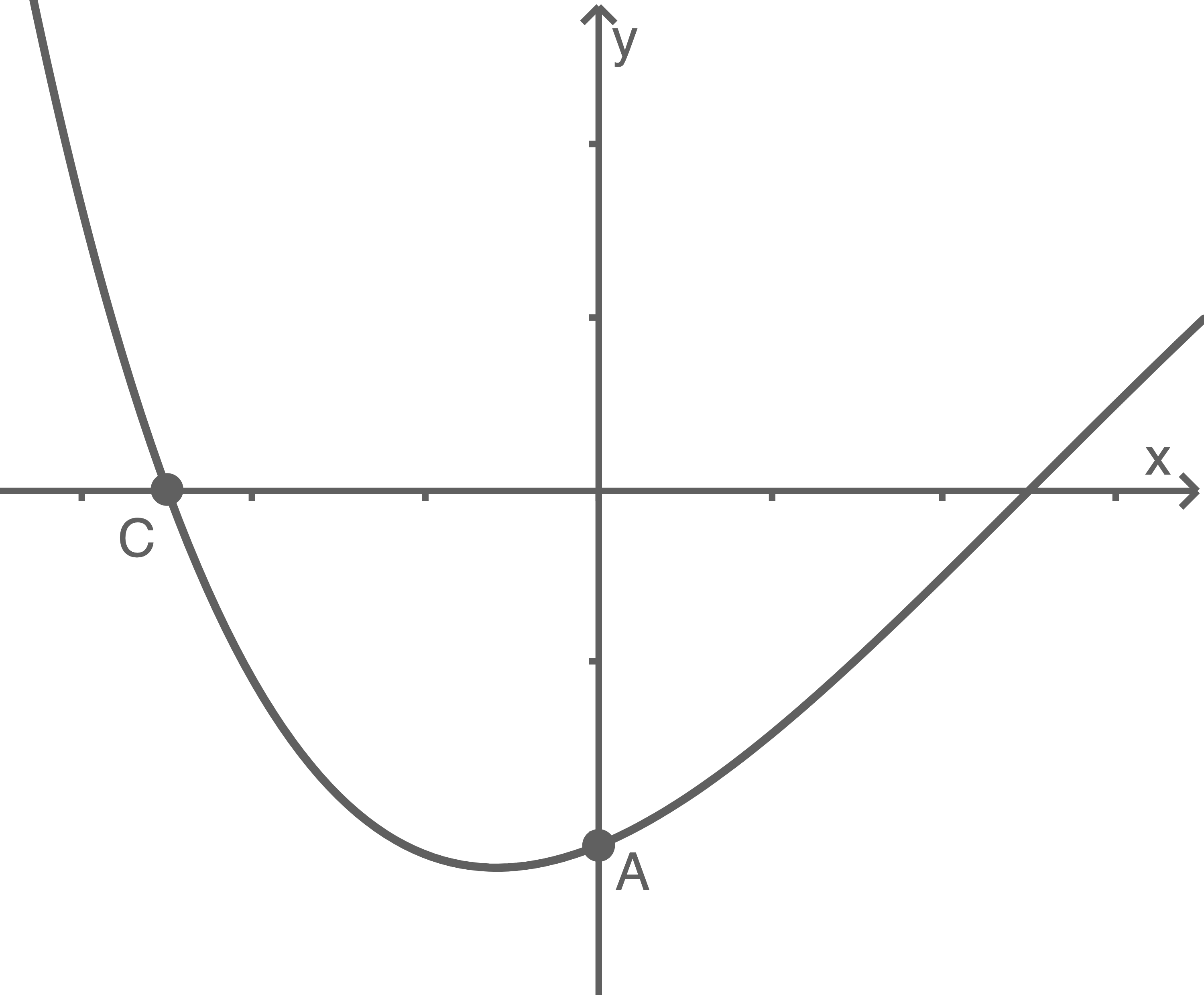
Abbildung 2

1.2.2

Die Punkte $B$ und $D$ liegen so, dass $A B C D$ ein Quadrat ist. Skizziere dieses Quadrat in Abbildung 2.

(2 BE)

1.2.3

Berechne für das Quadrat $A B C D$ die Koordinaten von $B.$

(6 BE)

1.2.4

Die Punkte $B_i$ und $D_i$ mit $i \in \mathbb{N}$ bilden gemeinsam mit $A$ und $C$ die Eckpunkte der Drachenvierecke $A B_i C D_i$ , bei denen die Seiten $\overline{A B_i}$ und $\overline{A D_i}$ gleich lang sind. Weiterhin besitzen diese Drachenvierecke rechte Winkel in den Punkten $B_i$ und $D_i$ . Beschreibe die Lage dieser Punkte $B_i$ und $D_i.$

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1.1

Verlauf des Graphen durch den Koordinatenursprung nachweisen

Rechenweg anzeigen

$s(0)=0$

Wegen $s(0)=0$ verläuft der Graph von $s$ durch den Koordinatenursprung.

Koordinaten der Wendepunkte bestimmen

Mit dem CAS kann die notwendige Bedingung für Wendestellen angewendet werden:

$\(s$ für

$t_1 \approx 8,1$

$t_2 \approx 24,7$

$t_3\approx 45,7$

Mit dem CAS kann die hinreichende Bedingung für Wendestellen überprüft werden:

$\(s$

Bei $t_1,$ $t_2$ und $t_3$ handelt es sich also um Wendestellen.

Mit dem CAS können die zugehörigen $y$ -Koordinaten berechnet werden:

$s(t_1)= s(8,1) \approx 3,4$

$s(t_2)= s(24,7) \approx 9,6$

$s(t_3)= s(45,7) \approx 21,0$

Die Koordinaten der Wendepunkte des Graphen von $s$ lauten:

$W_1(8,1\mid 3,4),$ $W_2(24,7\mid 9,6)$ und $W_3(45,7\mid 21,0)$

1.1.2

Funktion Trainingseinheit Radsportlerin Abi 2023

1.1.3

Mit dem CAS ergibt sich:

I $\quad \dfrac{s(30)-s(10)}{30-10} \approx 0,31$

II $\quad \lim\limits_{t\to 5}\dfrac{s(5)-s(t)}{5-t} \approx 0,53$

Term I stellt den Differenzenquotienten von $s$ im Intervall $[10 ; 30]$ und somit den Anstieg der Sekanten dar. Dieser entspricht der durchschnittlichen Geschwindigkeit in dem Zeitraum von 20 Minuten von $0,31 \frac{\text{km}}{\text{min}}.$

Term II stellt den Differenzenquotienten, also den Anstieg der Tangente an den Graphen von $s$ an der Stelle $t=5$ dar. Dieser Tangentenanstieg entspricht der Momentangeschwindigkeit von $0,53 \frac{\text{km}}{\text{min}}$ zum Zeitpunkt 5 Minuten nach Fahrtbeginn.

1.1.4

Die Geschwindigkeit zu einem Zeitpunkt $t$ wird durch den Wert der ersten Ableitung $\(s$ an der Stelle $t$ beschrieben.
Betrachtet werden also die Extremstellen von $\(s$ Diese entsprechen den Wendestellen von $s,$ da dort der Anstieg des Graphen von $s$ maximal bzw. minimal wird:

Mit dem CAS folgt:

$\(s$

Die höchste Geschwindigkeit ist also:

$0,97 \,\frac{\text{km}}{\text{min}} = 0,97 \cdot 60 \,\frac{\text{km}}{\text{h}} \approx 58 \,\frac{\text{km}}{\text{h}}$

1.1.5

Der Funktionsterm der ganzrationalen Funktion $s$ besitzt kein lineares Glied, folglich besitzt der Term der ersten Ableitungsfunktion $\(s$ kein Absolutglied (Konstante), weshalb für den Anstieg an der Stelle $t=0$ gilt: $\(s$
Graph II ist in seinem Schnittpunkt mit der $y$ -Achse eindeutig monoton steigend. Somit ist der Anstieg des Graphen II an der Stelle $t=0$ größer als $0.$

Aus Aufgabe 1.1.1 folgt, dass der zweite Wendepunkt des Graphen von $s$ an der Stelle $t \approx 24,7$ nahezu in der Mitte des betrachteten Intervalls $0 \leq t \leq 50$ liegt. Dies entspricht einem Extrempunkt des Graphen von $\(s$ Der Graph II hat seinen zweiten Extrempunkt allerdings erst deutlich nach der Hälfte des Intervalls.

1.1.6

Es wird der Bereich $0\leq t\leq 50$ betrachtet. In der Abbildung werden dafür $12,5$ Kästchen verwendet:

$50:12,5 = 4$

Auf der Zeitachse entspricht also ein Kästchen vier Minuten.

Laut 1.1.4 beträgt Alinas Höchstgeschwindigkeit $58\,\frac{\text{km}}{\text{h}} = 58:60 \,\frac{\text{km}}{\text{min}} \approx 0,97\,\frac{\text{km}}{\text{min}}$

Auf der Geschwindigkeitsachse entsprechen also fünf Kästchen einem $\frac{\text{km}}{\text{min}}.$

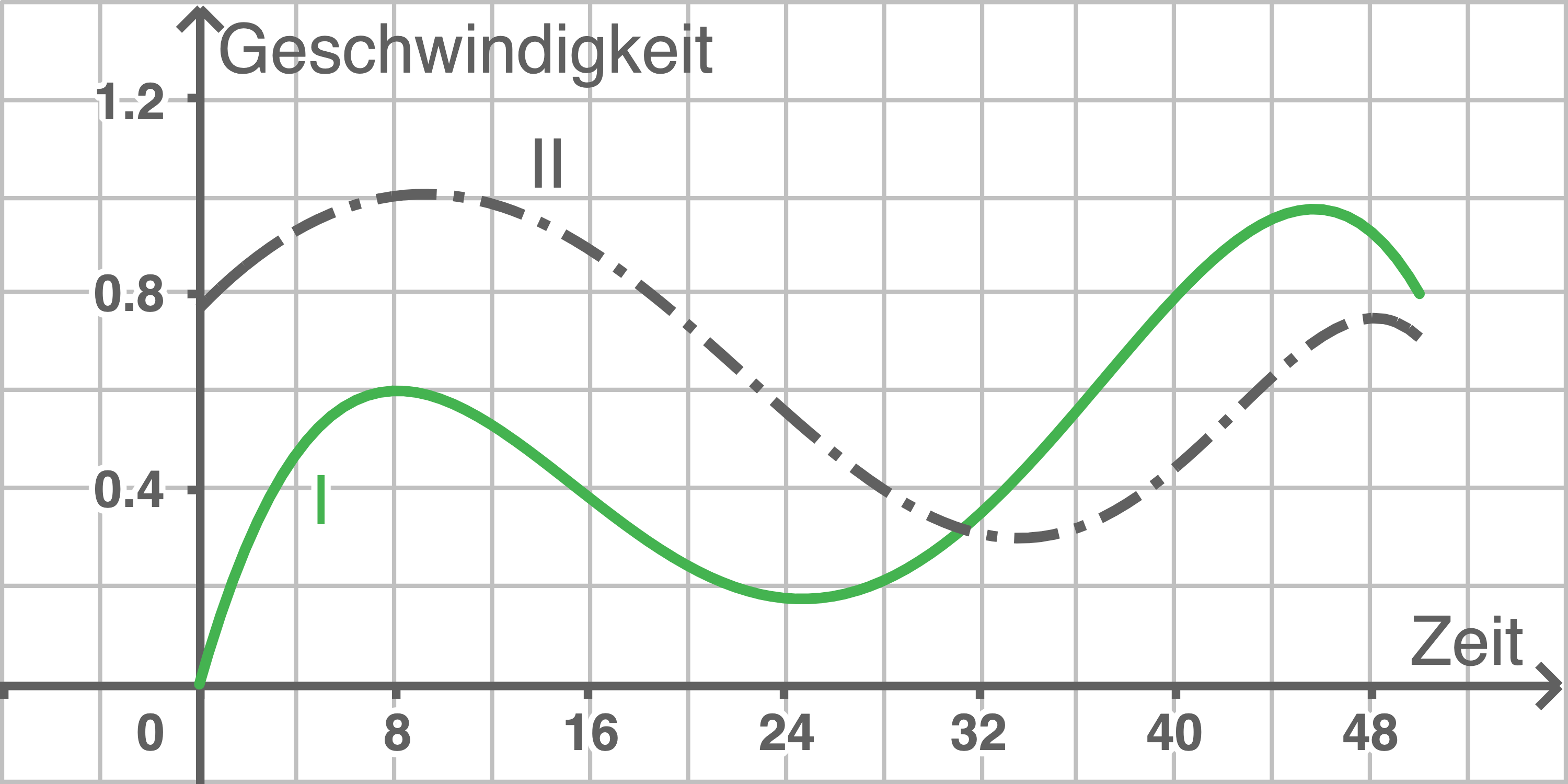Der Graph II und die Zeitachse schließen im Bereich $0 \leq t \leq 16$ ca. 18,5 Kästchen ein.

Es gilt: $18,5 \cdot 4 \;\text{min} \cdot 0,2 \frac{\text{km}}{\text{min}} = 14,8 \;\text{km}.$

Tom legt in den ersten 16 Minuten ca. $15 \;\text{km}$ zurück.

1.2.1

Endlichen Flächeninhalt nachweisen

Mit dem CAS folgt:

$\lim _{z \rightarrow \infty} \displaystyle \int_k^z f_k(x)\; \mathrm d x=2 \cdot(k+1)$

Somit ist der Flächeninhalt von $B_k$ für jeden Wert von $k$ endlich.

Zeigen, dass es einen Wert gibt, sodass beide Flächeninhalte gleich groß sind

Der Flächeninhalt von $A_k$ kann mit folgendem Term berechnet werden:

$\left| \displaystyle\int_{-k}^k f_k(x)\;\mathrm d x \right|$

Gleichsetzen mit dem Flächeninhalt von $B_k:$

$\left| \displaystyle\int_{-k}^k f_k(x)\;\mathrm d x \right|= 2\cdot (k+1)$

Mit dem CAS ergibt sich:

$k_1 \approx -0,82$

$k_2 =1$

Wegen $k\gt 0$ ist $k_2=1$ der gesuchte Wert.

1.2.2

Mögliches Vorgehen:

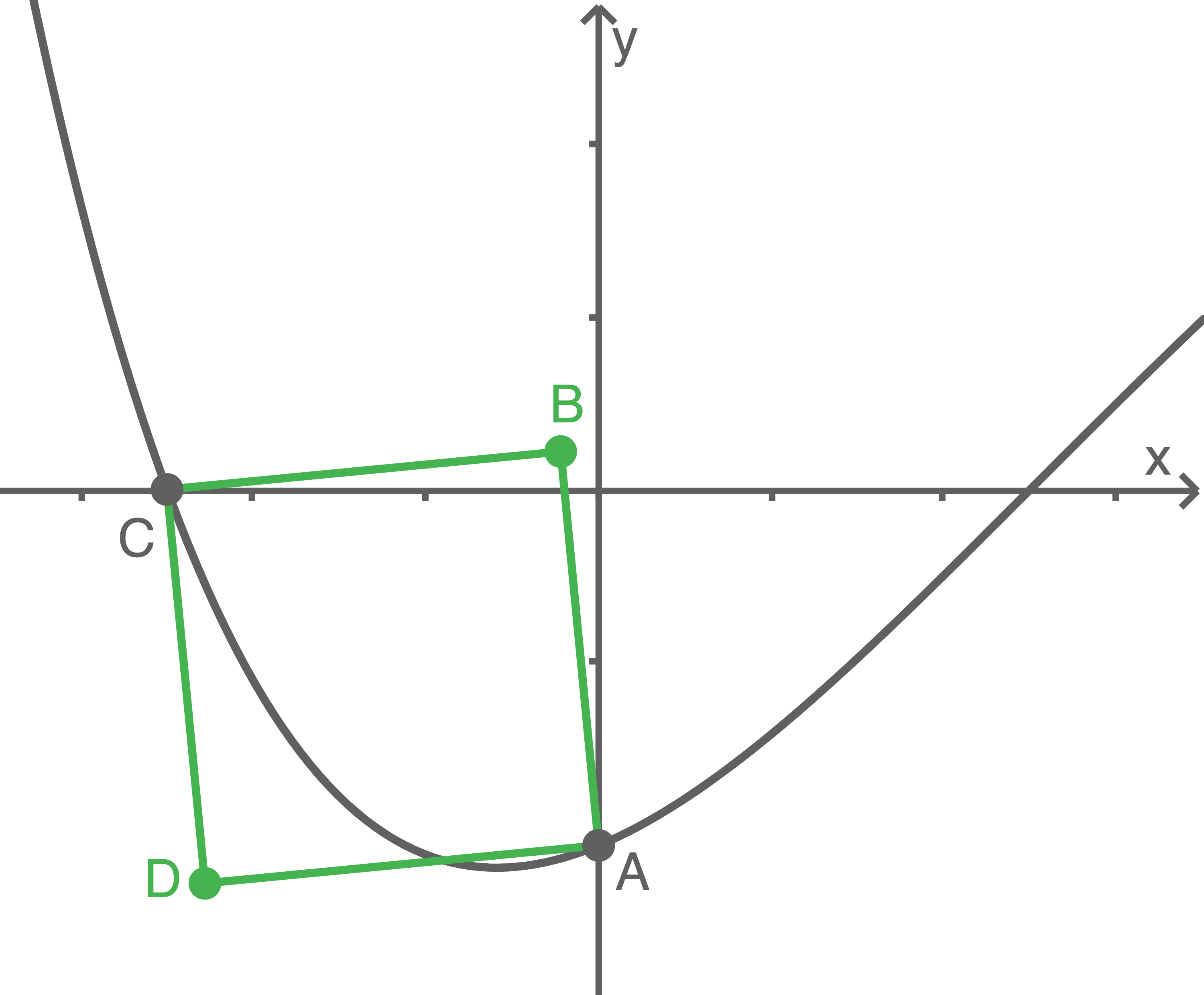
Einzeichnen der Gerade durch $A$ und $C$
Einzeichnen der Mittelsenkrechten von $\overline{AC}$
Einzeichnen einer Geraden, die die Gerade durch $A$ und $C$ im $45^{\circ}$ -Winkel im Punkt $C$ schneidet.
Der Schnittpunkt dieser Geraden mit der Mittelsenkrechten ist entweder der Punkt $B$ oder der Punkt $D.$
Der zweite Punkt kann durch Spiegelung eingezeichnet werden.

1.2.3

Die Steigung der Geraden durch $A$ und $C$ lässt sich wie folgt berechnen:

$\frac{f_{\frac{1}{2}}(0)-f_{\frac{1}{2}}\left(-\frac{1}{2}\right)}{0-\left(-\frac{1}{2}\right)}=-\frac{\mathrm e^{\frac{1}{2}}}{2}$ .

Da sich die Diagonalen eines Quadrats senkrecht schneiden, muss die Gerade durch $B$ und $D$ senkrecht dazu verlaufen. Ihre Steigung entspricht also der Normalensteigung:

$-\frac{1}{-\frac{\mathrm e^{\frac{1}{2}}}{2}}=2 \cdot \mathrm e^{-\frac{1}{2}}$

Die beiden Geraden schneiden sich im Mittelpunkt der Strecke $\overline{AC}.$ Die Schnittstelle liegt daher in der Mitte des Intervalls $\left[-\frac{1}{2} ; 0\right]$ und beträgt $x_s=-\frac{1}{4}.$

Die $y$ -Koordinate entspricht dem Mittelwert der $y$ -Koordinaten der Punkte $A$ und $C:$

$\frac{f_{\frac{1}{2}}(0)+f_{\frac{1}{2}}\left(-\frac{1}{2}\right)}{2}=-\frac{\mathrm e^{\frac{1}{2}}}{8} \approx-0,21.$

Somit hat der Schnittpunkt die Koordinaten $\mathrm{S}\left(-\frac{1}{4} \mid-0,21\right).$

Als Gleichung der Geraden durch die Punkte $B$ und $D$ folgt:

Rechenweg anzeigen

$c = \frac{\mathrm e^{-\frac{1}{2}}}{2}-\frac{\mathrm e^{\frac{1}{2}}}{8}$

Also ist $y_N(x)=2 \cdot \mathrm e^{-\frac{1}{2}} \cdot x+\frac{1}{2} \cdot \mathrm e^{-\frac{1}{2}}-\frac{1}{8} \cdot \mathrm e^{\frac{1}{2}}$

Gesucht ist der Punkt $B\left(x \mid y_N(x)\right)$ auf der Geraden $y_N,$ der zum Punkt $S$ den gleichen Abstand besitzt wie Punkt $A:$

Rechenweg anzeigen

$\begin{array}[t]{rll} |\overline{\mathrm{AS}}|&=& |\overline{\mathrm{BS}}| \\[5pt] & ... & \\[5pt] x_1 &=& \frac{\mathrm{e}^{\frac{1}{2}}-2}{8} \\[5pt] x_2 &=& -\frac{\mathrm{e}^{\frac{1}{2}}-2}{8} \end{array}$

$x_2$ entspricht der $x$ -Koordinate von $D.$

Mit $\mathrm{y}_{\mathrm{N}}\left(\frac{\mathrm{e}^{\frac{1}{2}}-2}{8}\right)=\frac{1}{4}-\frac{\mathrm{e}^{\frac{1}{2}}}{8}$ folgt daher:

$\mathrm{B}\left(\frac{\mathrm{e}^{\frac{1}{2}}-2}{8} \mid \frac{1}{4}-\frac{\mathrm{e}^{\frac{1}{2}}}{8}\right)$

1.2.4

Die Punkte $B_i$ und $D_i$ liegen auf dem Kreis um den Punkt $S$ mit dem Radius $|\overline{\mathrm{SA}}|.$ Dadurch wird zum einen die Bedingung erfüllt, dass die Punkte $B_i$ und $D_i$ den gleichen Abstand zu $A$ haben, da $A$ ebenfalls auf dem Kreis liegt. Zum anderen folgt mit dem Satz des Thales, dass die Winkel in diesen beiden Punkten rechte Winkel sind.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?