Lerninhalte in Mathe

Abi-Aufgaben LK (WTR)

Abi-Aufgaben LK (CAS)

Digitales Schulbuch

Inhaltsverzeichnis

Wahlteil B1

B1 Analysis und Stochastik

In einem kartesischen Koordinatensystem wird eine Fläche durch die Graphen der Funktion $f$ und $a$ , die $x$ -Achse sowie die Geraden $x_1=-1$ und $x_2 = k$ ( $k \gt 0$ ) begrenzt.

Es gilt $f(x) =1,3\sqrt{x}$ und $a(x)= -0,001x^3-0,002x^2+0,35x +2$ mit $k,x \in \mathbb{R}$ .

Diese Fläche erzeugt bei der Rotation um die $x$ -Achse einen Körper.

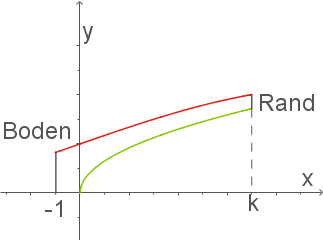
Grafik eines Koordinatensystems mit einer roten und einer grünen Kurve sowie beschrifteten Achsen.

Abb. 1

Hierbei stellen im Achsenschnitt (siehe Abb. 1) der Graph von $f$ die Innenwand und der Graph von $a$ die Außenwand eines Glases dar. Die Geraden bilden den Boden bzw. den oberen Rand des Glases.

Die Dicke der Glaswand wird für $x \gt 0$ zwischen Außen- und Innenwand parallel zum Boden gemessen; die Höhe vom Boden aus. Dabei entspricht eine Einheit einem Zentimeter.

Um Isoliergläser herzustellen, wird der Raum, den die rotierende Fläche erzeugt, evakuiert.

1.1

Ermittle den Innendurchmesser des Glases in einer Höhe von $6\,\text{cm}$ .
Berechne die Höhe des Glases unter Voraussetzung, dass der Rand etwa $2\,\text{mm}$ stark ist.
Weise nach, dass die Dicke der Glaswand von unten nach oben betrachtet ständig geringer wird.

1.2

Dieses etwa $11\,\text{cm}$ hohe Glas soll zu zwei Dritteln des möglichen Gesamtvolumens mit Flüssigkeit gefüllt werden.
Ermittle, wie weit die Flüssigkeit unterhalb des Randes steht.
Berechne die Größe des evakuierten Raumes.

1.3

In der Höhe von $8,5\,\text{cm}$ wird zur Verzoerung ein Schliff parallel zum Boden rund um das Glas ausgeführt. Drei weitere Schliffe führen von diesem ersten aus senkrecht bis zum Boden.
Berechne die Zeit zum Anbringen aller dieser Verzierungen, wenn für $1\,\text{cm}$ etwa $6$ Sekunden benötigt werden.

1.4

Man weiß aus Erfahrung, dass bei der Produktion dieser Isoliergläser fehlerhafte Produkte mit einer Wahrscheinlichkeit von etwa $1,5\,\%$ auftreten. Eine Tagesproduktion umfasst $2.000$ Gläser.

1.4.1

Gib den Erwartungswert an und berechne die Standardabweichung für die zufällige Anzahl fehlerhafter Gläser in einer Tagesproduktion.

1.4.2

Ermittle die Höchstzahl fehlerhafter Gläser in der Tagesproduktion, bis zu der man mit einer Irrtumswahrscheinlichkeit von $5\,\%$ noch davon ausgehen kann, dass sich die Fehlerquote nicht erhöht hat.

Bildnachweise [nach oben]

[1]

© 2017 - SchulLV.

B1 Analysis und Stochastik

1.1

$\blacktriangleright$ Innendurchmesser ermitteln

Gesucht ist der Innendurchmesser des Glases in einer Höhe von $6\,\text{cm}$ . Der Verlauf der Innenwand wird durch die Funktion $f$ beschrieben. Die Höhe wird vom Boden aus gemessen, der durch die Gerade $x_1 = -1$ modelliert wird. Die Höhe des Glases von $6\,\text{cm}$ befindet sich also an der Stelle $x = 6-1 = 5$ . Berechne also $f(5)$ :

$f(5) = 1,3\cdot \sqrt{5}$

Da der Durchmesser gesucht ist, musst du den Radius noch verdoppeln:

$2\cdot 1,3\cdot \sqrt{5} \approx 5,81\,\text{[cm]}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

In einer Höhe von $6\,\text{cm}$ besitzt das Glas einen Innendurchmesser von ca. $5,81\,\text{cm}$ .

$\blacktriangleright$ Höhe des Glases berechnen

Für die Dicke des Randes gilt $d(x)= a(x)- f(x)$ . Berechne den Wert für $x$ für welchen $d(x)=0,2$ ist:

$x=9,94~\text{cm}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Auch hier musst du wieder $1~\text{cm}$ dazurechnen, da der Boden bei $x=-1$ anfängt.
Somit ist das Glas $10,94 \,\text{cm}$ hoch.

$\blacktriangleright$ Verlauf der Glaswand nachweisen

Du sollst nachweisen, dass die Dicke der Glaswand von unten nach oben hin immer geringer wird. Die Dicke wird für $x \gt 0$ parallel zum Boden gemessen. Sie wird durch den Abstand zwischen den beiden Funktionsgraphen $a$ und $f$ modelliert. Den Abstand an der Stelle $x$ kannst du mit der Differenz $d$ der beiden Funktionen beschreiben. Der Abstand wird immer geringer, wenn der Graph von $d$ streng monoton fallend ist. Dies kannst du mit Hilfe der ersten Ableitung $d‘$ überprüfen. Ist diese kleiner als Null für alle $x \gt 0$ , dann ist der Graph von $d$ streng monoton fallend.

$\begin{array}[t]{rll} d(x)&=& -0,001x^3... \\[10pt] d‘(x)&=&-0,003x^2... \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Überprüfe nun, für welche $x$ $d‘(x) \lt 0$ gilt. Dazu kannst du den solve-Befehl deines CAS verwenden.

Du erhältst folgende Lösung:

$x \gt 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

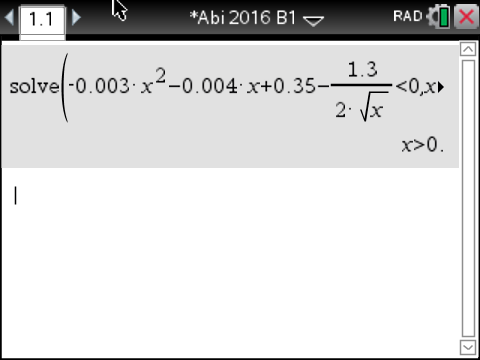Mathematische Gleichung zur Lösung in einem grafischen Taschenrechner dargestellt.

Abb. 1: Ungleichung lösen

Für alle $x \gt 0$ ist also $d‘(x) \lt 0$ , also ist die Differenz der beiden Funktionen $a$ und $f$ streng monoton fallend. Da diese die Dicke der Glaswand beschreibt, nimmt die Dicke von unten nach oben betrachtet immer weiter ab.

1.2

$\blacktriangleright$ Füllhöhe ermitteln

Du sollst ermitteln, wie weit die Flüssigkeit unterhalb des Rands steht. Das Glas ist zu zwei Dritteln des Gesamtvolumens gefüllt. Der Teil des Glases, der gefüllt werden kann, wird durch die Innenwand begrenzt. Das Gesamtvolumen ergibt sich also als Rotationsvolumen des Graphen von $f$ .
Du kannst also wie folgt vorgehen:

Berechne das Gesamtvolumen an Flüssigkeit, die in das Glas passt, mit Hilfe eines Rotationsvolumens. Das Volumen der eingefüllten Flüssigkeit beträgt zwei Drittel des Gesamtvolumens.
Setze das Volumen der eingefüllten Flüssigkeit in die Formel für das Rotationsvolumen ein. Die Gleichung kannst du dann nach der oberen Grenze lösen und erhältst so den Füllstand des Glases.

1. Schritt: Volumen der Flüssigkeit berechnen

Das Innere des Glases kann durch einen Rotationskörper des Graphen von $f$ um die $x$ -Achse dargestellt werden. Ein solches Rotationsvolumen kannst du mit folgender Formel berechnen:

$V_x = \pi \cdot \displaystyle\int_{a}^{b}\left( f(x)\right)^2 \;\mathrm dx$

Für die untere Grenze musst du $a=0$ einsetzen, da der innere Rand des Glases bei $x=0$ beginnt.
Das Glas ist $11\,\text{cm}$ hoch. Die Höhe wird aber vom Boden an gemessen, der durch die Gerade $x_1 = -1$ beschrieben wird. Der obere Rand des Glases befindet sich daher an der Stelle $b = 10$ .

Das Integral kannst du mit deinem CAS berechnen. Den Befehl dafür findest du wie folgt:

menu $\to$ 4: Analysis $\to$ 3: Integral

$V_{\text{Gesamt}} = \pi \cdot 84,5 \,\text{[VE]}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das Volumen der eingefüllten Flüssigkeit ist also $V_{\text{Flüssigkeit}} = \frac{169}{3}\cdot \pi$

2. Schritt: Gleichsetzen

Gesucht ist nun die obere Grenze $b$ des Rotationsvolumens mit $V_{\text{Flüssigkeit}} = \frac{169}{3}\cdot \pi$ .

$\begin{array}[t]{rll} \pi \cdot \displaystyle\int_{0}^{b}\left( f(x)\right)^2 \;\mathrm dx &=& ... \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Löse diese Gleichung mit dem solve-Befehl deines CAS nach $b$ . Du erhältst dann die Lösungen $b_1 \approx 8,16$ und $b_2\approx -8,16$ , wobei $b_2$ wegfällt, da nur der Bereich $x \gt 0$ betrachtet wird.

Da sich der Rand bei $x =10$ befindet, ist die Flüssigkeit also bis ca. $1,84\,\text{cm}$ unterhalb des Randes gefüllt.

$\blacktriangleright$ Größe des evakuierten Raumes berechnen

Der Raum, der evakuiert werden soll, entsteht aus dem Rotationskörper des Graphen von $a$ um die $x$ -Achse im Bereich $a_1 = -1$ und $b = 10$ , aus dem der Rotationskörper des Graphen von $f$ im Bereich $a_2 = 0$ und $b$ herausgelöst wird.

Das Volumen des inneren Teils hast du bereits berechnet. Das Volumen des äußeren Teils kannst du mit der gleichen Formel berechnen.

$V_{\text{außen}} \approx 396,41$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das Volumen des evakuierten Raumes ergibt sich damit wie folgt:

$V_{\text{Evakuiert}} \approx 130,96$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der evakuierte Raum hat eine Größe von ca. $130,96\,\text{cm}^2$ .

1.3

$\blacktriangleright$ Zeit zum Anbringen der Verzierungen berechnen

Um die Zeit zu berechnen, die für alle Verzierungen benötigt wird, musst du die Gesamtlänge aller Verzierungen berechnen. Diese setzt sich zusammen aus zwei Arten von Schliffen:

Der Schliff rund um das Glas:
Die Länge ist der Umfang eines Kreises, dessen Radius der Funktionswert von $a$ an der entsprechenden Stelle ist.
Die drei Schliffe senkrecht zum Boden: Diese Schliffe verlaufen entlang der Außenwand. Sie besitzen die gleiche Länge, die über die Bogenlänge des Graphen von $a$ im entsprechenden Intervall berechnet werden kann. Dazu kann folgende Formel verwendet werden:

$s = \displaystyle\int_{a}^{b}\sqrt{1+ \left[f‘(x)\right]^2}\;\mathrm dx$

1. Schritt: Länge des ersten Schliffs berechnen

Da die Höhe des Glases vom Boden aus gemessen wird und dieser bei $x_1 = -1$ liegt, kannst du den Radius des Glases in der Höhe $8,5\,\text{cm}$ über $a(7,5)$ berechnen.

$a(7,5) \approx 4,09$

Damit kannst du nun den Umfang des Glases berechnen:

$\begin{array}[t]{rll} U&=&2\cdot \pi \cdot r \\[5pt] &=& 2\cdot \pi \cdot a(7,5) \\[5pt] &\approx& 2\cdot \pi \cdot 4,09 \,\text{cm}\\[5pt] &\approx& 25,70 \,\text{cm} \end{array}$

Der erste Schliff ist ca. $25,70\,\text{cm}$ lang.

2. Schritt: Länge der senkrechten Schliffe berechnen

Die Länge der senkrechten Schliffe kannst du über die Bogenlänge des Graphen von $a$ berechnen. Die Schliffe laufen senkrecht vom ersten Schliff nach unten zum Boden. Du benötigst also die Bogenlänge von $a = -1$ bis $b = 7,5$ .
Das Integral kannst du wieder mit deinem CAS berechnen:

$s \approx 8,86$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einer der drei senkrechten Schliffe ist also ca. $8,86\,\text{cm}$ lang.

Insgesamt ergibt sich also folgende Gesamtlänge aller Schliffe:

$S = 52,28\,\text{cm}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

3. Schritt: Benötigte Zeit berechnen

Für $1\,\text{cm}$ werden ca. $6$ Sekunden benötigt. Die Schliffe haben insgesamt eine Länge von ca. $52,28\,\text{cm}$ . Es ergibt sich dann folgende Zeit:

$5\,\text{min} 14\,\text{s}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das Anbringen der Verzierungen kostet insgesamt ca. $6$ Minuten und $14$ Sekunden Zeit.

1.4.1

$\blacktriangleright$ Erwartungswert und Standardabweichung berechnen

Führe hier eine Zufallsvariable $X$ ein, die die Anzahl der kaputten Gläser in einer Tagesproduktion beschreibt. Bestimme deren Verteilung und berechne anschließend mit den passenden Formeln den Erwartungswert und die Standardabweichung.

Die Zufallsvariable $X$ kann als binomialverteilt mit den Parametern $n= 2.000$ und $p= 0,015$ angenommen werden, da bei jedem Glas nur zwei Möglichkeiten unterschieden werden („fehlerhaft“ und „fehlerfrei“) und die Wahrscheinlichkeit bei jedem Glas gleich hoch ist, dass es fehlerhaft ist.

Bei einer binomialverteilten Zufallsvariable mit den Parametern $n$ und $p$ kannst du den Erwartungswert $\mu$ und die Standardabweichung $\sigma$ mit folgenden Formeln berechnen:

$\mu = n\cdot p$ $\sigma = \sqrt{n\cdot p \cdot (1-p)}$

$\mu = 2.000 \cdot 0,015 = 30$

$\sigma\approx 5,44$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Erwartungswert der zufälligen Anzahl fehlerhafter Gläser in einer Tagesproduktion beträgt $30$ , die Standardabweichung ist ca. $5,44$ .

1.4.2

$\blacktriangleright$ Höchstzahl fehlerhafter Gläser ermitteln

Gesucht ist die höchste Anzahl $k$ an fehlerhaften Gläsern, die in einer Tagesproduktion gefunden werden können, sodass man gerade noch davon ausgehen kann, dass sich die Fehlerquote nicht erhöht hat. Dabei soll eine Irrtumswahrscheinlichkeit von $5\,\%$ nicht überschritten werden.

Diese Irrtumswahrscheinlichkeit $\alpha$ gibt an, dass die Wahrscheinlichkeit dafür, dass mehr als $k$ fehlerhafte Gläser gefunden werden, obwohl eigentlich die ursprüngliche Wahrscheinlichkeit von $1,5\,\%$ gilt, höchstens $5\,\%$ betragen soll.

Betrachtest du also die Zufallsvariable $X$ aus dem vorherigen Aufgabenteil, dann kannst du diese Bedingung wie folgt formulieren:

Es muss gelten: $P(X \gt k) \leq 0,05$

Gesucht ist nun das kleinste $k$ , das diese Ungleichung gerade noch erfüllt.

Bringe diesen Ausdruck zunächst in die Form $P(X \leq k)$ , um die kumulierte Binomialverteilung verwenden zu können.

$P(X \leq k)\geq 0,95$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das kleinste passende $k$ kannst du mit deinem CAS bestimmen, indem du dir dort eine Tabelle mit den kumulierten Werten der Binomialverteilung anzeigen lässt. Gehe dazu in das Tabellen-Menü und gib in die erste Spalte eine Folge für $k$ ein, also alle Zahlen von $0$ bis $2.000$ . Diese kannst du wie folgt einfügen:

menu $\to$ 3: Daten $\to$ 1: Folge erzeugen

Dialogfenster zur Eingabe einer mathematischen Folge mit verschiedenen Parametern.

Abb. 2: Folge erzeugen

In die zweite Spalte trägst du dann den Befehl für die kumulierte Binomialverteilung in Abhängigkeit der ersten Spalte ein:

binomCdf(2.000, 0,015, a)

In der Zeile mit $k =3$ steht nun beispielsweise die Wahrscheinlichkeit $P(X \le 3)$ .

Tabelle mit Berechnungen und Formeln in einer Softwareanwendung.

Abb. 3: Binomialtabelle

Wähle nun aus der Liste das kleinste $k$ , bei dem gerade noch $P(X \leq k) \geq 0,05$ ist. Es ist $P(X\leq 38) \approx 0,94 \leq 0,95$ und $P(X \leq 39) \approx 0,96 \geq 0,95$ . $k =39$ ist also die gesuchte Grenze.

Tabelle mit Berechnungen und Ergebnissen für eine statistische Analyse.

Abb. 4: Parameterauswahl

Werden also mehr als $39$ fehlerhafte Gläser in der Tagesproduktion gefunden, muss man mit einer Irrtumswahrscheinlichkeit von $5\,\%$ davon ausgehen, dass sich die Fehlerquote erhöht hat. Bei höchstens $39$ fehlerhaften Gläsern kann man dagegen bei der genannten Irrtumswahrscheinlichkeit noch davon ausgehen, dass sich die Fehlerquote nicht erhöht hat.

Bildnachweise [nach oben]

[1]

© 2017 - SchulLV.

[2]

© 2017 - SchulLV.

[3]

© 2017 - SchulLV.

[4]

© 2017 - SchulLV.

B1 Analysis und Stochastik

1.1

$\blacktriangleright$ Innendurchmesser ermitteln

Gesucht ist der Innendurchmesser des Glases in einer Höhe von $6\,\text{cm}$ . Der Verlauf der Innenwand wird durch die Funktion $f$ beschrieben. Die Höhe wird vom Boden aus gemessen, der durch die Gerade $x_1 = -1$ modelliert wird. Die Höhe des Glases von $6\,\text{cm}$ befindet sich also an der Stelle $x = 6-1 = 5$ . Berechne also $f(5)$ :

$f(5) = 1,3\cdot \sqrt{5}$

Da der Durchmesser gesucht ist, musst du den Radius noch verdoppeln:

$2\cdot 1,3\cdot \sqrt{5} \approx 5,81\,\text{[cm]}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

In einer Höhe von $6\,\text{cm}$ besitzt das Glas einen Innendurchmesser von ca. $5,81\,\text{cm}$ .

$\blacktriangleright$ Höhe des Glases berechnen

Für die Dicke des Randes gilt $d(x)= a(x)- f(x)$ . Berechne den Wert für $x$ für welchen $d(x)=0,2$ ist:

$x=9,94~\text{cm}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Auch hier musst du wieder $1~\text{cm}$ dazurechnen, da der Boden bei $x=-1$ anfängt.
Somit ist das Glas $10,94 \,\text{cm}$ hoch.

$\blacktriangleright$ Verlauf der Glaswand nachweisen

Du sollst nachweisen, dass die Dicke der Glaswand von unten nach oben hin immer geringer wird. Die Dicke wird für $x \gt 0$ parallel zum Boden gemessen. Sie wird durch den Abstand zwischen den beiden Funktionsgraphen $a$ und $f$ modelliert. Den Abstand an der Stelle $x$ kannst du mit der Differenz $d$ der beiden Funktionen beschreiben. Der Abstand wird immer geringer, wenn der Graph von $d$ streng monoton fallend ist. Dies kannst du mit Hilfe der ersten Ableitung $d‘$ überprüfen. Ist diese kleiner als Null für alle $x \gt 0$ , dann ist der Graph von $d$ streng monoton fallend.

$\begin{array}[t]{rll} d(x)&=& -0,001x^3... \\[10pt] d‘(x)&=&-0,003x^2... \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Überprüfe nun, für welche $x$ $d‘(x) \lt 0$ gilt. Dazu kannst du den solve-Befehl deines CAS verwenden.

Du erhältst folgende Lösung:

$x \gt 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für alle $x \gt 0$ ist also $d‘(x) \lt 0$ , also ist die Differenz der beiden Funktionen $a$ und $f$ streng monoton fallend. Da diese die Dicke der Glaswand beschreibt, nimmt die Dicke von unten nach oben betrachtet immer weiter ab.

1.2

$\blacktriangleright$ Füllhöhe ermitteln

Du sollst ermitteln, wie weit die Flüssigkeit unterhalb des Rands steht. Das Glas ist zu zwei Dritteln des Gesamtvolumens gefüllt. Der Teil des Glases, der gefüllt werden kann, wird durch die Innenwand begrenzt. Das Gesamtvolumen ergibt sich also als Rotationsvolumen des Graphen von $f$ .
Du kannst also wie folgt vorgehen:

Berechne das Gesamtvolumen an Flüssigkeit, die in das Glas passt, mit Hilfe eines Rotationsvolumens. Das Volumen der eingefüllten Flüssigkeit beträgt zwei Drittel des Gesamtvolumens.
Setze das Volumen der eingefüllten Flüssigkeit in die Formel für das Rotationsvolumen ein. Die Gleichung kannst du dann nach der oberen Grenze lösen und erhältst so den Füllstand des Glases.

1. Schritt: Volumen der Flüssigkeit berechnen

Das Innere des Glases kann durch einen Rotationskörper des Graphen von $f$ um die $x$ -Achse dargestellt werden. Ein solches Rotationsvolumen kannst du mit folgender Formel berechnen:

$V_x = \pi \cdot \displaystyle\int_{a}^{b}\left( f(x)\right)^2 \;\mathrm dx$

Für die untere Grenze musst du $a=0$ einsetzen, da der innere Rand des Glases bei $x=0$ beginnt.
Das Glas ist $11\,\text{cm}$ hoch. Die Höhe wird aber vom Boden an gemessen, der durch die Gerade $x_1 = -1$ beschrieben wird. Der obere Rand des Glases befindet sich daher an der Stelle $b = 10$ .

Das Integral kannst du mit deinem CAS berechnen. Den Befehl dafür findest du wie folgt:

keyboard $\to$ Math2

$V_{\text{Gesamt}} = \pi \cdot 84,5 \,\text{[VE]}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das Volumen der eingefüllten Flüssigkeit ist also $V_{\text{Flüssigkeit}} = \frac{169}{3}\cdot \pi$

2. Schritt: Gleichsetzen

Gesucht ist nun die obere Grenze $b$ des Rotationsvolumens mit $V_{\text{Flüssigkeit}} = \frac{169}{3}\cdot \pi$ .

$\begin{array}[t]{rll} \pi \cdot \displaystyle\int_{0}^{b}\left( f(x)\right)^2 \;\mathrm dx &=& ... \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Löse diese Gleichung mit dem solve-Befehl deines CAS nach $b$ . Du erhältst dann die Lösungen $b_1 \approx 8,16$ und $b_2\approx -8,16$ , wobei $b_2$ wegfällt, da nur der Bereich $x \gt 0$ betrachtet wird.

Da sich der Rand bei $x =10$ befindet, ist die Flüssigkeit also bis ca. $1,84\,\text{cm}$ unterhalb des Randes gefüllt.

$\blacktriangleright$ Größe des evakuierten Raumes berechnen

Der Raum, der evakuiert werden soll, entsteht aus dem Rotationskörper des Graphen von $a$ um die $x$ -Achse im Bereich $a_1 = -1$ und $b = 10$ , aus dem der Rotationskörper des Graphen von $f$ im Bereich $a_2 = 0$ und $b$ herausgelöst wird.

Das Volumen des inneren Teils hast du bereits berechnet. Das Volumen des äußeren Teils kannst du mit der gleichen Formel berechnen.

$V_{\text{außen}} \approx 396,41$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das Volumen des evakuierten Raumes ergibt sich damit wie folgt:

$V_{\text{Evakuiert}} \approx 130,96$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der evakuierte Raum hat eine Größe von ca. $130,96\,\text{cm}^2$ .

1.3

$\blacktriangleright$ Zeit zum Anbringen der Verzierungen berechnen

Um die Zeit zu berechnen, die für alle Verzierungen benötigt wird, musst du die Gesamtlänge aller Verzierungen berechnen. Diese setzt sich zusammen aus zwei Arten von Schliffen:

Der Schliff rund um das Glas:
Die Länge ist der Umfang eines Kreises, dessen Radius der Funktionswert von $a$ an der entsprechenden Stelle ist.
Die drei Schliffe senkrecht zum Boden: Diese Schliffe verlaufen entlang der Außenwand. Sie besitzen die gleiche Länge, die über die Bogenlänge des Graphen von $a$ im entsprechenden Intervall berechnet werden kann. Dazu kann folgende Formel verwendet werden:

$s = \displaystyle\int_{a}^{b}\sqrt{1+ \left[f‘(x)\right]^2}\;\mathrm dx$

1. Schritt: Länge des ersten Schliffs berechnen

Da die Höhe des Glases vom Boden aus gemessen wird und dieser bei $x_1 = -1$ liegt, kannst du den Radius des Glases in der Höhe $8,5\,\text{cm}$ über $a(7,5)$ berechnen.

$a(7,5) \approx 4,09$

Damit kannst du nun den Umfang des Glases berechnen:

$\begin{array}[t]{rll} U&=&2\cdot \pi \cdot r \\[5pt] &=& 2\cdot \pi \cdot a(7,5) \\[5pt] &\approx& 2\cdot \pi \cdot 4,09 \,\text{cm}\\[5pt] &\approx& 25,70 \,\text{cm} \end{array}$

Der erste Schliff ist ca. $25,70\,\text{cm}$ lang.

2. Schritt: Länge der senkrechten Schliffe berechnen

Die Länge der senkrechten Schliffe kannst du über die Bogenlänge des Graphen von $a$ berechnen. Die Schliffe laufen senkrecht vom ersten Schliff nach unten zum Boden. Du benötigst also die Bogenlänge von $a = -1$ bis $b = 7,5$ .
Das Integral kannst du wieder mit deinem CAS berechnen:

$s \approx 8,86$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einer der drei senkrechten Schliffe ist also ca. $8,86\,\text{cm}$ lang.

Insgesamt ergibt sich also folgende Gesamtlänge aller Schliffe:

$S = 52,28\,\text{cm}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

3. Schritt: Benötigte Zeit berechnen

Für $1\,\text{cm}$ werden ca. $6$ Sekunden benötigt. Die Schliffe haben insgesamt eine Länge von ca. $52,28\,\text{cm}$ . Es ergibt sich dann folgende Zeit:

$5\,\text{min} 14\,\text{s}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das Anbringen der Verzierungen kostet insgesamt ca. $6$ Minuten und $14$ Sekunden Zeit.

1.4.1

$\blacktriangleright$ Erwartungswert und Standardabweichung berechnen

Führe hier eine Zufallsvariable $X$ ein, die die Anzahl der kaputten Gläser in einer Tagesproduktion beschreibt. Bestimme deren Verteilung und berechne anschließend mit den passenden Formeln den Erwartungswert und die Standardabweichung.

Die Zufallsvariable $X$ kann als binomialverteilt mit den Parametern $n= 2.000$ und $p= 0,015$ angenommen werden, da bei jedem Glas nur zwei Möglichkeiten unterschieden werden („fehlerhaft“ und „fehlerfrei“) und die Wahrscheinlichkeit bei jedem Glas gleich hoch ist, dass es fehlerhaft ist.

Bei einer binomialverteilten Zufallsvariable mit den Parametern $n$ und $p$ kannst du den Erwartungswert $\mu$ und die Standardabweichung $\sigma$ mit folgenden Formeln berechnen:

$\mu = n\cdot p$ $\sigma = \sqrt{n\cdot p \cdot (1-p)}$

$\mu = 2.000 \cdot 0,015 = 30$

$\sigma\approx 5,44$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Erwartungswert der zufälligen Anzahl fehlerhafter Gläser in einer Tagesproduktion beträgt $30$ , die Standardabweichung ist ca. $5,44$ .

1.4.2

$\blacktriangleright$ Höchstzahl fehlerhafter Gläser ermitteln

Gesucht ist die höchste Anzahl $k$ an fehlerhaften Gläsern, die in einer Tagesproduktion gefunden werden können, sodass man gerade noch davon ausgehen kann, dass sich die Fehlerquote nicht erhöht hat. Dabei soll eine Irrtumswahrscheinlichkeit von $5\,\%$ nicht überschritten werden.

Diese Irrtumswahrscheinlichkeit $\alpha$ gibt an, dass die Wahrscheinlichkeit dafür, dass mehr als $k$ fehlerhafte Gläser gefunden werden, obwohl eigentlich die ursprüngliche Wahrscheinlichkeit von $1,5\,\%$ gilt, höchstens $5\,\%$ betragen soll.

Betrachtest du also die Zufallsvariable $X$ aus dem vorherigen Aufgabenteil, dann kannst du diese Bedingung wie folgt formulieren:

Es muss gelten: $P(X \gt k) \leq 0,05$

Gesucht ist nun das kleinste $k$ , das diese Ungleichung gerade noch erfüllt.

Bringe diesen Ausdruck zunächst in die Form $P(X \leq k)$ , um die kumulierte Binomialverteilung verwenden zu können.

$P(X \leq k)\geq 0,95$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Dafür benötigst du den Befehl für die inverse Binomialverteilung. Diesen kannst du im Statistik-Menü wie folgt finden:

Calc $\to$ Inv. Verteilung $\to$ Inv. Binomial-Verteilung

Gib dort die Parameter ein. Du erhältst folgendes Ergebnis:

$k =39$ .

Eingabefelder für eine statistische Berechnung mit Schaltflächen für Navigation und Hilfe.

Abb. 1: Parameter eingeben

Für $k =39$ ist also $P(X \leq 39) \approx 0,95$ . Da dieser Wert gerundet ist, kann es sein, dass die Wahrscheinlichkeit entweder knapp über oder knapp unter $0,95$ liegt. Du musst also noch überprüfen, ob $P(X \leq 39) \geq 0,95$ ist. Diese Wahrscheinlichkeit kannst du im gleichen Menü mit der Binom. Vert.-Funktion bestimmen und erhältst:

$P(X\leq 39)\approx0,955 \gt 0,95$

Eingabemaske mit numerischen Werten und Schaltflächen für Rückkehr und Hilfe.

Abb. 2: Ergebnis

Werden also mehr als $39$ fehlerhafte Gläser in der Tagesproduktion gefunden, muss man mit einer Irrtumswahrscheinlichkeit von $5\,\%$ davon ausgehen, dass sich die Fehlerquote erhöht hat. Bei höchstens $39$ fehlerhaften Gläsern kann man dagegen bei der genannten Irrtumswahrscheinlichkeit noch davon ausgehen, dass sich die Fehlerquote nicht erhöht hat.

Bildnachweise [nach oben]

[1]

© 2017 - SchulLV.

[2]

© 2017 - SchulLV.