Stochastik
Das jährlich stattfindende regionale Sportevent „Brückenlauf“ erfreut sich zunehmender Beliebtheit und steigender Teilnehmerzahlen. Die folgende Tabelle zeigt für den „12. Brückenlauf“, an dem insgesamt 4650 Personen teilnahmen, die Verteilung der Teilnehmer auf die einzelnen Kategorien sowie für jede Kategorie den Anteil weiblicher Teilnehmer. Jeder Teilnehmer entscheidet sich für genau eine Kategorie. Beim Marathon gibt es die Wahl zwischen Halb- und Vollmarathon.
 Beurteile die folgenden Aussagen eines Reporters über die Teilnehmer am „12. Brückenlauf“:
I „Beim diesjährigen ‚Brückenlauf‘ waren deutlich weniger männliche als weibliche Starter dabei.“
II „Etwa ein Sechstel der nicht weiblichen Teilnehmer waren Walker.“
Beurteile die folgenden Aussagen eines Reporters über die Teilnehmer am „12. Brückenlauf“:
I „Beim diesjährigen ‚Brückenlauf‘ waren deutlich weniger männliche als weibliche Starter dabei.“
II „Etwa ein Sechstel der nicht weiblichen Teilnehmer waren Walker.“
| Kategorie | Anteil an allen Startern | Anteil weiblicher Teilnehmer je Kategorie |
|---|---|---|
| 6 km Walking | 23,0 % | 78,4 % |
| 12 km Walking | 9,8 % | 72,7 % |
| 6 km Lauf | 22,8 % | 51,4 % |
| 12 km Lauf | 25,3 % | 38,5 % |
| 21 km Halb-Marathon | 15,4 % | 32,3 % |
| 42 km Voll-Marathon | 3,7 % | 18,7 % |
3.1
Berechne die Gesamtanzahl der Teilnehmer an den Marathonläufen beim „12. Brückenlauf“.
(2 BE)
3.2
Es wird zufällig eine Person ausgewählt, die am „Brückenlauf“ teilgenommen hat.
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
(A) Die Person ist kein Marathonteilnehmer.
(B) Die Person ist ein weiblicher Marathonteilnehmer.
(3 BE)
3.3
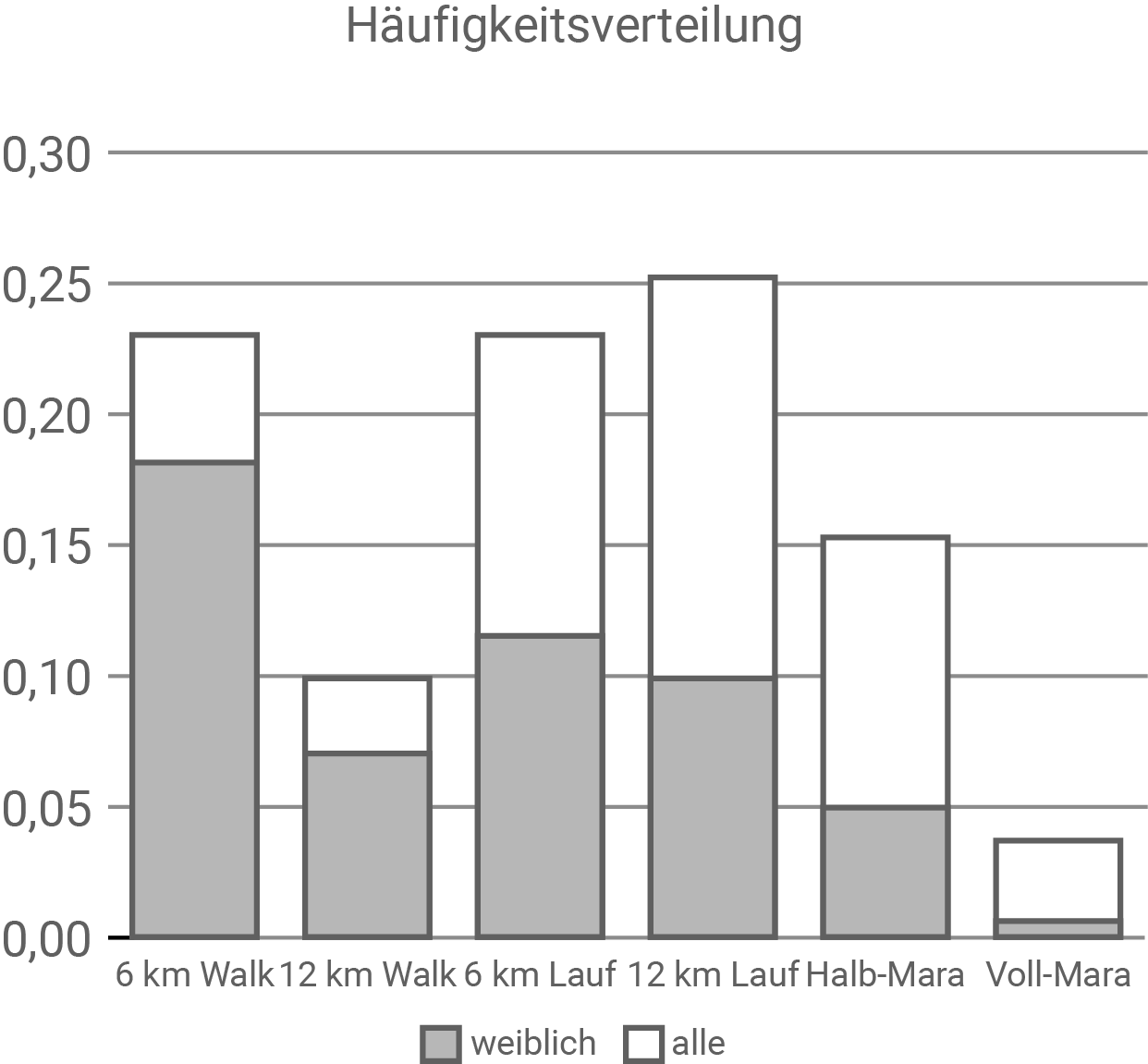
Stelle die Häufigkeitsverteilung der Teilnehmer an den möglichen Laufstreckenlängen in einem Säulendiagramm dar. Markiere in dem Diagramm den jeweiligen Anteil weiblicher bzw. nicht weiblicher Teilnehmer.
(5 BE)
3.4
Das unbeschriftete Baumdiagramm erfasst für einen zufällig ausgewählten Teilnehmer die Merkmale „Geschlecht“ ( = weiblich,
= weiblich,  = nicht weiblich) und „Startkategorie“ (
= nicht weiblich) und „Startkategorie“ ( = Teilnahme am Walking,
= Teilnahme am Walking,  = keine Teilnahme am Walking).
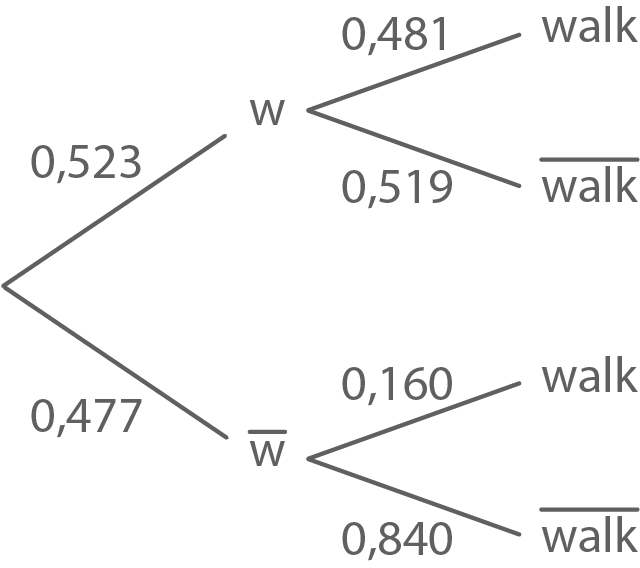
Übernimm die nebenstehende Abbildung.
Ermittle und ergänze die Wahrscheinlichkeiten der Teilpfade.
= keine Teilnahme am Walking).
Übernimm die nebenstehende Abbildung.
Ermittle und ergänze die Wahrscheinlichkeiten der Teilpfade.

(7 BE)
3.5
Zum „Brückenlauf“ meldet sich eine Familie mit 9 Personen an.
Gib ein Argument dafür an, dass die Verteilung der Familienmitglieder auf die einzelnen Kategorien nicht der Häufigkeitsverteilung aus der Tabelle entspricht.
(1 BE)
3.6
Durch eine breit angelegte Werbekampagne streben die Organisatoren an, die Anzahl der Teilnehmer am „Brückenlauf“ im Jahr 2022 auf etwa 5500 zu steigern. In Vorbereitung des Brückenlaufes gehen sie modellhaft davon aus, dass diese Teilnehmerzahl genau erreicht wird und jeder Teilnehmer mit einer Wahrscheinlichkeit in eine Kategorie fällt, die der Häufigkeit dieser Kategorie beim „12. Brückenlauf“ entspricht.
3.6.1
In diesem Modell entspricht die Zufallsgröße  der Anzahl an Teilnehmern in der Kategorie Voll-Marathon im Jahr 2022.
Berechne die Wahrscheinlichkeit dafür, dass der Wert dieser Zufallsgröße ihren Erwartungswert um mehr als eine Standardabweichung übersteigt.
der Anzahl an Teilnehmern in der Kategorie Voll-Marathon im Jahr 2022.
Berechne die Wahrscheinlichkeit dafür, dass der Wert dieser Zufallsgröße ihren Erwartungswert um mehr als eine Standardabweichung übersteigt.
(4 BE)
3.6.2
Für die Teilnahme am „Brückenlauf“ muss eine Startgebühr entrichtet werden. Teilnehmer am Marathon zahlen 25 €, alle anderen 15 € Startgebühren. Erfolgt eine Anmeldung verspätet, d. h. erst am Vortag oder am Morgen des „Brückenlaufs“, muss eine Nachmeldegebühr in Höhe von 5 € entrichtet werden, erfahrungsgemäß betrifft dies 8 % aller Teilnehmer.
Berechne die für 2022 zu erwartenden Einnahmen aus den Startgebühren.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
Es sind die Anzahl der Teilnehmer in den Kategorien „Halbmarathon“ und „Vollmarathon" zu berechnen:

 Es sind ca. 888 Teilnehmer.
Es sind ca. 888 Teilnehmer.
3.2
3.3
3.4
Aussage I ist falsch, da etwa  der Teilnehmer weiblich sind und das Verhältnis zwischen weiblich und nicht weiblich somit annähernd ausgeglichen ist.
Aussage II ist korrekt, da der Anteil der männlichen Walker etwa
der Teilnehmer weiblich sind und das Verhältnis zwischen weiblich und nicht weiblich somit annähernd ausgeglichen ist.
Aussage II ist korrekt, da der Anteil der männlichen Walker etwa  beträgt, was annährend dem Wert
beträgt, was annährend dem Wert  entspricht.
entspricht.
3.5
Interessen können familiär geprägt sein, sodass häufig Familienmitglieder gemeinsam in einer Kategorie starten.
3.6.1
X entspricht der Anzahl an Teilnehmern in der Kategorie Voll-Marathon,  kann als binomialverteilt betrachtet werden:
kann als binomialverteilt betrachtet werden:









 Die Wahrscheinlichkeit beträgt etwa
Die Wahrscheinlichkeit beträgt etwa  .
.
3.6.2