Wahlpflichtaufgaben (Aufgabengruppe 2)

5.1

Gegeben sind die Funktion $f$ mit $f(x)=\sqrt{x}$ und $x \in \mathbb{R}, x \geq 0$ , und die Gerade $g$ mit der Gleichung $y=\dfrac{1}{4} x.$

Betrachtet wird das Intervall, das von den $x$ -Koordinaten der beiden Schnittpunkte des Graphen von $f$ und der Gerade $g$ begrenzt wird. In diesem Intervall gibt es eine Stelle, an der die lokale Änderungsrate von $f$ mit der mittleren Änderungsrate von $f$ in diesem Intervall übereinstimmt.

Bestimme diese Stelle.

(5 BE)

5.2

Betrachtet wird das Quadrat, das die folgenden Eigenschaften besitzt:

Das Quadrat liegt in der $xy$ -Ebene.
Ein Eckpunkt liegt im Koordinatenursprung.
Der Schnittpunkt der Diagonalen des Quadrats liegt auf der Gerade $g: \overrightarrow{x}=\pmatrix{-1\\4\\-2}+\lambda\cdot \pmatrix{2\\0\\1}$ mit $\lambda \in\mathbb{R}.$

Bestimme die Koordinaten des Schnittpunkts der Diagonalen und berechne den Flächeninhalt des Quadrats.

(5 BE)

5.3

In einem Betrieb werden Geräte hergestellt, von denen jedes mit einer Wahrscheinlichkeit von $90 \,\%$ fehlerfrei ist.

Bevor ein Gerät in den Verkauf gehen kann, wird es einer Endkontrolle unterzogen. Dabei identifiziert die Endkontrolle ein fehlerfreies Gerät mit einer Wahrscheinlichkeit von $99 \,\%.$ Dagegen wird ein fehlerhaftes Gerät mit einer Wahrscheinlichkeit von $5 \,\%$ ebenfalls als fehlerfrei eingestuft.

Zeige, dass die Wahrscheinlichkeit dafür, dass ein Gerät fehlerfrei ist und als fehlerfrei eingestuft wird, $89,1 \,\%$ beträgt.

(2 BE)

Formuliere eine Aussage im Sachzusammenhang, die sich in Verbindung mit der Gleichung $0,891+0,1 \cdot 0,05=0,896$ aus der Ungleichung $\displaystyle\sum\limits_{k=90}^{100} \pmatrix{100\\k}\cdot 0,896^k\cdot 0,104^{100-k}\gt 0,5$ ergibt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

5.1

1. Schritt: Schnittpunkte bestimmen

$\begin{array}[t]{rll} \sqrt{x}&=& \dfrac{1}{4}x&\quad \scriptsize \mid\;(\,)^2 \\[5pt] x&=& \dfrac{1}{16}x^2&\quad \scriptsize \mid\; -x \\[5pt] 0&=& \dfrac{1}{16}x^2 -x & \\[5pt] 0&=& x\cdot \left(\dfrac{1}{16}x-1\right) & \\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgen die Schnittstellen direkt mit $x_1=0$ und:

$\begin{array}[t]{rll} 0&=& \dfrac{1}{16}x-1&\quad \scriptsize \mid\; +1\\[5pt] 1&=& \dfrac{1}{16}x&\quad \scriptsize \mid\; \cdot 16\\[5pt] 16&=& x_2 \end{array}$

2. Schritt: Mittlere Änderungsrate bestimmen

$\begin{array}[t]{rll} \dfrac{f(16)-f(0)}{16-0}&=& \dfrac{\sqrt{16}-\sqrt{0}}{16-0}& \\[5pt] &=& \dfrac{4-0}{16}&\\[5pt] &=& \dfrac{1}{4} \end{array}$

3. Schritt: Lokale Änderungsrate ermitteln

Erste Ableitungsfunktion berechnen:

$\(f$

Gesucht ist die Stelle im Intervall $[0;16],$ an der gilt:

$\(\begin{array}[t]{rll} f$

Die Stelle, an der die lokale Änderungsrate von $f$ mit der mittleren Änderungsrate von $f$ übereinstimmt, ist somit gegeben durch $x=4.$

5.2

Schnittpunkt bestimmen

Da das Quadrat in der $xy$ -Ebene liegt, gilt für den Schnittpunkt der Diagonalen:

$\pmatrix{x\\y\\0}= \pmatrix{-1\\4\\-2}+\lambda\cdot \pmatrix{2\\0\\1}$

Aus der dritten Zeile folgt also:

$\begin{array}[t]{rll} -2+\lambda \cdot 1&=& 0 &\quad \scriptsize \mid\; +2 \\[5pt] \lambda&=& 2 \end{array}$

Einsetzen in die Geradengleichung liefert:

$\begin{array}[t]{rll} \overrightarrow{OS}&=& \pmatrix{-1\\4\\-2}+2\cdot \pmatrix{2\\0\\1}& \\[5pt] &=& \pmatrix{3\\4\\0} \end{array}$

Der Schnittpunkt der Diagonalen hat also die Koordinaten $S(3\mid 4\mid 0).$

Flächeninhalt berechnen

Da der Schnittpunkt $S$ der Diagonalen genau in der Mitte des Quadrats liegt und ein Eckpunkt des Quadrats mit den Koordinaten $A(0\mid 0\mid 0)$ gegeben ist, folgt für die Koordinaten des gegenüberliegenden Eckpunkts $C:$

$\begin{array}[t]{rll} \overrightarrow{OC}&=& \overrightarrow{OA}+2\cdot \overrightarrow{AS}&\\[5pt] &=& \pmatrix{0\\0\\0}+2\cdot \pmatrix{3\\4\\0} &\\[5pt] &=& \pmatrix{6\\8\\0} \end{array}$

Hilfsskizze

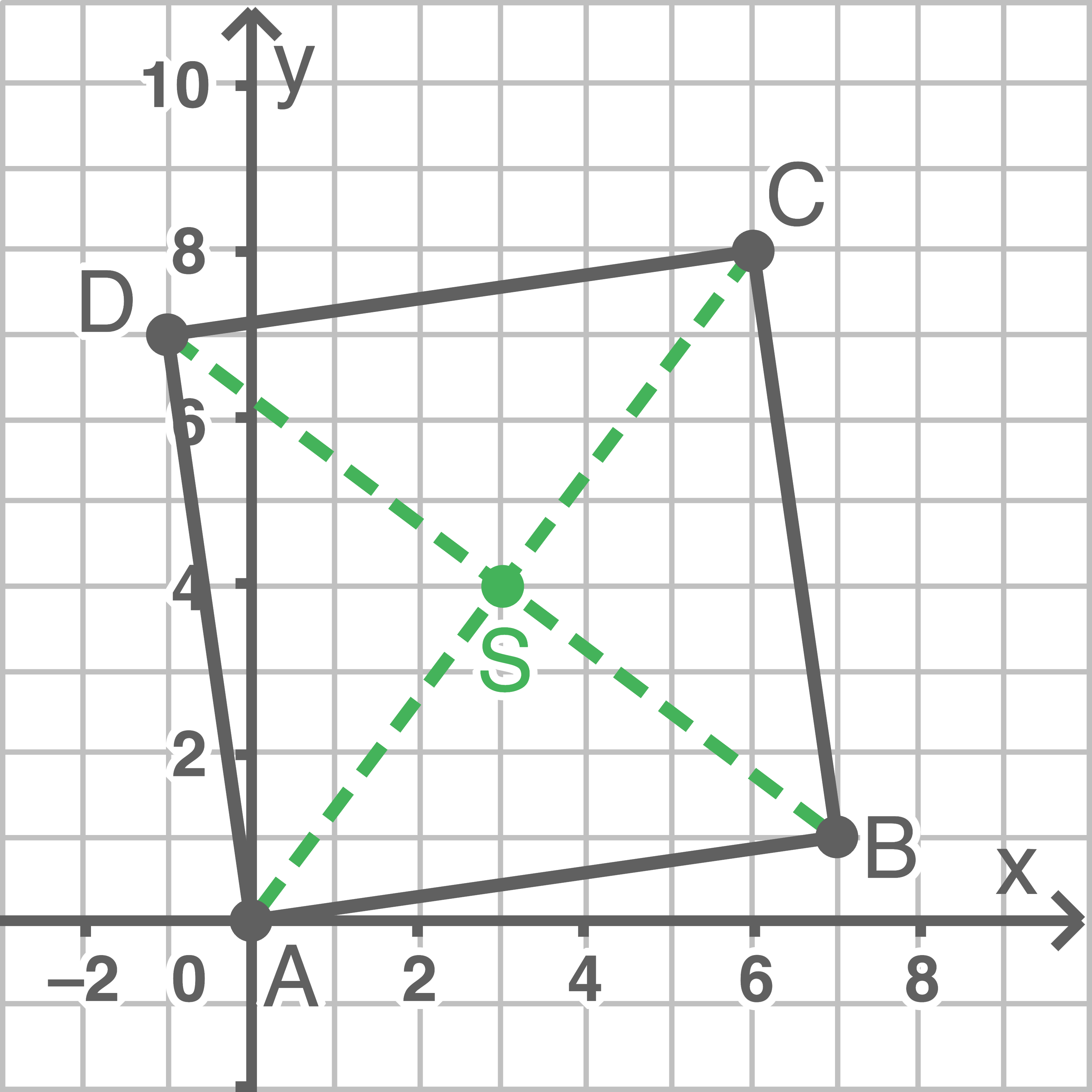Die Länge $d$ der Diagonalen ergibt sich also zu:

$\begin{array}[t]{rll} d&=& \left| \overrightarrow{AC} \right|&\\[5pt] &=& \left| \pmatrix{6\\8\\0} \right|&\\[5pt] &=& \sqrt{6^2+8^2+0^2} &\\[5pt] &=& \sqrt{100} &\\[5pt] &=& 10 \end{array}$

Mit dem Satz des Pythagoras ergibt sich für die Seitenlänge $a$ des Quadrats:

$\begin{array}[t]{rll} a^2+a^2&=& d^2& \\[5pt] 2a^2&=& 10^2&\quad \scriptsize \mid\; \sqrt{\,}\\[5pt] \sqrt{2}a&=& 10&\quad \scriptsize \mid\; :\sqrt{2}\\[5pt] a&=& \dfrac{10}{\sqrt{2}} \end{array}$

Der Flächeninhalt des Quadrats ergibt sich also zu:

$\begin{array}[t]{rll} A&=& a\cdot a&\\[5pt] &=& \left(\dfrac{10}{\sqrt{2}} \right)^2&\\[5pt] &=& \dfrac{100}{2}&\\[5pt] &=& 50 \; [\text{FE}] \end{array}$

5.3

Aus der Aufgabenstellung folgt:

Wahrscheinlichkeit, dass ein Gerät fehlerfrei ist: $P (\text{fehlerfrei})=0,90$

Wahrscheinlichkeit, dass ein fehlerfreies Gerät als fehlerfrei eingestuft wird: $P (\text { erkannt } \mid \text { fehlerfrei }) =0,99$

$P(\text { fehlerfrei und erkannt })=0,891$

Rechenweg anzeigen

Die erste Gleichung beschreibt die Gesamtwahrscheinlichkeit, dass ein Gerät als fehlerfrei eingestuft wird, unabhängig davon, ob es tatsächlich fehlerfrei ist oder nicht.

Die Summenformel beschreibt somit die Wahrscheinlichkeit, dass in einer Stichprobe von 100 Geräten mindestens 90 Geräte als fehlerfrei erkannt werden.

„Da ein kleiner Anteil fehlerhafter Geräte ebenfalls als fehlerfrei eingestuft wird, ist es wahrscheinlicher, dass mindestens $90\,\%$ der Geräte aus der Stichprobe von 100 Geräten als fehlerfrei erkannt werden, als dass weniger als die erwarteten $90\,\%$ der Geräte als fehlerhaft eingestuft werden.“

Alternative Lösung:

"Mit einer Wahrscheinlichkeit von über $50\,\%$ werden in einer Stichprobe von 100 Geräten mindestens 90 Geräte als fehlerfrei erkannt werden, da ein kleiner Anteil fehlerhafter Geräte ebenfalls als fehlerfrei eingestuft wird."

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?