Pflichtaufgaben

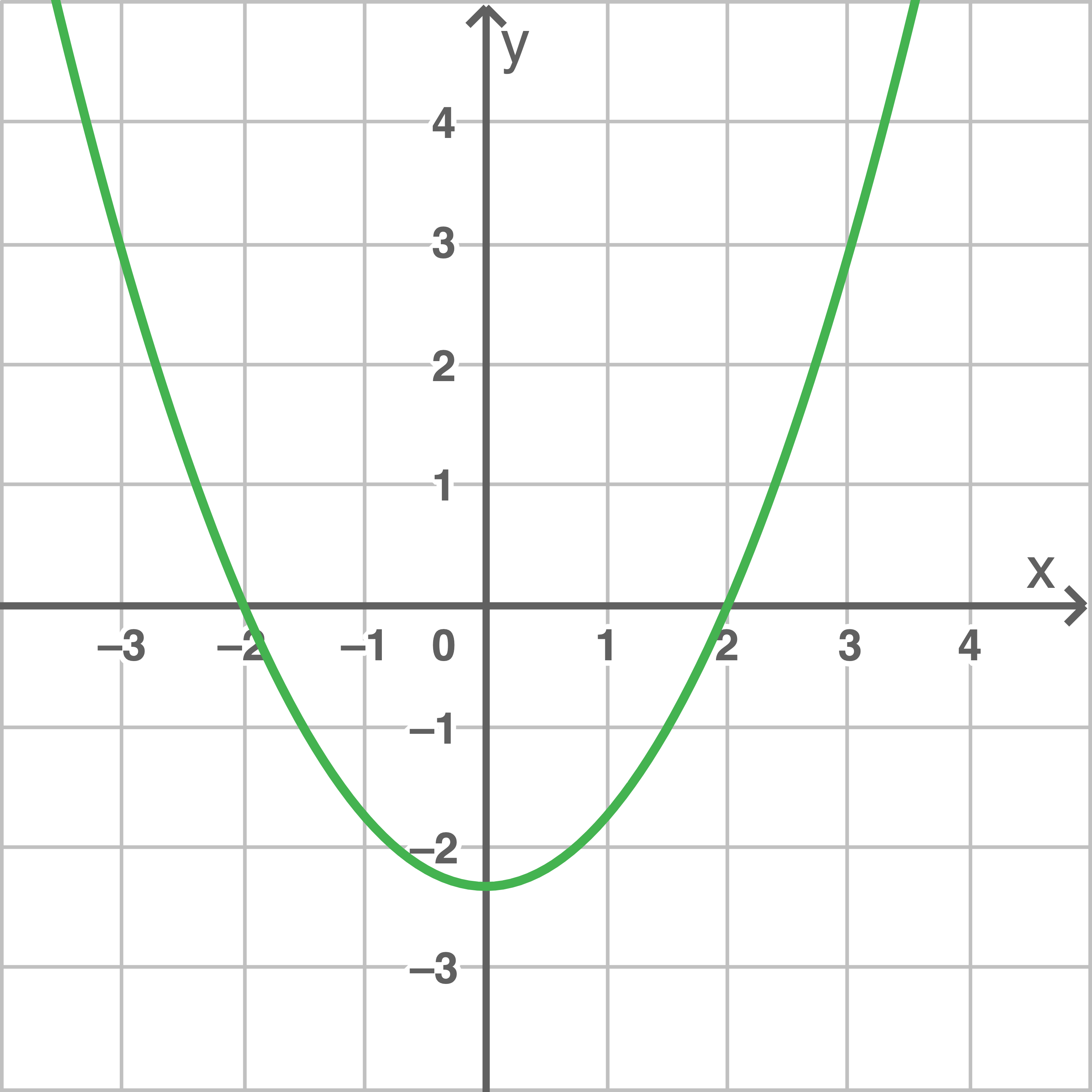
Die Abbildung zeigt den Graphen der Ableitungsfunktion $\(f$ einer in $\mathbb{R}$ definierten Funktion $f.$

Sachsen-Anhalt Abi 2022 grundlegendes Anforderungsniveau P1

Gib die Extremstellen der Funktion $f$ an.

(2 BE)

Begründe, dass für $0\lt x\lt 2$ gilt: $\(f$

(3 BE)

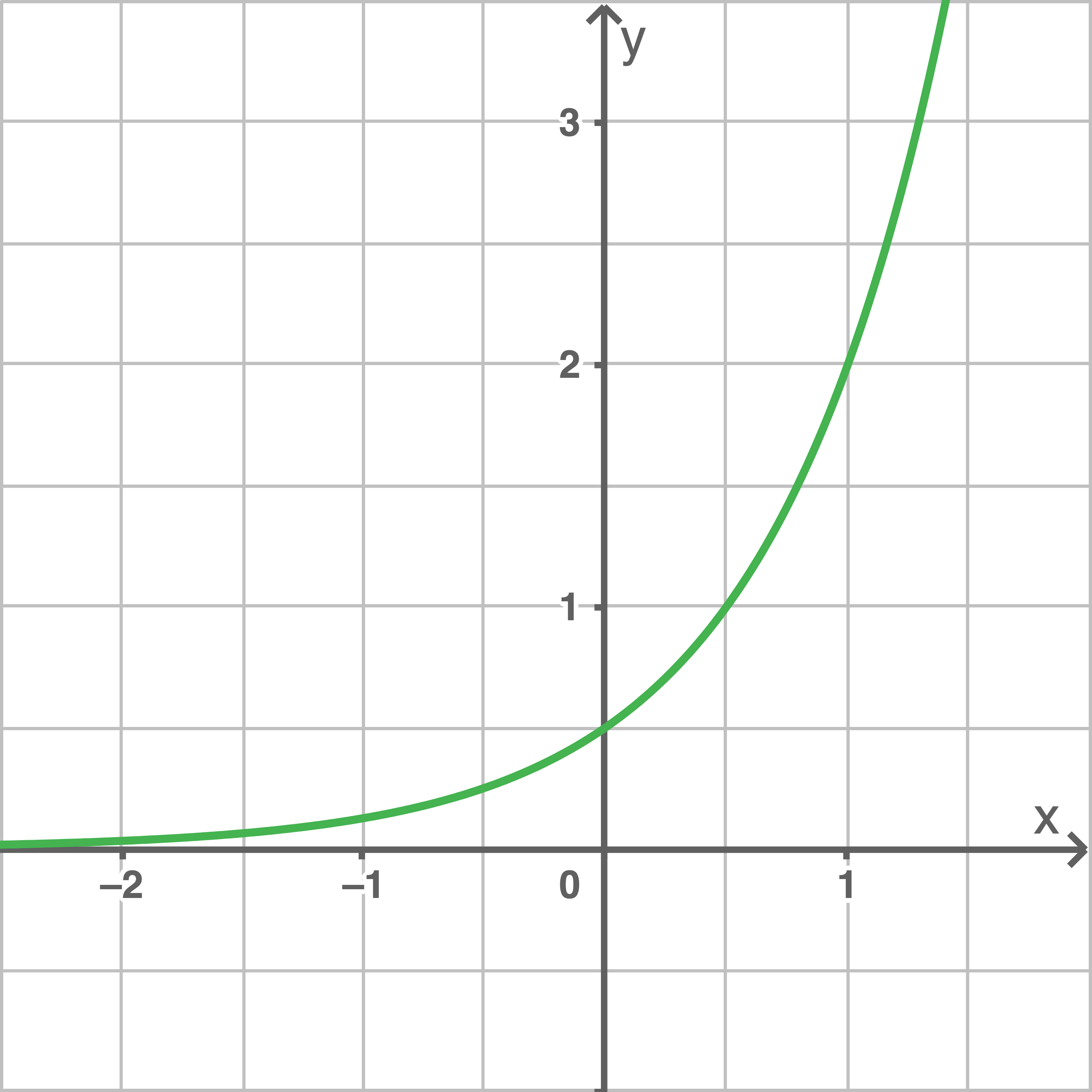
Die Abbildung zeigt den Graphen der Funktion $f$ mit $f(x)=a\cdot b^x$ mit $a, b \in \mathbb{R},$ $a\gt 0,\,b\gt 0.$

Bestimme die passenden Werte von $a$ und $b.$

Sachsen-Anhalt Abi 2022 grundlegendes Anforderungsniveau P2

(3 BE)

Der Graph der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=\mathrm{e}^x$ wird um 2 in negative $x$ -Richtung verschoben. Zeige, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von $g$ in $y$ -Richtung erzeugt werden kann.

(2 BE)

Gegeben sind die Punkte $P(2\mid 0\mid 1)$ und $Q(2\mid 4\mid 9)$ sowie die parallelen Geraden $g: \vec{x}=\overrightarrow{OP}+\lambda \cdot \pmatrix{3\\ -1\\2}$ und $h: \vec{x}=\overrightarrow{OQ}+\mu \cdot \pmatrix{3\\ -1\\2}$ mit $\lambda, \mu \in \mathbb{R}.$

Zeige, dass $g$ und $h$ nicht identisch sind.

(2 BE)

Bestimme eine Gleichung der Gerade, die parallel zu $g$ und $h$ ist und die Strecke $\overline{PQ}$ im Punkt $T$ schneidet, wobei $3 \cdot \left| \overline{PT}\right| =\left| \overline{QT}\right|$ gilt.

(3 BE)

$60 \,\%$ der Kunden eines Reiseunternehmens reisen gerne in die Region $A,$ $30 \,\%$ in die Region $B,$ $20 \,\%$ reisen in jede der beiden Regionen gerne.

Unter denjenigen Kunden, die gerne in die Region $A$ reisen, wird eine Person zufällig ausgewählt. Bestimme die Wahrscheinlichkeit dafür, dass diese Person auch gerne in die Region $B$ reist.

(2 BE)

Berechne den Anteil der Kunden, die entweder in die Region $A$ oder in die Region $B$ gerne reisen.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Extremstellen von $f$ sind Nullstellen von $\(f$ Aus der Abbildung lassen sich die Nullstellen ablesen. Die Extremstellen sind demnach bei $x_1=-2$ und $x_2=2.$

Der Graph von $\(f$ nimmt im Intervall $0\lt x\lt 2$ nur negative Funktionswerte an. Der Ableitungsgraph $\(f$ gibt die Steigung von $\(f$ an, diese ist im Intervall streng positiv. Somit ist das Produkt stets negativ.

Ablesen der Punkte $A(0\mid 0,5)$ und $B(1\mid 2).$

Koordinaten von $A$ in $f(x)$ eingesetzt: $0,5=a\cdot b^0,$ daraus folgt $a=0,5$ (da $b^0=1$ )

Koordinaten von $B$ sowie $a$ in $f(x)$ eingesetzt: $2=0,5\cdot b^1,$ daraus folgt $b=4$

$a=0,5;$ $b=4$

Verschiebung von $g(x):$

$g_2 = \mathrm{e}^\left(x+2 \right)$

Mit den Potenzregeln folgt:

$g_2 = \mathrm{e}^x \cdot \mathrm{e}^2$

Der Graph kann also auch durch eine Streckung in $y$ -Richtung um den Faktor $\mathrm{e}^2 \approx 7,39$ erzeugt werden.

Punktprobe von $P$ mit $h$ ergibt:

$\pmatrix{2\\0\\1}=\pmatrix{2\\4\\9}+\mu\pmatrix{3\\-1\\2}$

$\begin{array}{lrll} \text{I}\quad&2&=&2+3\mu\\ \text{II}\quad&0&=&4-\mu\\ \text{III}\quad&1&=&9+2\mu\\ \end{array}$

Aus $\text{II}$ folgt: $\mu=4$

$\mu=4$ in $\text{I}$ eingesetzt ergibt $2=2+3\cdot4,$ diese Gleichung ist nicht erfüllt.

Damit ist gezeigt, dass die Geraden nicht identisch sein können.

1. Schritt: Punkt $T$ bestimmen

$\overrightarrow{OT}=\overrightarrow{OP}+\dfrac{1}{4}\overrightarrow{PQ}$

$\overrightarrow{OT}=\pmatrix{2\\0\\1}+\dfrac{1}{4}\pmatrix{2-2\\4-0\\9-1}$ $=\pmatrix{2\\1\\3}$

2. Schritt: Richtungsvektor bestimmen und Geradengleichung aufstellen

Der Richtungsvektor der neuen Gerade $i$ entspricht einem Vielfachen der Richtungsvektoren der Geraden $g$ und $h.$

Somit gilt $i:\vec{x}=\pmatrix{2\\1\\3}+s\cdot \pmatrix{3\\-1\\2}.$

$\dfrac{0,2}{0,6}=\dfrac{1}{3}$

Der Anteil der Kunden, der gerne in beide Regionen reist, ist jeweils im Anteil der Kunden enthalten, der nur in eine der beiden Regionen gerne reist. Daher lässt sich der gesuchte Anteil wie folgt berechnen:

$0,6+0,3-2\cdot 0,2=0,5=50\,\%$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?