Aufgabe 3: Stochastik
Eine weltweit verbreitete Krankheit wird ausschließlich durch Infektion mit Bakterien verursacht. Ein Drittel aller Menschen infizieren sich im Laufe ihres Lebens mit den Bakterien. Bei 
derjenigen, die sich infizieren, bricht die Krankheit im Laufe ihres Lebens aus.
3.1
a)
Stelle den beschriebenen Sachzusammenhang in einem beschrifteten Baumdiagramm dar.
(3 BE)
b)
Ermittle den Anteil der Menschen, bei denen die Krankheit im Laufe ihres Lebens nicht ausbricht.
(2 BE)
c)
Bei einem zufällig ausgewählten Menschen bricht die Krankheit im Laufe seines Lebens nicht aus. Berechne die Wahrscheinlichkeit dafür, dass er sich im Laufe seines Lebens infiziert hat.
(3 BE)
3.2
Für zwei medizinische Studien zu der betrachteten Krankheit werden die Teilnehmerinnen und Teilnehmer zufällig ausgewählt. Die Anzahl der Infizierten unter den Teilnehmenden soll bei jeder der beiden Studien als binomialverteilt mit dem Parameter 
angenommen werden.
a)
Bei der ersten Studie beträgt der Erwartungswert für die Anzahl der Infizierten unter den Teilnehmenden 
Berechne die Anzahl der Teilnehmenden sowie die Wahrscheinlichkeit dafür, dass davon genau 
infiziert sind.
(2 BE)
b)
Bei der zweiten Studie ist die Wahrscheinlichkeit dafür, dass von den Teilnehmenden genau 
infiziert sind, etwa 
Bestimme eine mögliche Anzahl der Teilnehmenden.
(3 BE)
3.3
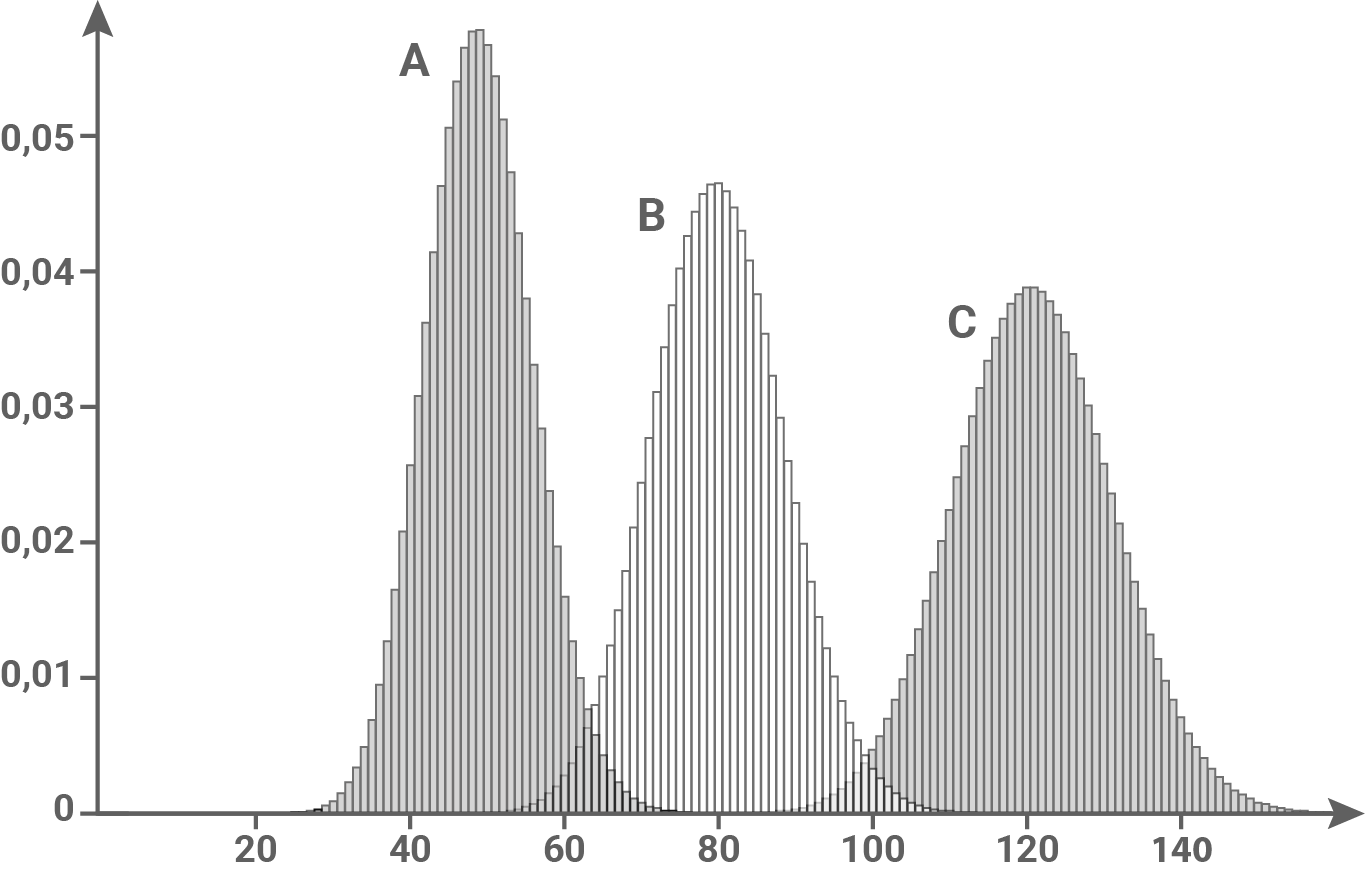
Die Wahrscheinlichkeit dafür, dass die Krankheit bei einem infizierten Menschen ausbricht, hängt von verschiedenen Faktoren (z. B. vom Immunsystem) ab. Die Abbildung zeigt für drei verschiedene Risikogruppen 
und 
für jeweils 
infizierte Menschen die Wahrscheinlichkeitsverteilung für die Anzahl der Menschen, bei denen die Krankheit ausbricht.
a)
Beurteile jede der beiden folgenden Aussagen:
I
Für die Risikogruppen 
und sind die Wahrscheinlichkeiten dafür, dass die Krankheit bei genau 
von infizierten Menschen ausbricht, etwa gleich groß.
II
Die Wahrscheinlichkeit dafür, dass die Krankheit ausbricht, ist für infizierte Menschen der Risikogruppe geringer als für infizierte Menschen der beiden anderen Risikogruppen.
(3 BE)
b)
Beurteile die folgende Behauptung:
Für binomialverteilte Zufallsgrößen mit den Parametern 
und 
mit 
nimmt die Varianz mit steigendem Wert von zu.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
a)
I+: Infektion
I-: keine Infektion
A+: Ausbruch der Krankheit
A-: kein Ausbruch der Krankheit
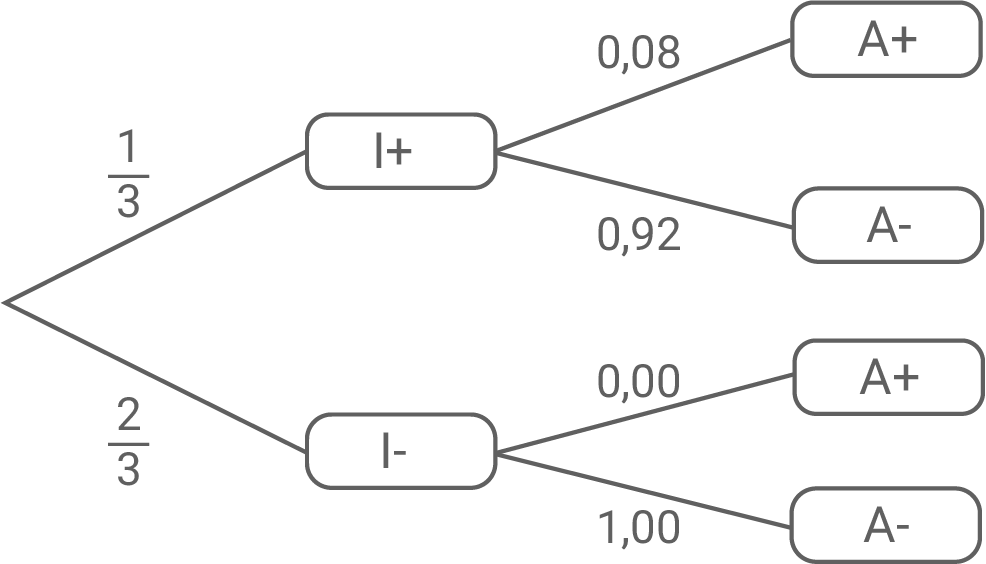
I-: keine Infektion
A+: Ausbruch der Krankheit
A-: kein Ausbruch der Krankheit
b)
Mit den Pfadregeln folgt:
Bei 
aller Menschen bricht die Krankheit im Laufe ihres Lebens nicht aus.
c)
Mit dem Satz von Bayes ergibt sich:
Somit beträgt die Wahrscheinlichkeit 
3.2
a)
Anzahl der Teilnehmenden
![\(\begin{array}[t]{rll}
E(X)&=& p\cdot n &\quad \scriptsize \mid\; :p \\[5pt]
\dfrac{E(X)}{p}&=& n \\[5pt]
600&=& n
\end{array}\)](https://mathjax.schullv.de/0522a101fad2739c918ae18ba4263845e61125259efa242db3a2e736ece4b675?color=5a5a5a)
Wahrscheinlichkeit
Es handelt sich um eine Binomialverteilung mit 
und 
Somit folgt:
Der Erwartungswert tritt mit einer Wahrscheinligkeit von 
ein.
b)
Es muss 
gelten. Durch systematisches Ausprobieren mit dem Taschenrechner folgt:
ist folglich eine mögliche Anzahl an Teilnehmenden.
3.3
a)
Es gilt: 
Aus der Abbildung lassen sich die Erwartungswerte ablesen. Die Wahrscheinlichkeiten folgen mit Hilfe der Formel.
![\(\begin{array}[t]{rll}
E(A)&=& 50 \\[5pt]
1000\cdot p_A &=& 50 &\quad \scriptsize \mid\;:1000 \\[5pt]
p_A&=& 0,05
\end{array}\)](https://mathjax.schullv.de/51be56ab306c9f2a1c5afbb4ddc1c1032d3335f4ee31a969d95d00a3818b9278?color=5a5a5a)
![\(\begin{array}[t]{rll}
E(B)&=& 80 \\[5pt]
1000\cdot p_B &=& 80 &\quad \scriptsize \mid\;:1000 \\[5pt]
p_B&=& 0,08
\end{array}\)](https://mathjax.schullv.de/b717bc580b0b73111a2a59fa33cb56f77c634e09960c9fbf1cb9ff2ee3c746a6?color=5a5a5a)
![\(\begin{array}[t]{rll}
E(C)&=& 121 \\[5pt]
1000\cdot p_B &=& 121 &\quad \scriptsize \mid\;:1000 \\[5pt]
p_C&=& 0,121
\end{array}\)](https://mathjax.schullv.de/63db2e2d9fcb49d01dd99adc0dd5ea2ec9116da9420d703f661e42c18c62a118?color=5a5a5a)
Aussage I ist wahr, da in der Abbildung zu erkennen ist, dass 
für die Risikogruppen und fast gleich ist.
Aussage II ist falsch, da 
ist.
b)
Für die Varianz gilt: 
Folglich ist die Behauptung richtig.