Aufgabe 1: Analysis
1.1
Die Abbildung 1 zeigt die Graphen der in  definierten Funktionen
definierten Funktionen  und
und  mit
mit  und
und  Die beiden Graphen haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der
Die beiden Graphen haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der  -Achse.
-Achse.
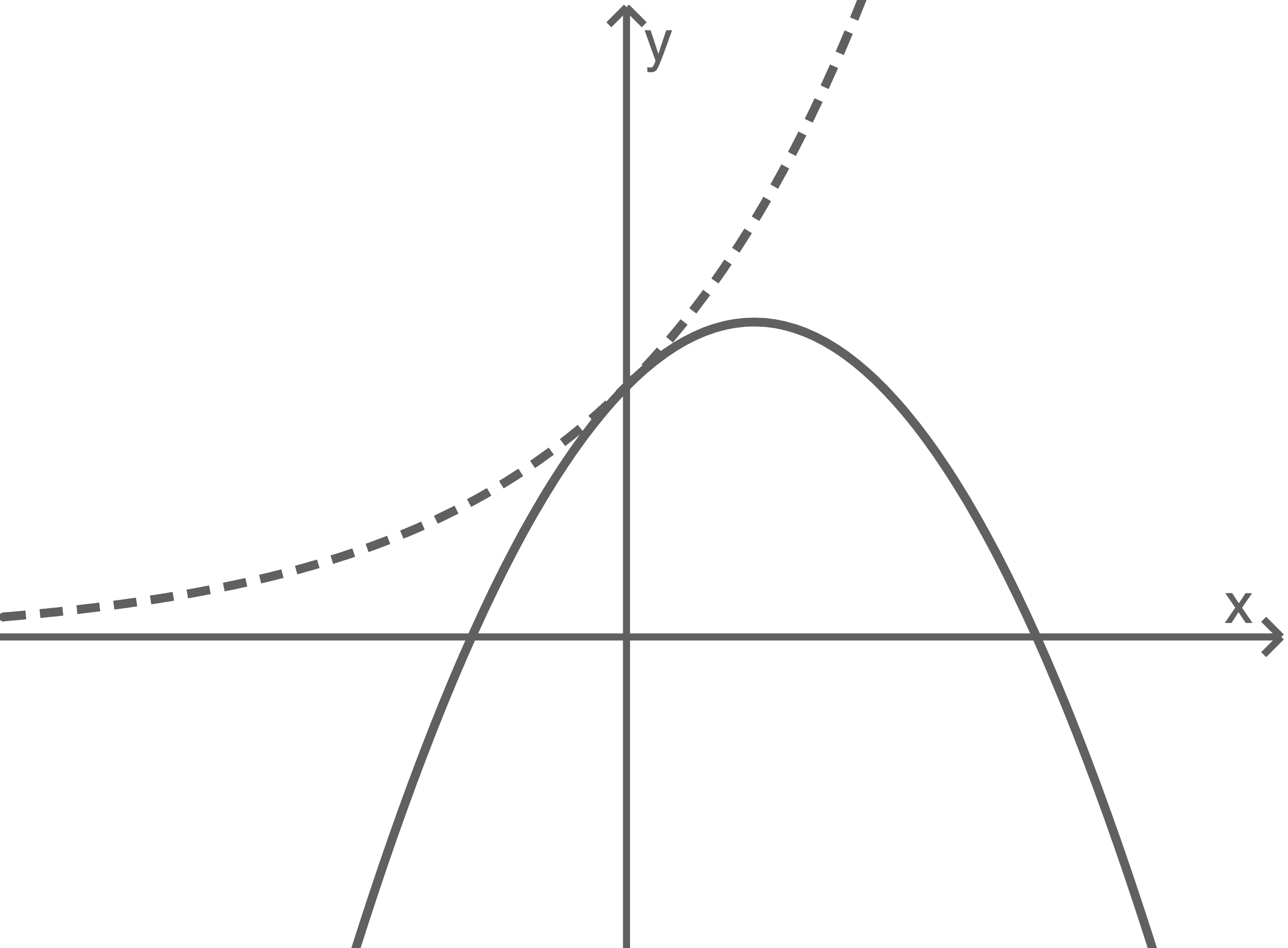
Abbildung 1
a)
Berechne die Nullstellen und die Extremstelle von 
(3 BE)
b)
Beschreibe, wie man den Abstand zwischen dem Graphen von  und der Gerade mit der Gleichung
und der Gerade mit der Gleichung  berechnen könnte.
berechnen könnte.
(2 BE)
c)
Berechne die Größe des Winkels, in dem der Graph von  die Gerade mit der Gleichung
die Gerade mit der Gleichung  schneidet.
schneidet.
(4 BE)
d)
Zeige, dass die Graphen von  und
und  in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
(4 BE)
e)
Berechne den Inhalt des Flächenstücks, das die Graphen von  und
und  und die Gerade mit der Gleichung
und die Gerade mit der Gleichung  begrenzen.
begrenzen.
(4 BE)
1.2
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen.
Die in  definierte Funktion
definierte Funktion  beschreibt für
beschreibt für  die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle.
Dabei ist
die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle.
Dabei ist  die seit Beobachtungsbeginn vergangene Zeit in Sekunden und
die seit Beobachtungsbeginn vergangene Zeit in Sekunden und  die momentane Durchflussrate in Kubikmetern pro Sekunde.
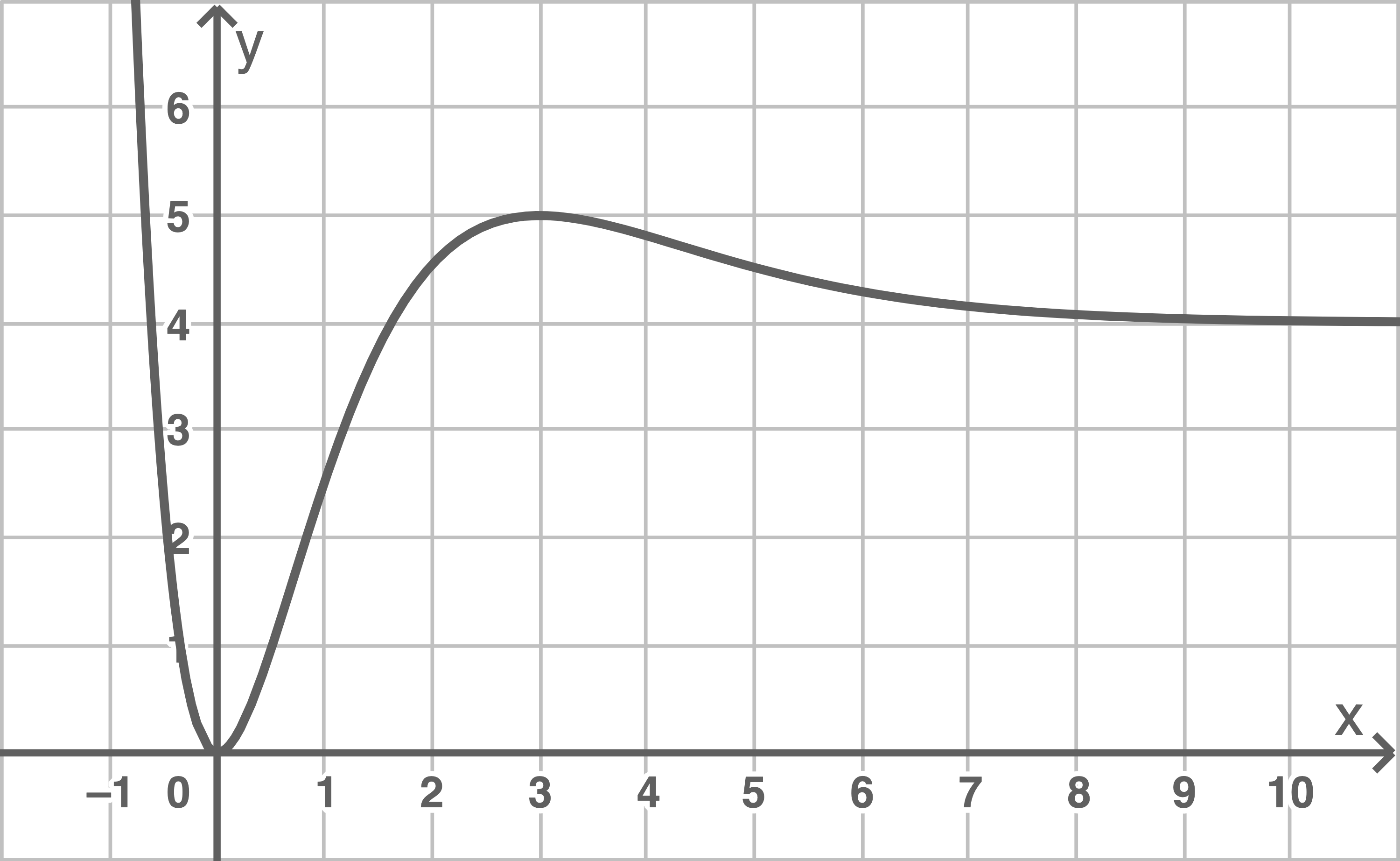
Die Abbildung 2 zeigt den Graphen von
die momentane Durchflussrate in Kubikmetern pro Sekunde.
Die Abbildung 2 zeigt den Graphen von 

Abbildung 2
a)
Ermittle mit Hilfe der Abbildung 2 das Volumen des Wassers, das vom Zeitpunkt vier Sekunden nach Beobachtungsbeginn bis zum Zeitpunkt sechs Sekunden nach Beobachtungsbeginn an der Messstelle vorbeifließt.
(3 BE)
b)
Bestimme für die ersten elf Sekunden nach Beobachtungsbeginn mit Hilfe der Abbildung 2 die momentane Durchflussrate für denjenigen Zeitpunkt, zu dem sie am stärksten abnimmt.
(3 BE)
c)
Die Tangente an den Graphen von  im Punkt
im Punkt  wird durch die Gleichung
wird durch die Gleichung  dargestellt.
Interpretiere die folgende Aussage im Sachzusammenhang:
Für alle Werte von
dargestellt.
Interpretiere die folgende Aussage im Sachzusammenhang:
Für alle Werte von  mit
mit  gilt
gilt 
1.3
Für jeden Wert von  ist eine in
ist eine in  definierte Funktion
definierte Funktion  mit
mit  gegeben.
Unabhängig von
gegeben.
Unabhängig von  sind 0 und 3 die einzigen Extremstellen von
sind 0 und 3 die einzigen Extremstellen von  Die Funktion
Die Funktion  ist die in der Aufgabe 1.2 betrachtete Funktion
ist die in der Aufgabe 1.2 betrachtete Funktion  die obige Abbildung zeigt also den Graphen von
die obige Abbildung zeigt also den Graphen von 
a)
Beschreibe den Einfluss des Parameters  auf den Graphen von
auf den Graphen von 
(1 BE)
b)
Bestimme denjenigen Wert von  für den der Mittelpunkt der Strecke zwischen den beiden Extrempunkten des Graphen von
für den der Mittelpunkt der Strecke zwischen den beiden Extrempunkten des Graphen von  auf der
auf der  -Achse liegt.
-Achse liegt.
(4 BE)
c)
Berechne den Wert des Terms  Gib alle Werte von
Gib alle Werte von  an, für die
an, für die  genau eine Nullstelle hat.
genau eine Nullstelle hat.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
a)
Nullstellen berechnen
![\(\begin{array}[t]{rll}
f(x)&=&0 \\[5pt]
-(x^2-x-1)&=&0 &\quad \scriptsize \mid\;\cdot(-1) \\[5pt]
x^2-x-1&=&0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/762b6155ff4b16ebe8e3061caa681f5ebb466c424524e0aa74b46a8f656f1652?color=5a5a5a) Mit der
Mit der  -Formel folgt:
-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1;2}&=&-\dfrac{(-1)}{2}\pm\sqrt{\left(\dfrac{-1}{2}\right)^2+1} \\[5pt]
x_{1;2}&=&\dfrac{1}{2}\pm\sqrt{\dfrac{5}{4}} \\[5pt]
x_1&\approx&1,62 \\[5pt]
x_2&\approx&-0,62
\end{array}\)](https://mathjax.schullv.de/1a3052645594e575c805d5166706692b98af5acf89bab6ec9c4ec8eab5e93fc1?color=5a5a5a) Extremstelle berechnen
Aus dem parabelförmigen Verlauf des Graphen von
Extremstelle berechnen
Aus dem parabelförmigen Verlauf des Graphen von  ergibt sich, dass die Extremstelle genau in der Mitte der beiden Nullstellen liegt. Es gilt also:
ergibt sich, dass die Extremstelle genau in der Mitte der beiden Nullstellen liegt. Es gilt also:
![\(\begin{array}[t]{rll}
x_E &=&\dfrac{1}{2}(x_1+x_2) & \\[5pt]
&=&\dfrac{1}{2}\left(\dfrac{1}{2}+\sqrt{\dfrac{5}{4}}+\dfrac{1}{2}-\sqrt{\dfrac{5}{4}}\right) & \\[5pt]
&=& \dfrac{1}{2}\left(\dfrac{1}{2}+\dfrac{1}{2}\right)& \\[5pt]
&=& \dfrac{1}{2}
\end{array}\)](https://mathjax.schullv.de/0e15e8535a4af11411caf17ee4bc034a41a6d1fdd25a9a1dc95558238e47c043?color=5a5a5a)
b)
Zunächst wird die  -Koordinate
-Koordinate  des Hochpunkts des Graphen von
des Hochpunkts des Graphen von  bestimmt.
Der Abstand folgt anschließend durch
bestimmt.
Der Abstand folgt anschließend durch 
c)
Es gilt:  Da der Schnittpunkt auf der Geraden
Da der Schnittpunkt auf der Geraden  liegen muss, gilt also
liegen muss, gilt also  und somit auch
und somit auch  Der Graph von
Der Graph von  schneidet die Gerade somit mit der Steigung 4.
Für den Schnittwinkel folgt also:
schneidet die Gerade somit mit der Steigung 4.
Für den Schnittwinkel folgt also:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& 4 \quad \scriptsize \mid \tan^{-1} \\[5pt]
\alpha&\approx& 76^\circ
\end{array}\)](https://mathjax.schullv.de/e2d687fa61d6588a48d7148fb4788f919e0bec510cc7742a42f56966523d05a3?color=5a5a5a)
d)
e)
2
a)
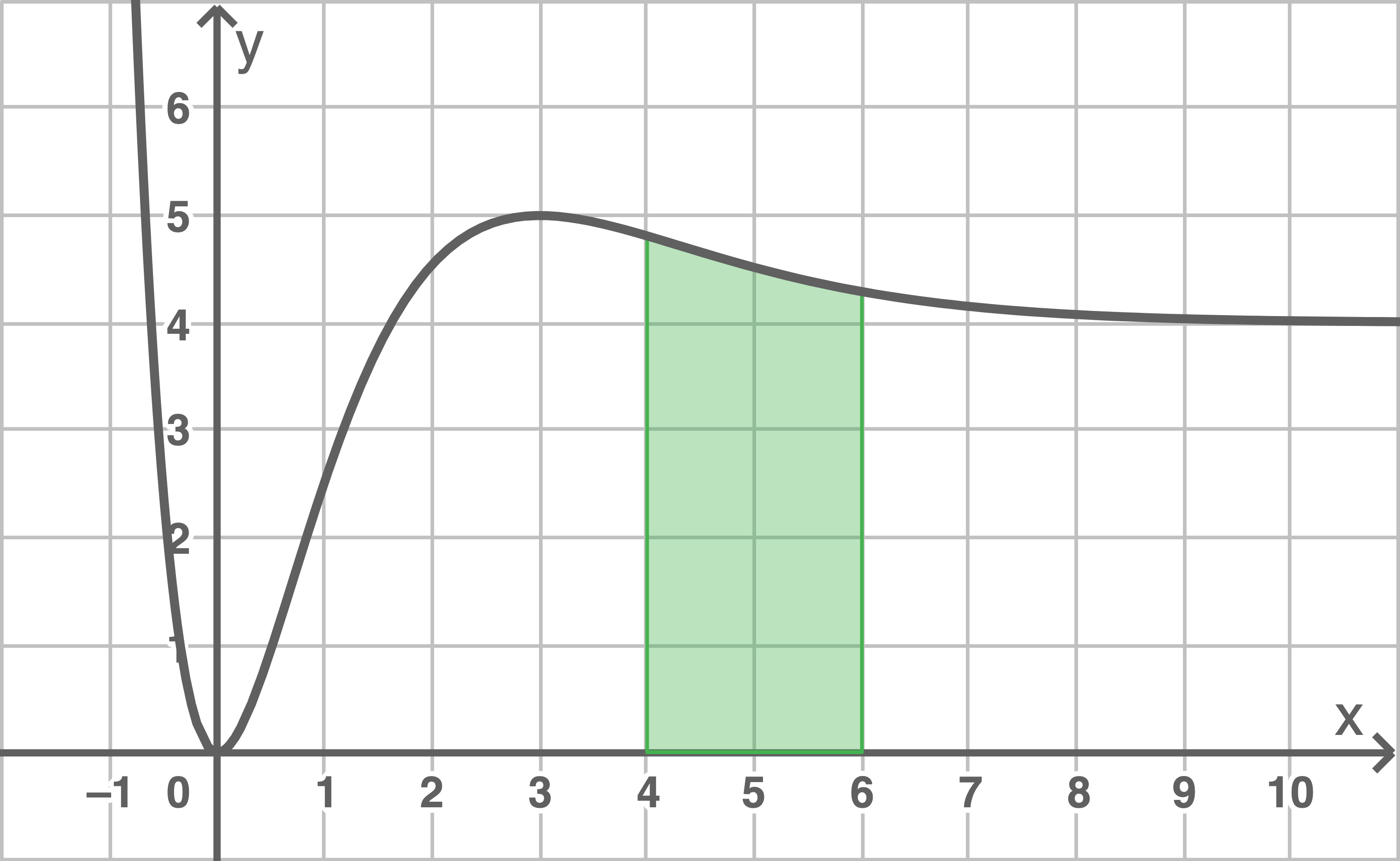
Im betrachteten Zeitraum fließen etwa  Wasser an der Messstelle vorbei.
Wasser an der Messstelle vorbei.
b)
Aus der Abbildung kann entnommen werden, dass der Graph für  an der Stelle
an der Stelle  am stärksten abnimmt.
Da
am stärksten abnimmt.
Da  die momentane Durchflussrate beschreibt, beträgt die momentane Durchflussrate zum betrachteten Zeitpunkt etwa
die momentane Durchflussrate beschreibt, beträgt die momentane Durchflussrate zum betrachteten Zeitpunkt etwa  .
.
c)
Für den angegebenen Zeitraum beschreibt die Tangente die zeitliche Entwicklung der momentanen Durchflussrate mit einer relativen Abweichung von weniger als 
1.3
a)
Der Parameter  verschiebt den Graphen von
verschiebt den Graphen von  entlang der
entlang der  -Achse.
-Achse.
b)
Die Extremstellen sind gegeben durch  und
und  Der Mittelpunkt
Der Mittelpunkt  der Strecke zwischen den beiden Extrempunkten besitzt somit die
der Strecke zwischen den beiden Extrempunkten besitzt somit die  -Koordinate
-Koordinate  Da
Da  auf der
auf der  -Achse liegen soll, gilt:
-Achse liegen soll, gilt:
c)
Wert berechnen
![\(\begin{array}[t]{rll}
w_4(3)&=& 4\cdot(3^2-3-1)\cdot \mathrm e^{-3}+4 & \\[5pt]
&\approx& 5 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ce212cc15177905dc2b969a6c7742da5fecc6135132df1036232df51a6d9d670?color=5a5a5a) Werte für
Werte für  angeben
Der Graph von
angeben
Der Graph von  hat genau eine Nullstelle, wenn der Tiefpunkt auf der
hat genau eine Nullstelle, wenn der Tiefpunkt auf der  -Achse liegt. Aus der Abbildung 2 geht hervor, dass dies für
-Achse liegt. Aus der Abbildung 2 geht hervor, dass dies für  der Fall ist.
Der Parameter
der Fall ist.
Der Parameter  verschiebt den Graphen von
verschiebt den Graphen von  entlang der
entlang der  -Achse. Für Werte von
-Achse. Für Werte von  kleiner als 4 besitzt der Graph somit mindestens 2 Nullstellen, für Werte größer als 4 besitzt der Graph keine Nullstelle.
kleiner als 4 besitzt der Graph somit mindestens 2 Nullstellen, für Werte größer als 4 besitzt der Graph keine Nullstelle.