Wahlpflichtaufgaben
5.1
Betrachtet wird die in 
definierte Funktion 
mit 
a)
Gib den Wertebereich von an.
(2 BE)
b)
Für die erste Ableitungsfunktion 
von gilt 
Die Graphen von und schneiden sich in einem Punkt.
Bestimme die Steigung des Graphen von in diesem Punkt.
(3 BE)
5.2
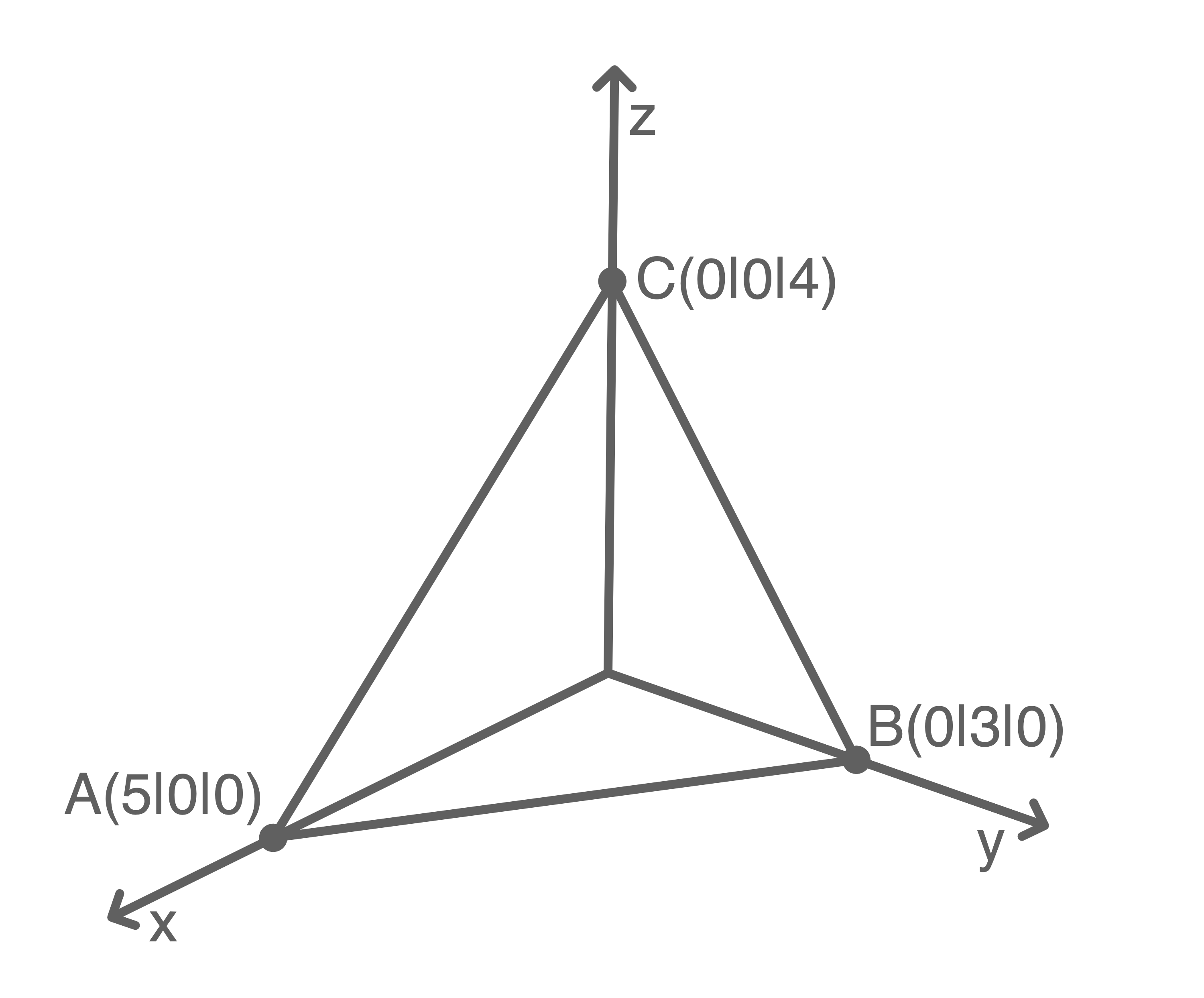
Die Abbildung zeigt das Dreieck 
Der Koordinatenursprung wird mit 
bezeichnet.
a)
Die Ebene, in der das Dreieck 
liegt, kann durch eine Gleichung der Form 
dargestellt werden.
Bestimme den Wert von 
(1 BE)
b)
Für jeden Wert von 
mit 
wird die Pyramide 
mit 
und 
betrachtet.
Bestimme denjenigen Wert von 
für den die Pyramide das größte Volumen hat.
(4 BE)
5.3
a)
Betrachtet werden die binomialverteilten Zufallsgrößen 
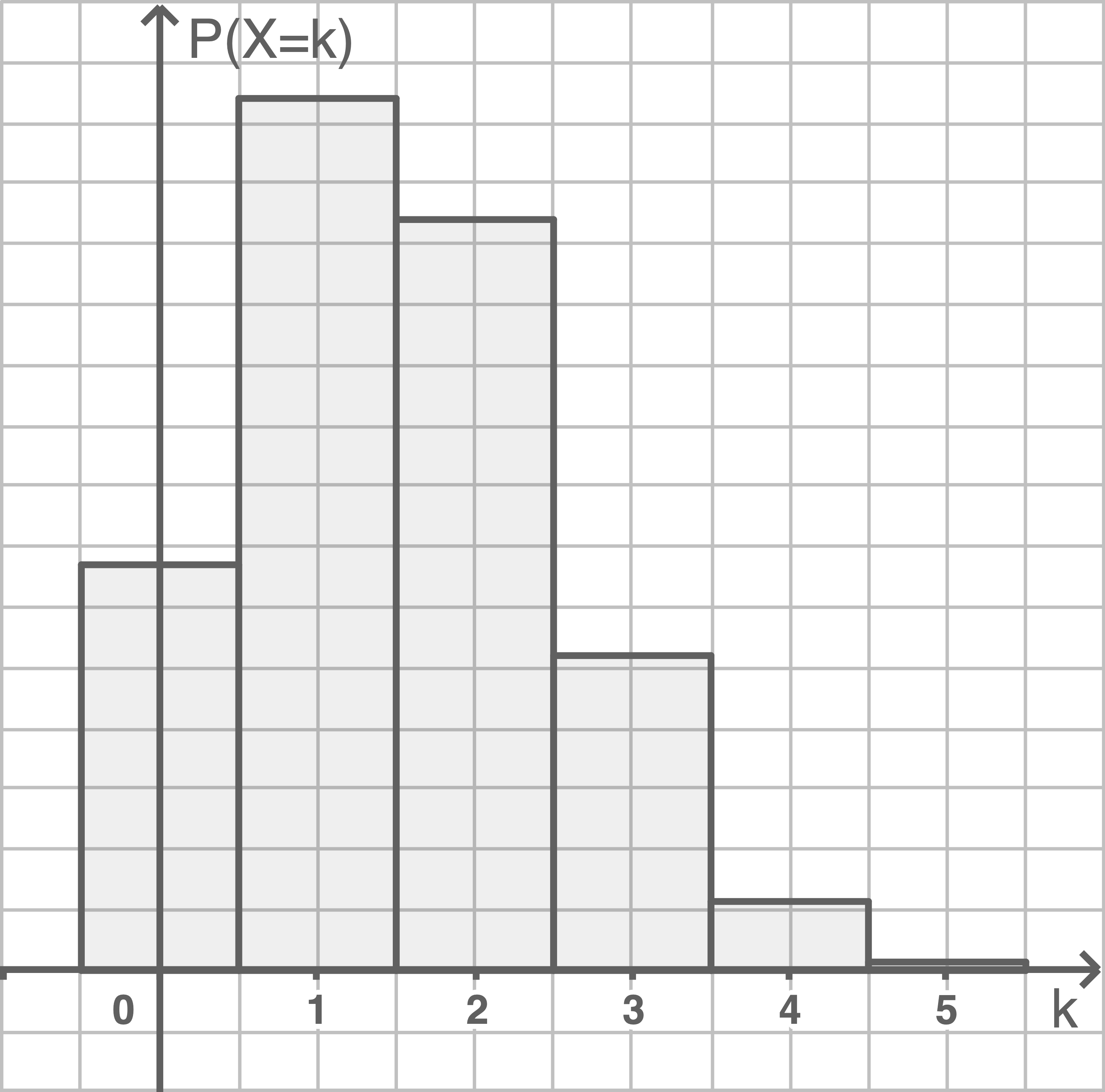
und 
In der Abbildung 1 ist die Wahrscheinlichkeitsverteilung von 
dargestellt.
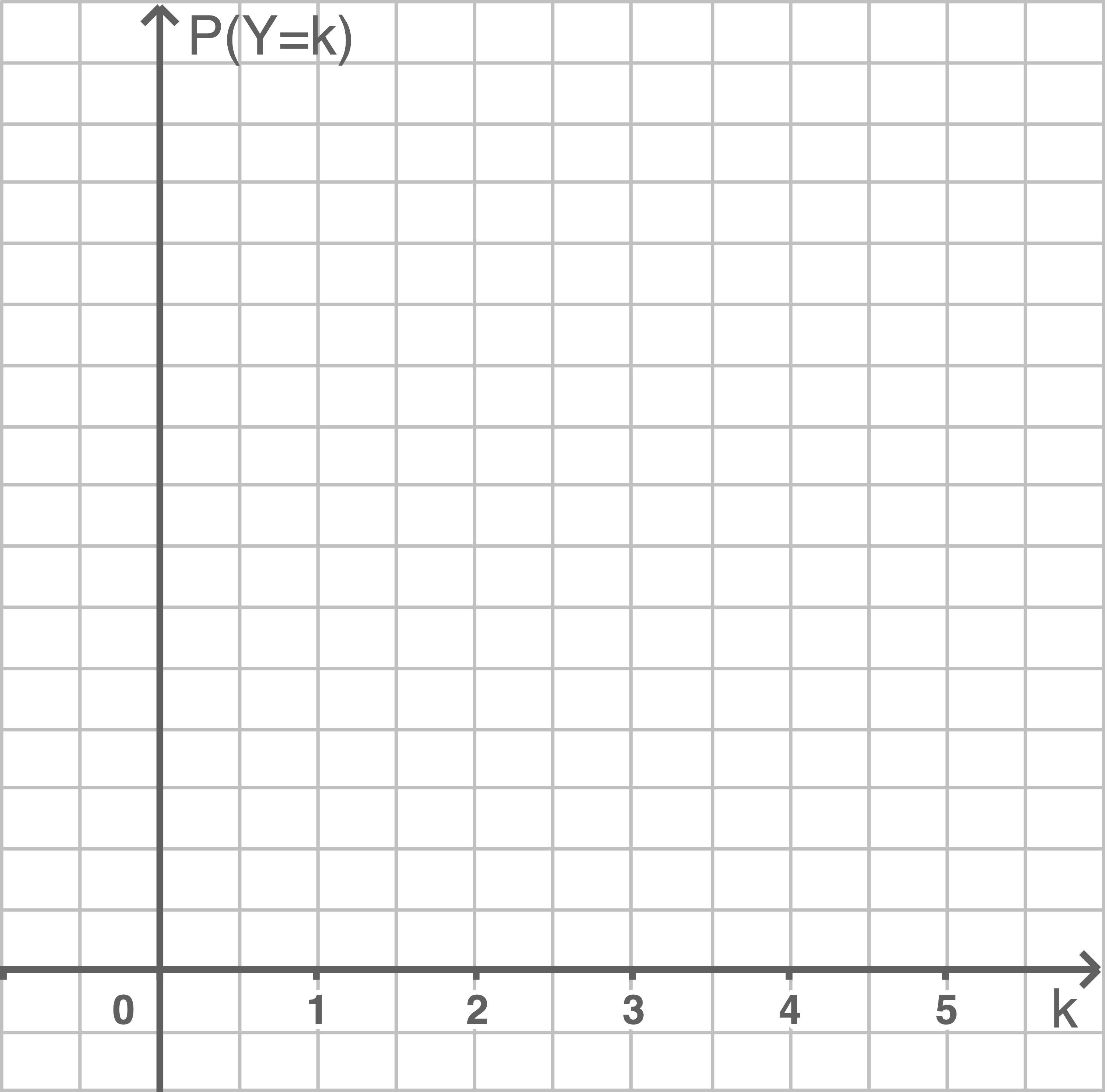Skizziere die Wahrscheinlichkeitsverteilung von 
in die Abbildung 2.
Abbildung 1
Abbildung 2
(2 BE)
b)
Beurteile folgende Aussage:
Für zwei Zufallsgrößen und mit 
und 
ist die Summe der zugehörigen Erwartungswerte gleich dem Stichprobenumfang.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
5.1
a)
Der Graph von ist durch den Exponenten 
achsensymmetrisch zur 
-Achse.
Da die Exponentialfunktion die -Achse bei 
schneidet und für positive Exponenten stets größer als 1 ist, ergibt sich der Wertebereich mit 
b)
1. Schritt: Schnittpunkt bestimmen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/99ce55a97b0d3c47f17e8066ad40f687676fd4561e7354f0e809c3bdf9af4bd2?color=5a5a5a)
2. Schritt: Steigung bestimmen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/cd246c8ca9ee397d8df1168827fbab3272113b71c75f40408f18a1fac2394dc6?color=5a5a5a)
5.2
a)
Einsetzen der Koordinaten von 
liefert:
![\(\begin{array}[t]{rll}
12\cdot 0+20\cdot 0+t\cdot 4&=& 60&\quad \scriptsize \mid\; :4 \\[5pt]
t&=& 15
\end{array}\)](https://mathjax.schullv.de/50ac2e442e1b5c666f3e32c417ba6505a9361d8b564bf295fc0fb47a1815e3b0?color=5a5a5a)
b)
Das Volumen der Pyramide ergibt sich durch 
Flächeninhalt 
der Grundfläche bestimmen:
![\(\begin{array}[t]{rll}
g&=&\dfrac{1}{2}\cdot x_A\cdot y_B & \\[5pt]
&=&\dfrac{1}{2}\cdot (5-k)\cdot (3+k)&\\[5pt]
&=& \dfrac{1}{2}\cdot (15+5k-3k-k^2)&\\[5pt]
&=& \dfrac{1}{2}\cdot (15+2k-k^2)
\end{array}\)](https://mathjax.schullv.de/991b9d6f44de7b3c7cc07aafff508423fd47914f49d8ed9d54b9559e868b18b5?color=5a5a5a)
Die Höhe 
des Dreiecks ist gegeben durch die 
-Koordinate von und beträgt somit unabhängig von 
stets 
Das größte Volumen der Pyramide entspricht dem Maximum von 
Es ergibt sich also:
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
0&=& \dfrac{4}{6}\cdot (2-2k)&\quad \scriptsize \mid\; : \dfrac{4}{6} \quad \scriptsize \mid\; +2k \\[5pt]
2k&=& 2 & \quad \scriptsize \mid\;:2 \\[5pt]
k&=& 1
\end{array}\)](https://mathjax.schullv.de/03a905d3d5d2101bcc107e76c8d86a5ead397fbdcbbcb9869e5c9b213583d0f8?color=5a5a5a)
Da aus der Aufgabenstellung hervorgeht, dass ein Wert für existiert, für den die Pyramide das größte Volumen hat, kann auf das Prüfen der hinreichenden Bedingung verzichtet werden.
5.3
a)
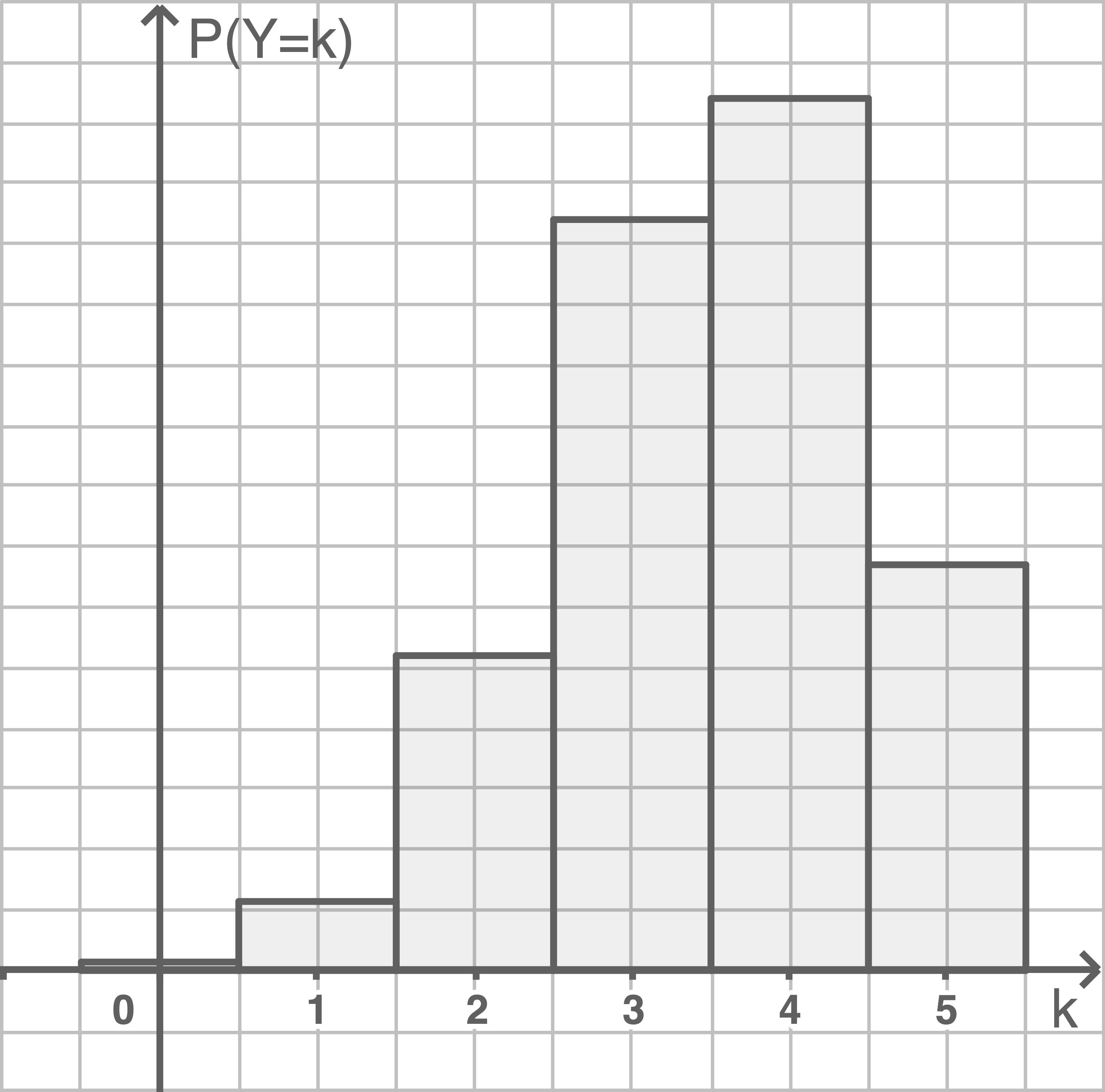
b)