Aufgabe 2 - Analytische Geometrie

2.1

In einem Koordinatensystem sind die Punkte $A(-1\mid 1\mid 2)$ , $B(-1\mid 5\mid 2)$ und $C(-4\mid 3\mid 3)$ gegeben. Das Dreieck $ABC$ stellt modellhaft ein Sonnensegel dar, das zwischen drei Masten gespannt ist. Der horizontale Untergrund wird durch die $xy$ -Ebene beschrieben. Eine Längeneinheit im Modell entspricht einem Meter in der Wirklichkeit.

Eine Gleichung der Ebene, die das Dreieck $ABC$ enthält, hat die Form $x+3z= j.$ Bestimme den Wert von $j$ .

1 BE

Damit Regenwasser gut abfließen kann, soll das Segel so gespannt sein, dass es eine Neigung von mindestens $30 \,\%$ aufweist.

Prüfe, ob diese Bedingung erfüllt ist.

4 BE

Die Seite des Segels, die parallel zum Untergrund verläuft, ist zum betrachteten Zeitpunkt $4 \,\%$ länger als vor dem ersten Aufspannen des Segels.

Berechne die Länge, die diese Seite vor dem ersten Aufspannen hatte.

3 BE

Auf das Segel trifft Sonnenlicht. Die zu den beiden unteren Eckpunkten des Segels gehörenden Eckpunkte seines Schattens auf dem Untergrund werden durch $\(A$ und $\(B$ dargestellt.

Ermittle im Modell die Koordinaten des Schattens des oberen Eckpunkts des Segels.

[Zur Kontrolle: $(-10\mid 6 \mid 0)$ ]

5 BE

Stelle den Schatten des Segels in der $xy$ -Ebene grafisch dar und bestimme seinen Flächeninhalt.

3 BE

2.2

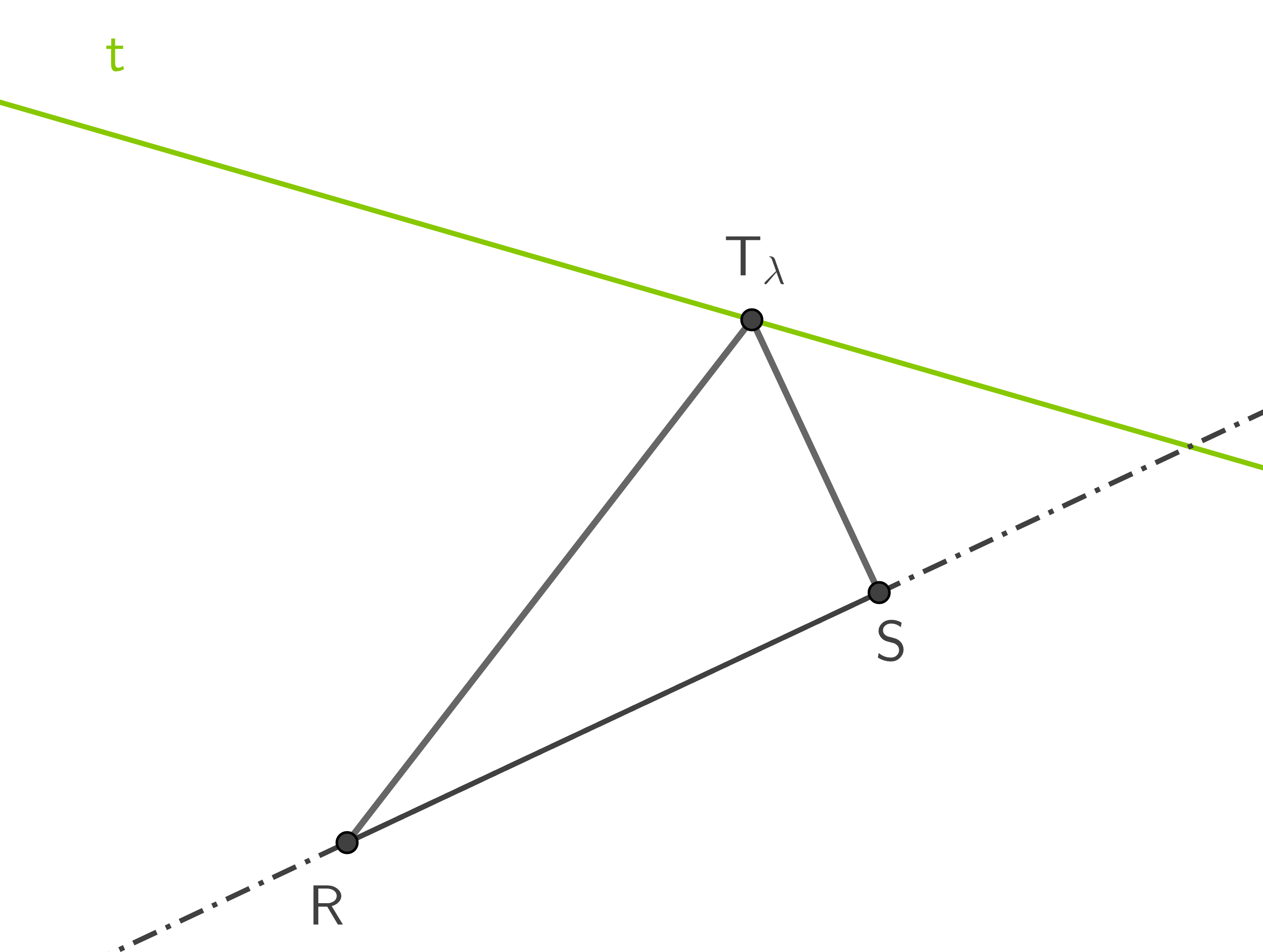
Die Abbildung zeigt die Gerade $t:\,\overrightarrow{x}=\pmatrix{-2\\3\\-1} + \lambda \cdot \pmatrix{-1\\0\\3}$ mit $\lambda \in \mathbb{R}$ , die die Gerade durch die Punkte $R(-1\mid 2\mid 3)$ und $S(-1\mid 4\mid 3)$ nicht schneidet. Zu jedem Wert von $\lambda$ gehört ein Punkt $T_\lambda$ von $t$ . Jeder Punkt $T_\lambda$ hat von $R$ und $S$ den gleichen Abstand.
Unter den Dreiecken $RST_\lambda$ hat eines den kleinsten Flächeninhalt.

Begründe, dass der zugehörige Wert von $\lambda$ die Lösung der folgenden Gleichung ist.

$\pmatrix{-1-\lambda\\ 0\\-4+3\lambda} \circ \pmatrix{-1\\0\\3}= 0$

Geometrische Darstellung mit Punkten R, S und T auf Linien t und Tλ.

4 BE

2.1

Setze die Koordinaten eines der drei Punkte in die Koordinatengleichung ein.

Punkt A:

$\begin{array}[t]{rll} (-1)+3\cdot 2&=& j\\[5pt] 5&=&j \end{array}$

Ein Normalenvektor der xy-Ebene ist $\overrightarrow{n}=\pmatrix{0\\0\\1}$ , ein Normalenvektor der Dreiecksebene lässt sich aus der Ebenengleichung ablesen und ist demnach $\overrightarrow{n_E}=\pmatrix{1\\0\\3}$ .

Die Größe des Winkels zwischen zwei Ebenen lässt sich wie folgt berechnen:

$\begin{array}[t]{rll} \cos(\alpha) &=& \dfrac{\pmatrix{1\\0\\3} \circ \pmatrix{0\\0\\1}}{\left|\pmatrix{1\\0\\3}\right| \cdot \left|\pmatrix{0\\0\\1}\right|} \\[5pt] &=&\dfrac{3}{\sqrt{1^2+3^2} \cdot\sqrt{1^2}}&\quad \scriptsize \mid\; \cos^{-1} \\[5pt] \alpha &\approx& 18,43^{\circ} \\[5pt] \end{array}$

Für die Steigung gilt $m= \tan(\alpha)$ $= \tan(18,43^{\circ} )$ $\approx 0,33 = 33\%$

Somit ist die Neigung größer als 30 % und die Bedingung erfüllt.

Die Seite, die parallel zum Untergrund liegt, wird durch $\overrightarrow{AB}$ beschrieben.

$\begin{array}[t]{rll} \left|\overrightarrow{AB}\right|&=& \left|\pmatrix{0\\4\\0} \right| \\[5pt] &=& 4 \end{array}$

Das Segel ist zum betrachteten Zeitpunkt also 4 m lang. Dies entspricht 104 % der ursprünglichen Länge:

$4\, \text{m} :1,04 \approx 3,85\, \text{m}$

Die Seite des Segels war ursprünglich 3,85 m lang.

Die Sonnenstrahlen verlaufen in Richtung des Vektors $\(\overrightarrow{AA$ Der Schattenpunkt $\(C$ liegt daher auf der Geraden mit der Gleichung:

$\(\begin{array}[t]{rll} h: \, \overrightarrow{x} &=& \overrightarrow{OC} + s\cdot \overrightarrow{AA$

$\(C$ liegt außerdem in der xy-Ebene. Für die z-Koordinate folgt also:

$\begin{array}[t]{rll} 3-2s&=&0 &\quad \scriptsize \mid -3 \; \\[5pt] -2s&=&-3 &\quad \scriptsize \mid :(-2) \; \\[5pt] s&=& \dfrac{3}{2} \\[5pt] \end{array}$

Einsetzen in die Geradengleichung:

$\(\overrightarrow{OC$

$\(C$ hat damit die Koordinaten $(-10\mid 6\mid 0).$

Dreieck im Koordinatensystem mit Punkten A', B' und C' sowie einer schattierten Fläche.

$\(\begin{array}[t]{rll} A &=& \frac{1}{2}\cdot \left|\overrightarrow{A$

Der Schatten des Segels besitzt einen Flächeninhalt von $10\,\text{m}^2.$

2.2

Der Flächeninhalt des Dreiecks hängt von der Länge der Grundseite und der Länge der zugehörigen Höhe ab.
Da jeder Punkt $T_{\lambda}$ von $R$ und $S$ den gleichen Abstand besitzt, ist das Dreieck $RST_{\lambda}$ gleichschenklig.
Betrachte $\overline{RS}$ als Grundseite des Dreiecks. Die zugehörige Höhe verläuft dann vom Mittelpunkt $M$ der Seite $\overline{RS}$ zum Punkt $T_{\lambda}.$
Die Länge der Grundseite bleibt immer gleich. Abhängig vom Wert $\lambda$ verändert sich aber die Höhe.
Das Dreieck mit dem kleinsten Flächeninhalt ist also das Dreieck, für das die Höhe des Dreiecks am kleinsten ist. Gesucht ist also der Punkt $T_{\lambda}$ auf der Geraden $t,$ der von $M$ den kleinsten Abstand hat.
Dies ist der Punkt, für den die Strecke $\overline{MT_{\lambda}}$ senkrecht zur Geraden $t$ verläuft.

Die Koordinaten von $M$ ergeben sich zu:

$\overrightarrow{OM} = \frac{1}{2} \cdot \left( \overrightarrow{OR}+ \overrightarrow{OS} \right) = \pmatrix {-1\\3\\3}$

Daraus folgt:

$\overrightarrow{MT_{\lambda}} = \pmatrix{-1-\lambda\\0\\-4+3\lambda}$

Der Richtungsvektor von $t$ ist $\pmatrix{-1\\0\\3}.$

Der Richtungsvektor von $t$ und $\overrightarrow{MT_{\lambda}}$ müssen senkrecht zueinander stehen, das ist der Fall, wenn ihr Skalarprodukt Null ergibt:

Mit der Gleichung $\pmatrix{-1-\lambda\\0\\-4+3\lambda} \circ \pmatrix{-1\\0\\3} = 0$ lässt sich also der zugehörige Wert von $\lambda$ bestimmen.