Pflichtaufgaben

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ durch $f(x)=\dfrac{1}{2}x^2+1$ .
In der Abbildung sind der Graph der Funktion $f$ sowie der Graph einer linearen Funktion $g$ dargestellt.

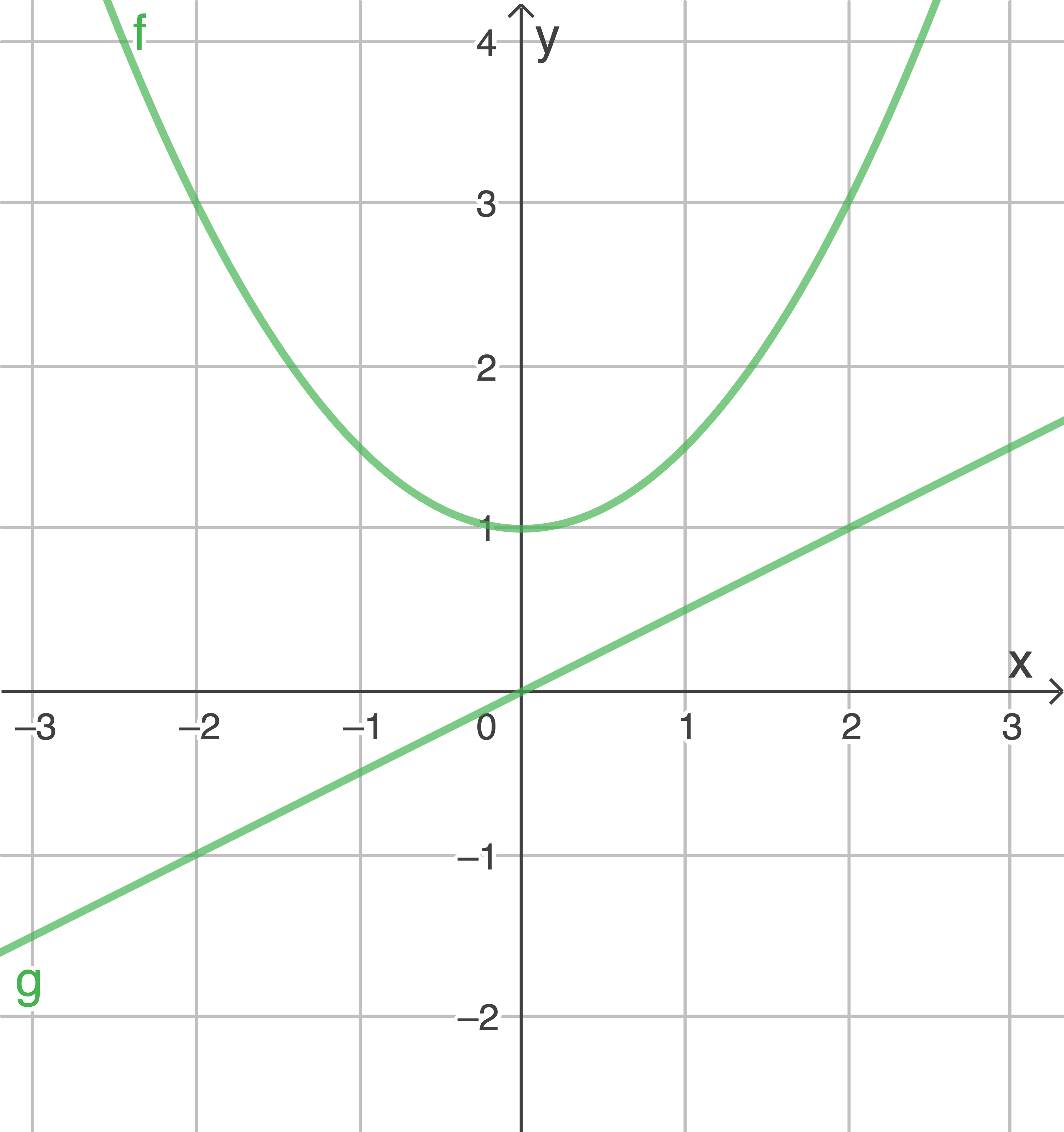
Graph einer Parabel und einer Geraden im Koordinatensystem.

Gib eine Gleichung der Funktion $g$ an.

(1 BE)

Bestimme die Nullstelle der Funktion $p$ mit $p(x)=f(x)\cdot g(x)$ .

(2 BE)

Skizziere den Graphen der Funktion $p$ im Intervall $-2 \leq x \leq 2$ in der Abbildung.

(2 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^3-x$ .

Einer der folgenden Graphen I, II und III stellt $f$ dar. Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.

Graph einer mathematischen Funktion mit den Achsen x und y.

Graf einer mathematischen Funktion mit x- und y-Achse, zeigt eine grüne Kurve.

Graph einer Funktion mit x- und y-Achse, zeigt eine steigende Kurve.

(2 BE)

Berechne den Inhalt der Fläche, die der Graph von $f$ und die $x$ -Achse einschließen.

(3 BE)

Gegeben sind der Punkt $P(-3\mid 16\mid -10)$ , die Gerade $g:\overrightarrow{x}=\pmatrix{1\\0\\2}+r\cdot \pmatrix{-1\\4\\-3}$ mit $r\in\mathbb{R}$ und die Ebene $E:x-4y+3z=20$ .

Weise nach, dass $P$ auf $g$ liegt.

(1 BE)

Zeige, dass $g$ senkrecht zur Ebene $E$ verläuft.

(1 BE)

Unter allen Punkten der Ebene $E$ hat der Punkt $Q$ den kleinsten Abstand von $P$ .
Ermittle die Koordinaten von $Q$ .

(3 BE)

Ein Autohändler besitzt vier Mal so viele Gebrauchtwagen wie Neuwagen. Erfahrungsgemäß verkauft er an Aktionstagen $10\,\%$ der Neuwagen. Von allen Wagen werden etwa $60\,\%$ an diesen Aktionstagen verkauft.

Stelle den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.

(3 BE)

Beurteile die folgende Aussage:
„Mehr als die Hälfte der Gebrauchtwagen werden an diesen Aktionstagen verkauft.“

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Gerade $g$ besitzt die Steigung $m=\dfrac{1}{2}$ und verläuft durch den Koordinatenursprung.

$g(x)=\dfrac{1}{2}x$

$\begin{array}[t]{rll} p(x)&=&f(x)\cdot g(x) \\[5pt] &=&\left(\frac{1}{2}x^2+1\right)\cdot \dfrac{1}{2}x\\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgt, dass $p(x)=0$ für $x =0$ oder $\frac{1}{2}x^2+1 =0$ erfüllt ist.

$\begin{array}[t]{rll} \frac{1}{2}x^2+1&=&0 &\quad \mid \; -1\\[5pt] \frac{1}{2}x^2 &=& -1 &\quad \scriptsize \mid\; \cdot 2\\[5pt] x^2 &=& -2 \end{array}$

Da $x^2$ nicht negativ sein kann, ist $x=0$ die einzige Nullstelle der Funktion $p.$

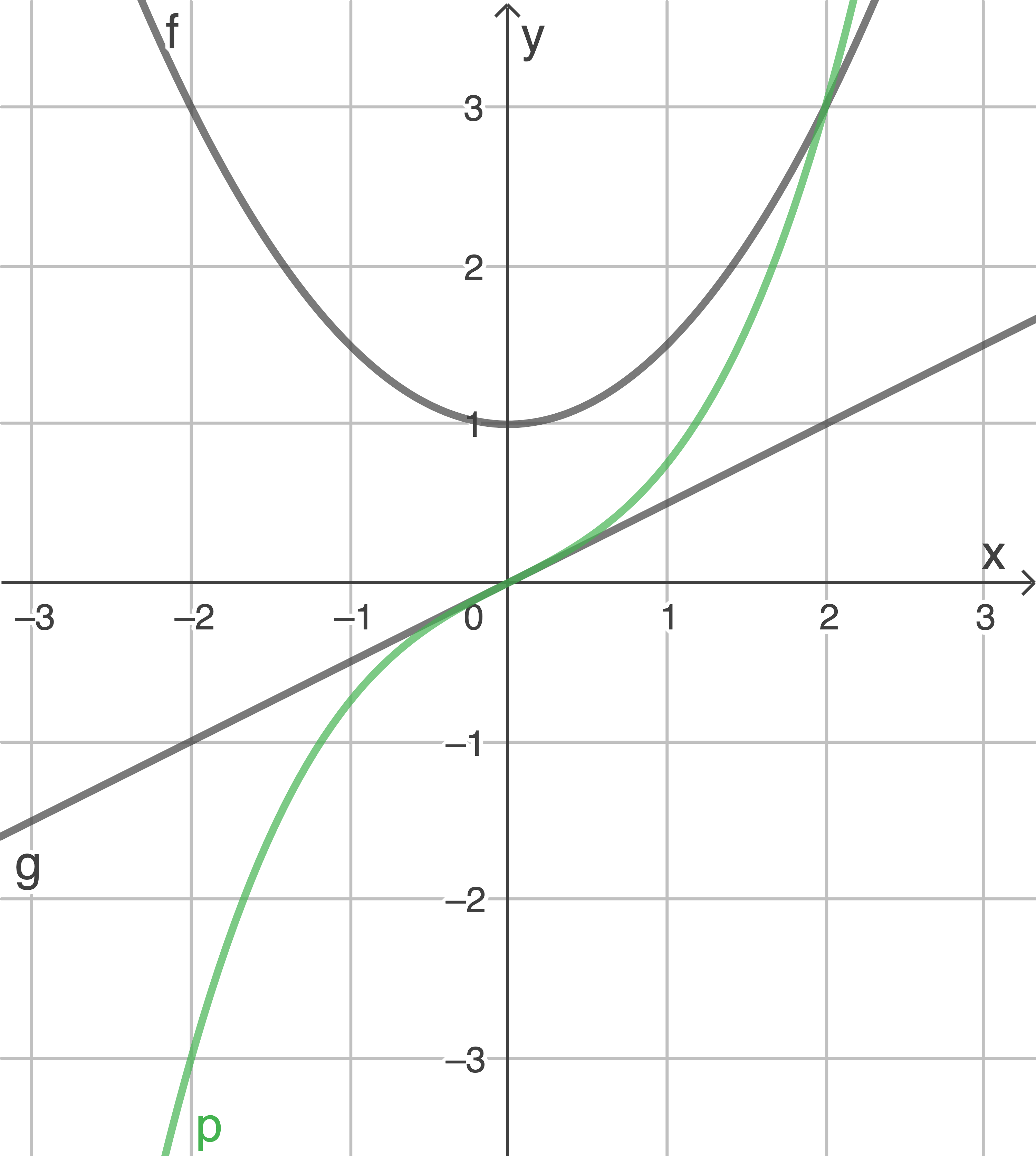
Grafik mit zwei Funktionen: eine graue Parabel und eine grüne Linie, dargestellt im Koordinatensystem.

Graph II:

$f(0,5)=0,5^3-0,5\lt0$

Da $f(0,5)\lt0$ gilt, kommt der Graph II nicht infrage.

Graph III:

Der Graph III kommt nicht infrage, da die Steigung des Graphen von $f$ für $-0,5\leq x\leq0,5$ nicht konstant ist.

Vollständigen Rechenweg anzeigen

Der gesuchte Flächeninhalt beträgt $\dfrac{1}{2}$

$\begin{array}[t]{rll} \pmatrix{-3\\16\\-10}&=&\pmatrix{1\\0\\2}+4\cdot \pmatrix{-1\\4\\-3} \\[5pt] \end{array}$

Die Koordinaten von $P$ erfüllen also für $r=4$ die Geradengleichung von $g.$ $P$ liegt somit auf $g.$

Ein Normalenvektor von $E$ ist $\overrightarrow{n_E}=\pmatrix{1\\-4\\3},$ ein Richtungsvektor von $g$ ist $\overrightarrow{r_g} = \pmatrix{-1\\4 \\ -3}.$

$\pmatrix{1\\-4\\3}=(-1)\cdot \pmatrix{-1\\4\\-3}$

Der Normalenvektor der Ebene $E$ und der Richtungsvektor der Geraden $g$ sind Vielfache voneinander und somit linear abhängig bzw. parallel. Daher verläuft die Gerade $g$ senkrecht zu $E.$

Da $P$ auf der Geraden $g$ liegt, die senkrecht zur Ebene $E$ verläuft, muss $Q$ der Schnittpunkt von $g$ und $E$ sein. $Q$ liegt also auch auf $g$ und hat demnach die Koordinaten: