Pflichtaufgabe 1 - Analysis
Gegeben ist die Funktion  mit
mit  ,
,  . Ihr Graph sei
. Ihr Graph sei  .
.
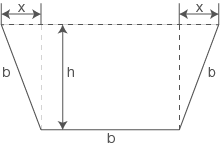 Abb. 1Abbildung (nicht maßstäblich)
Zeige, dass
Abb. 1Abbildung (nicht maßstäblich)
Zeige, dass  Gleichung einer Zielfunktion
Gleichung einer Zielfunktion  dieser Extremwertproblematik ist und gib einen zugehörigen Definitionsbereich für diese Funktion an.
dieser Extremwertproblematik ist und gib einen zugehörigen Definitionsbereich für diese Funktion an.
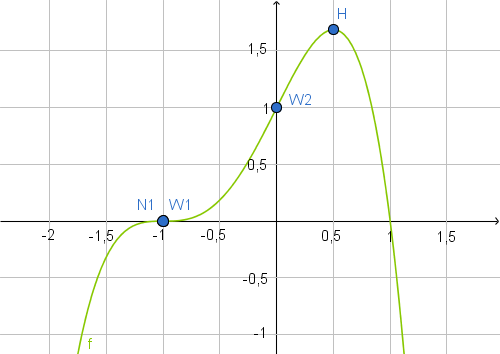
Die Funktion besitzt genau eine lokale Extremstelle und zwar die Maximumstelle
besitzt genau eine lokale Extremstelle und zwar die Maximumstelle  .
.
Ermittle die Höhe der Rinne mit maximaler Querschnittsfläche.
der Rinne mit maximaler Querschnittsfläche.
a)
Ermittle die Nullstellen der Funktion  und untersuche das Verhalten der Funktion
und untersuche das Verhalten der Funktion  für
für  .
.
Der Graph besitzt genau einen lokalen Extrempunkt und genau zwei Wendepunkte. Weise nach, dass der Punkt
besitzt genau einen lokalen Extrempunkt und genau zwei Wendepunkte. Weise nach, dass der Punkt  dieser lokale Extrempunkt ist und bestimme die Art des Extremums.
dieser lokale Extrempunkt ist und bestimme die Art des Extremums.
Berechne die Koordinaten der Wendepunkte des Graphen .
.
Zeichne den Graphen im Intervall
im Intervall  .
.
Der Graph schließt mit der
schließt mit der  -Achse eine Fläche vollständig ein.
-Achse eine Fläche vollständig ein.
Ermittle mithilfe des Hauptsatzes der Differential- und Integralrechnung die Maßzahl des Inhalts dieser Fläche.
Der Graph
[zur Kontrolle:  ]
]
Berechne die Koordinaten der Wendepunkte des Graphen
Zeichne den Graphen
Der Graph
Ermittle mithilfe des Hauptsatzes der Differential- und Integralrechnung die Maßzahl des Inhalts dieser Fläche.
b)
Die Abbildung zeigt den Querschnitt einer Rinne, die aus drei Brettern der gleichen Breite  gebildet werden soll.
gebildet werden soll.
Die Querschnittsfläche dieser Rinne hat die Form eines Trapezes und soll maximal werden.
Die Querschnittsfläche dieser Rinne hat die Form eines Trapezes und soll maximal werden.
 Abb. 1Abbildung (nicht maßstäblich)
Abb. 1Abbildung (nicht maßstäblich)
Die Funktion
Ermittle die Höhe
c)
Für alle Funktionen  mit
mit ![\(z(x)=[g(x)]^2\)](https://mathjax.schullv.de/52d54c528ee11fc26bb91fd3801e4258d1de51579aace242d07fb92cc5912da7?color=5a5a5a) , wobei
, wobei  eine differenzierbare Funktion ist, gilt nach der Kettenregel
eine differenzierbare Funktion ist, gilt nach der Kettenregel  .
.
Begründe, dass folgende Aussage falsch ist:
Jede lokale Extremstelle von ist auch lokale Extremstelle von
ist auch lokale Extremstelle von  .
.
Bildnachweise [nach oben]
Begründe, dass folgende Aussage falsch ist:
Jede lokale Extremstelle von
© 2016 - SchulLV.
a)
Ein Produkt ist genau dann Null, wenn einer der Faktoren Null ist.
Löse also die beiden Gleichungen - Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Ist
, handelt es sich um eine Minimalstelle.
- Ist
, handelt es sich um eine Maximalstelle.
- Ist
- Bestimme die ersten beiden Ableitungsfunktionen
und
.
- Wende das notwendige Kriterium an, indem du
setzt und nach
löst.
- Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in
einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
- Berechne die Funktionswerte von
an den Extremstellen.
b)
c)
© 2016 - SchulLV.