Pflichtaufgaben
1
Gegeben ist die in 
definierte Funktion 
mit 
a)
Begründe, dass der Graph von symmetrisch bezüglich des Koordinatenursprungs ist.
(1 BE)
b)
Der Graph von und die 
-Achse schließen eine Fläche ein, die aus zwei Flächenstücken besteht.
Berechne den Inhalt dieser Fläche.
(4 BE)
2
Gegeben sind die Gerade 
durch die Punkte 
und 
sowie die in der Abbildung dargestellte Gerade 
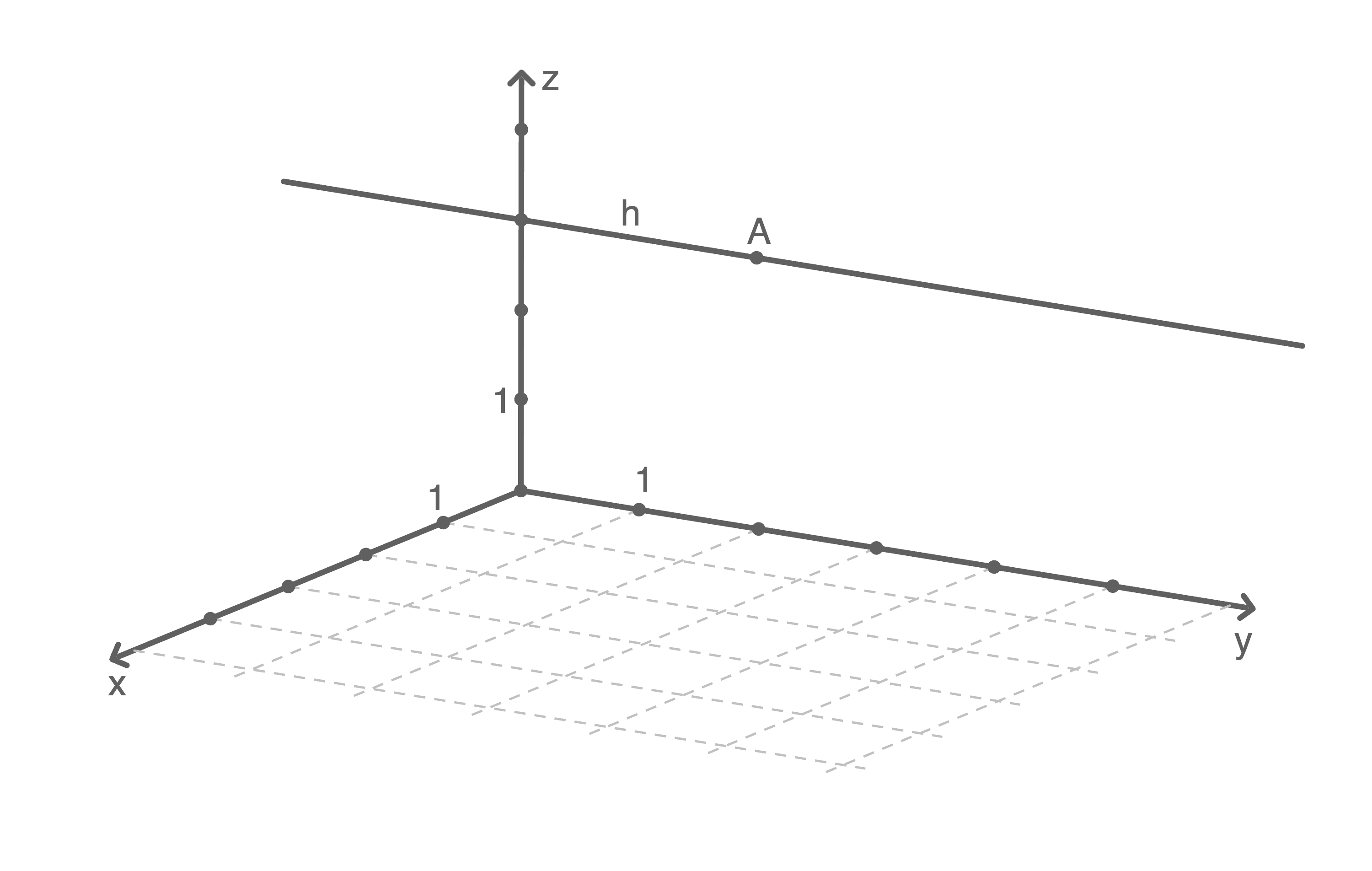
a)
Zeichne die Gerade in das abgebildete Koordinatensystem ein.
(1 BE)
b)
Begründe , dass und 
sich nicht in 
schneiden.
(2 BE)
c)
Für 
beschreibt 
eine Strecke.
Bestimme die Koordinaten des Mittelpunkts dieser Strecke.
(2 BE)
3
In einem Spielwarengeschäft erhält jedes Kind im Rahmen einer Werbeaktion einen kleinen, blickdicht verpackten Ball. Die Wahrscheinlichkeit dafür, dass dieser Ball eine Glitzerfärbung hat, beträgt 
a)
Zeige, dass die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen Ball mit Glitzerfärbung erhält, kleiner als 
ist.
(2 BE)
b)
Beschreibe im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term 
berechnet werden kann.
Gib dieses Ereignis an.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Die gegebene Funktion ist symmetrisch bezüglich des Koordinatenursprungs, da sie ausschließlich ungerade Exponenten besitzt.
b)
Nullstellen berechnen:
![\(\begin{array}[t]{rll}
f(x) &=& 0& \\[5pt]
x^3 - 4x &=& 0& \\[5pt]
x\cdot (x^2-4) &=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/daccbd3fff4c407935a8a7e57f107fa259c4bc5632b58ae52118f9148ea2e884?color=5a5a5a)
Mit dem Satz vom Nullprodukt folgt direkt 
Die weiteren Nullstellen ergeben sich zu:
![\(\begin{array}[t]{rll}
x^2-4&=& 0&\quad \scriptsize \mid\; +4\\[5pt]
x^2&=& 4&\quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
x_{2;3 }&=& \pm 2
\end{array}\)](https://mathjax.schullv.de/c69beaa53cdda62fa6fc0cc3fd3d5f0ea4912666d01d0f5c23986be773fafdc2?color=5a5a5a)
Da der Graph von symmetrisch zum Ursprung ist, folgt:
Der Inhalt der eingeschlossenen Fläche entspricht somit 8 Flächeneinheiten.
2
a)
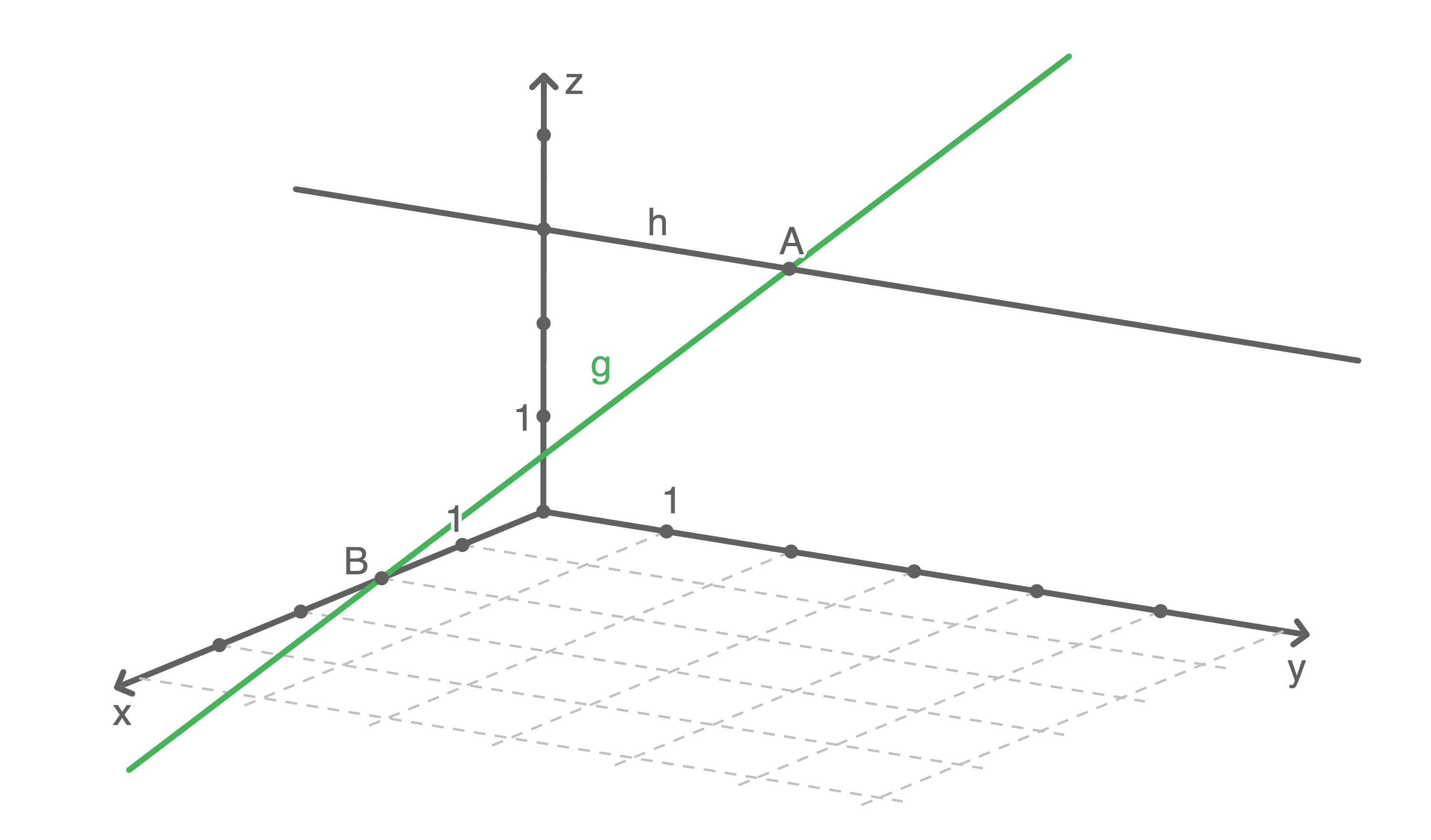
b)
Der Punkt liegt laut Aufgabenstellung auf der Geraden 
Punktprobe mit und der Geradengleichung von liefert:
![\(\begin{array}[t]{rll}
\pmatrix{0\\2\\3}&=& \pmatrix{-2\\0\\2}+t\cdot \pmatrix{0\\1\\0} & \\[5pt]
\pmatrix{0\\2\\3}&=& \pmatrix{-2\\t\\2}
\end{array}\)](https://mathjax.schullv.de/f329b8efdf873f0205d3abfb2b39eebb4f043d2faaa8333975f4bab7bcddfc54?color=5a5a5a)
Die erste und dritte Zeile führt direkt zu einem Widerspruch.
Somit liegt der Punkt nicht auf der Geraden und die beiden Geraden schneiden sich folglich nicht in 
c)
Die Punkte, die auf der Strecke liegen, haben die Koordinaten 
mit 
Die 
-Koordinate des Mittelpunkts ergibt sich zu 
Der Mittelpunkt besitzt somit die Koordinaten 
3
a)
b)
Zufallsexperiment beschreiben
Vier Kinder erhalten im Spielwarengeschäft jeweils einen kleinen, blickdicht verpackten Ball, wobei dieser mit einer Wahrscheinlichkeit von 
eine Glitzerfärbung hat. Die Wahrscheinlichkeit, einen Ball mit Glitzerfärbung zu erhalten, bleibt stets gleich groß.
Ereignis beschreiben
Der Term 
beschreibt das Ereignis, dass unter den vier erhaltenen Bällen kein Glitzerball ist.
Der Term 
beschreibt das Ereignis, dass unter den vier gezogenen Bällen genau ein Glitzerball ist.
Insgesamt beschreibt der Term also das Ereignis, dass höchstens einer der vier erhaltenen Bälle eine Glitzerfärbung hat.