Lerninhalte in Mathe

Abi-Aufgaben gA

Digitales Schulbuch

Inhaltsverzeichnis

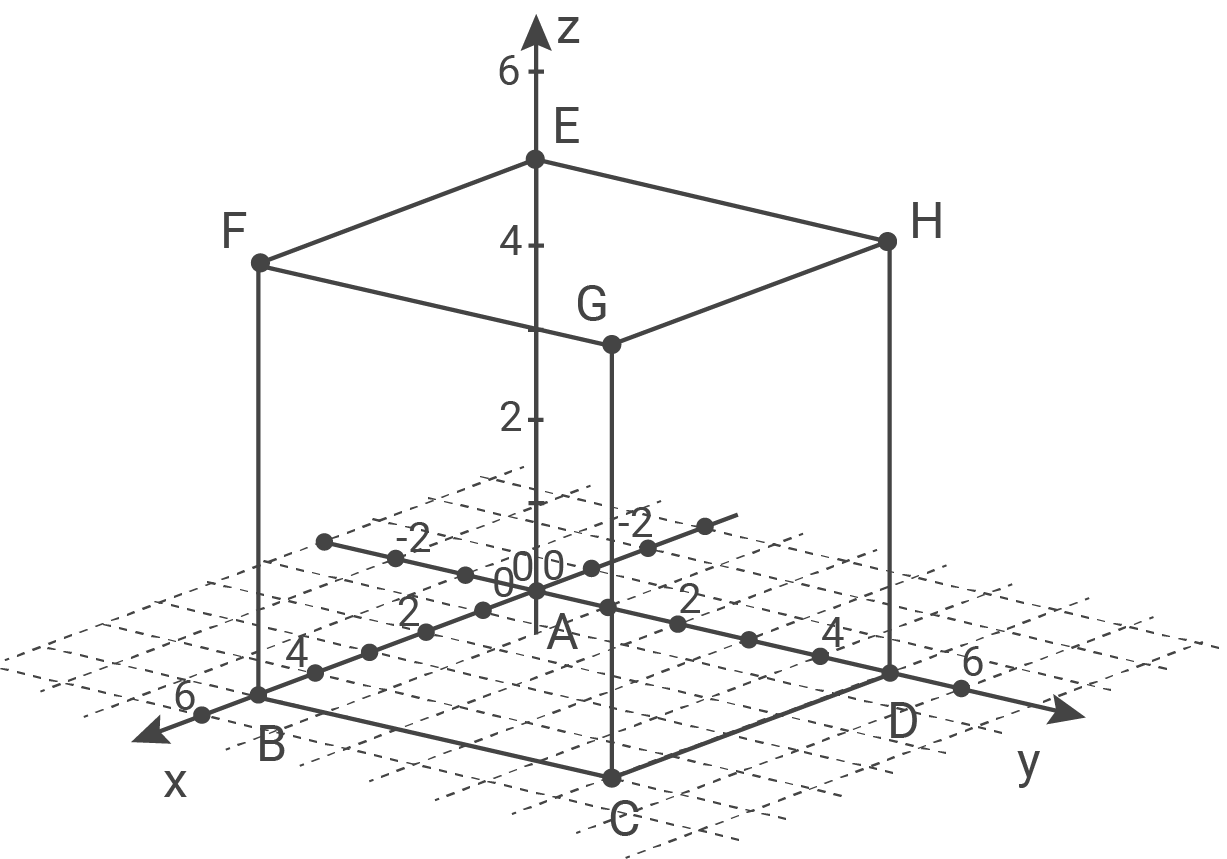
Aufgabe 2 - Analytische Geometrie

Die Abbildung zeigt den Würfel $ABCDEFGH$ mit $G(5\mid 5\mid 5)$ und $H(0\mid 5 \mid 5)$ in einem kartesischen Koordinatensystem. Die Ebene $T$ schneidet die Kanten des Würfels unter anderem in den Punkten $I(5\mid 0 \mid 1),$ $J(2\mid 5\mid 0),$ $K(0\mid 5\mid 2)$ und $L(1\mid 0\mid 5).$

sachsen anhalt abi ea 2019 aufgabe 2 analytische geometrie abbildung 1

a)

Zeichne das Viereck $IJKL$ in die Abbildung ein.

(2 BE)

b)

Begründe, dass das Viereck $IJKL$ ein Trapez ist, in dem zwei gegenüberliegende Seiten gleich lang sind. Weise nach, dass die Seite $\overline{IL}$ des Trapezes doppelt so lang ist wie die Seite $\overline{JK}$ .

(4 BE)

c)

Berechne die Größe eines Innenwinkels des Trapezes $IJKL.$

(2 BE)

d)

Berechne den Flächeninhalt des Trapezes $IJKL.$

(4 BE)

e)

Gegeben ist die Ebene $S:5x+4y+5z=0.$ Der Punkt $K$ liegt in einer Ebene $T,$ die parallel zu $S$ ist. Untersuche, ob auch der Punkt $L$ in $T$ liegt.

(3 BE)

f)

Für einen Wert von $r$ schneidet die Gerade $g:\overrightarrow{x}=\pmatrix{4-r\\0\\r^2+1}+u\cdot \pmatrix{4\\-5\\0}$ mit $u \in \mathbb{R}$ die Kante $\overline{GH}$ des Würfels. Bestimme das Verhältnis, in dem der Schnittpunkt die Kante teilt.

(5 BE)

a)

Abb. 1: Viereck $IJKL$

b)

In der Abbildung von oben kannst du erkennen, dass die beiden parallelen Seiten des Trapezes vermutlich die beiden Seiten $\overline{LI}$ und $\overline{KJ}$ sind. Für die zugehörigen Verbindungsvektoren folgt:

$\begin{array}[t]{rll} \overrightarrow{LI} &=& \pmatrix{4\\0\\-4} \\[5pt] \overrightarrow{KJ} &=& \pmatrix{2\\0\\-2} \end{array}$

Es gilt $\overrightarrow{LI} = 2\cdot \overrightarrow{KJ}.$ Die beiden Vektoren $\overrightarrow{LI}$ und $\overrightarrow{KJ}$ sind also linear abhängig und damit parallel zueinander. Daher sind auch die zugehörigen Vierecksseiten $\overline{LI}$ und $\overline{KJ}$ parallel zueinander. Es handelt sich bei dem Viereck $IJKL$ daher um ein Trapez.
Gefordert ist nun noch zu zeigen, dass die beiden anderen gegenüberliegenden Seiten gleich lang sind. Die Länge der Seiten $\overline{LK}$ und $\overline{IJ}$ kannst du mithilfe des Vektorbetrags berechnen.

$\begin{array}[t]{rll} \overline{LK}&= \sqrt{35} \\[10pt] \overline{IJ}&= \sqrt{35} \\[10pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Es ist also $\overline{LK} = \overline{IJ}.$ Die beiden gegenüberliegenden Seiten $\overline{LK}$ und $\overline{IJ}$ sind also gleich lang. Das Viereck $IJKL$ ist also ein Trapez, bei dem zwei gegenüberliegende Seiten gleich lang sind.

Doppelte Seitenlänge:

Berechne die beiden Längen mithilfe des Vektorbetrags:

$\begin{array}[t]{rll} \overline{IL}&=& \sqrt{32} \\[10pt] \overline{JK} &=& \sqrt{8} \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Vergleiche nun:

$\begin{array}[t]{rll} \overline{IL} &=& \sqrt{32} \\[5pt] &=& \sqrt{8\cdot 4}\\[5pt] &=& \sqrt{8}\cdot \sqrt{4} \\[5pt] &=& 2\cdot \sqrt{8} \\[5pt] &=& 2\cdot \overline{JK} \\[5pt] \end{array}$

Die Strecke $\overline{IL}$ ist also doppelt so lang wie die Strecke $\overline{JK}.$

c)

$\alpha \approx 76,17^{\circ}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Innenwinkel des Trapezes im Punkt $L$ ist ca. $76,17^{\circ}$ groß.

d)

1. Schritt: Höhe des Trapezes berechnen

Die Höhe des Trapezes entspricht dem Abstand der beiden parallelen Seiten $\overline{LI}$ und $\overline{KJ}.$
Diesen kannst du beispielsweise als Abstand des Punktes $K$ zur Gerade durch $L$ und $I$ berechnen.

$LI:\, \overrightarrow{x} = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Um den Abstand von $K$ und $LI$ zu bestimmen, stelle die Gleichung einer Hilfsebene auf, die zu $LI$ senkrecht ist und $K$ enthält. Du kannst also den Richtungsvektor $\overrightarrow{LI} = \pmatrix{4\\0\\-4}$ als Normalenvektor verwenden und erhältst:

$H: \, 4x -4z = d$

Mithilfe einer Punktprobe mit den Koordinaten von $K$ kannst du $d$ berechnen:

$d = -8$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Eine Gleichung der Hilfsebene, die senkrecht zu $LI$ durch $K$ verläuft, lautet:

$H:\, 4x -4z = -8$

Bestimme nun den Schnittpunkt von $H$ und $LI.$ Die Koordinaten der Punkte auf $LI$ lauten $(1+4r \mid 0 \mid 5-4r).$ Einsetzen in die Ebenengleichung von $H$ liefert:

$r= \frac{1}{4}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einsetzen in die Geradengleichung liefert:

$\overrightarrow{OS} = \pmatrix{2\\ 0 \\ 4}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Abstand von $LI$ und $K$ entspricht dem Abstand von $S$ und $K:$

$\overline{SK} = \sqrt{33}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Höhe des Trapezes $IJKL$ beträgt also $\sqrt{33}\,\text{LE}.$

2. Schritt: Flächeninhalt berechnen

Die Längen der beiden parallelen Seiten hast du bereits berechnet. Setze also in die Formel für den Flächeninhalt eines Trapezes ein:

$A\approx 24,37$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Flächeninhalt des Trapezes $IJKL$ beträgt ca. $24,37\,\text{FE}.$

e)

1. Schritt: Ebenengleichung für $T$ aufstellen

Da $T$ parallel zu $S$ verläuft, kannst du einen Normalenvektor von $S$ aus der Ebenengleichung von $S$ ablesen und für $T$ verwenden:

$\overrightarrow{n} = \pmatrix{5\\4\\5}$

Eine Gleichung von $T$ hat also beispielsweise folgende Form:

$T:\, 5x+4y+5z = d$

Da $K$ in dieser Ebene liegen soll, kannst du $d$ über eine Punktprobe mit den Koordinaten von $K$ berechnen:

$d = 30$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Eine Gleichung von $T$ lautet also:

$T:\, 5x+4y+5z = 30$

2. Schritt: Lage des Punkts überprüfen

Setze nun die Koordinaten von $L$ in die Ebenengleichung von $T$ ein, um zu überprüfen, ob $L$ in $T$ liegt:

$30 = 30$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Koordinaten von $L$ erfüllen die Ebenengleichung von $T.$ $L$ liegt also in $T.$

f)

1. Schritt: Geradengleichung aufstellen

$GH:\, \overrightarrow{x} = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

2. Schritt: Schnittpunkt bestimmen

$\pmatrix{5\\5\\5} = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&5&=& 4-r +4u +5s \\ \text{II}\quad&5&=& -5u \\ \text{III}\quad&5&=& r^2 +1 \\ \end{array}$

Aus $\text{II}$ kannst du $u$ berechnen:

$u = -1$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Aus $\text{III}$ kannst du $r$ berechnen:

$\begin{array}[t]{rll} r_1 &=& -2 \\[5pt] r_2 &=& 2 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Setze jetzt beide Lösungen für $r$ in $\text{I}$ ein:

$\begin{array}[t]{rll} \text{I}_1\quad s_1 &=& \frac{3}{5} \\[5pt] \text{I}_2\quad s_2 &=& \frac{7}{5} \\[10pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für $s\leq0$ und $s\geq 1$ liegen die zugehörigen Punkte zwar auf der Geraden $GH,$ allerdings außerhalb der Kante $\overline{GH}.$ Die einzige zulässige Lösung ist also $s_1 = \frac{3}{5}$ mit $r_1 = -2$ und $u=-1.$
Anhand von $s$ kannst du auch das Teilungsverhältnis bestimmen:
$s=0$ beschreibt den Punkt $G,$ $s=1$ beschreibt den Punkt $H.$ Für $0\lt s \lt 1$ werden entsprechend die Punkte zwischen $G$ und $H$ beschrieben. Wegen $s_1 = \frac{3}{5}$ liegt der Schnittpunkt $\frac{3}{5}$ der Strecke $\overline{GH}$ von $G$ und $\frac{2}{5}$ der Strecke $\overline{GH}$ von $H$ entfernt.
Der Schnittpunkt teilt die Kante also im Verhältnis $3:2.$