Aufgabe 1: Analysis

1.1

Die Abbildung 1 zeigt den Graphen $G_f$ der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=\dfrac{1}{80} x^5-\dfrac{1}{6} x^{3}+x .$

Der Punkt $W(2\mid f(2))$ ist ein Wendepunkt von $G_f.$

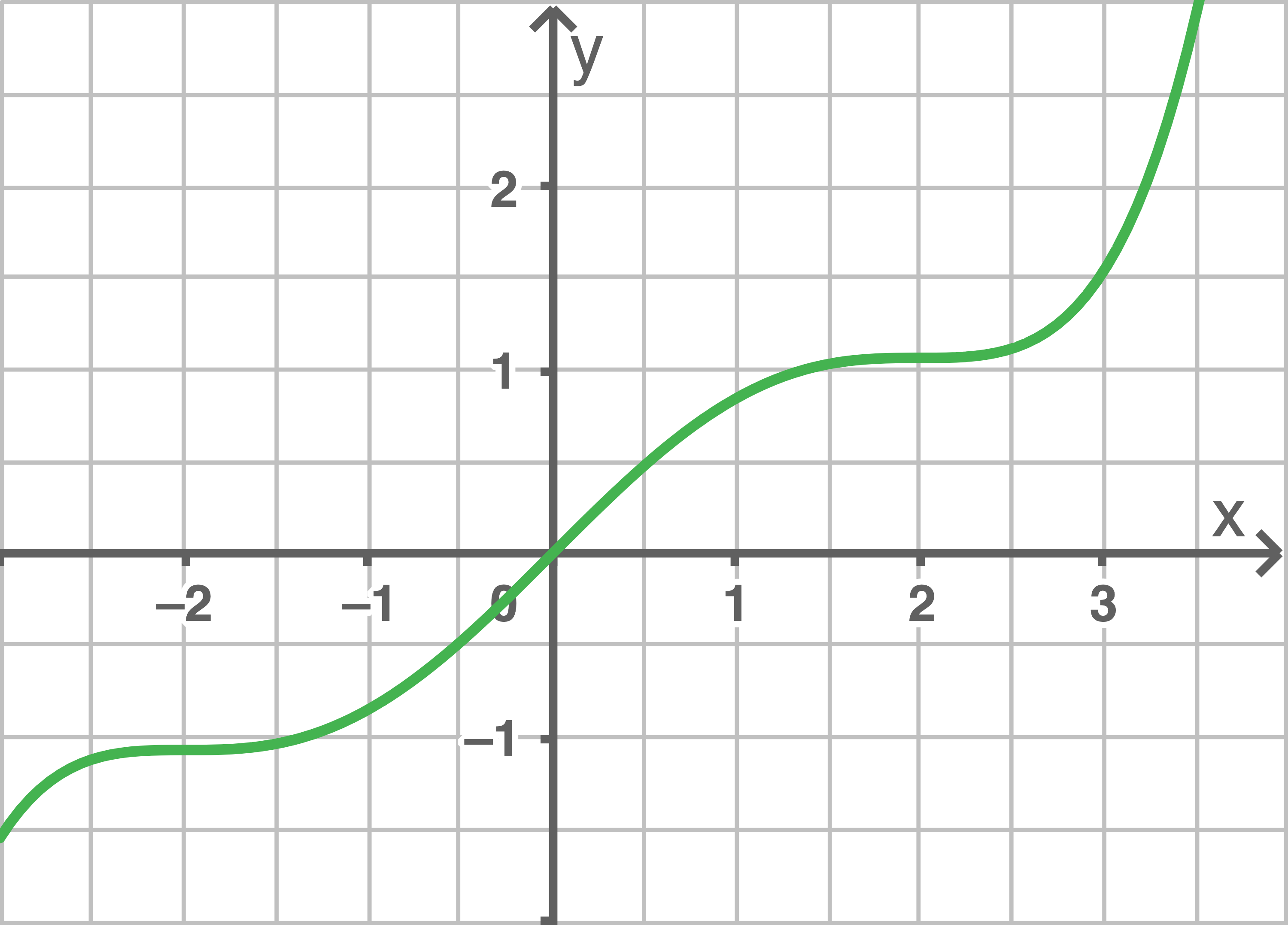
Sachsen-Anhalt Abi 2022 grundlegendes Anforderungsniveau W1

Abbildung 1

Gib die Nullstelle von $f$ an und begründe deine Angabe anhand des Terms von $f.$

(2 BE)

Begründe ohne zu rechnen, dass auch der Punkt $(-2 \mid f(-2))$ ein Wendepunkt von $G_f$ ist.

(2 BE)

Zeige, dass $\(f$ gilt.

(3 BE)

Betrachtet werden die Tangente an $G_f$ im Koordinatenursprung und die Tangente an $G_f$ im Punkt $W.$

Weise nach, dass sich die beiden betrachteten Tangenten im Punkt $\left(\dfrac{16}{15} \bigg\vert \dfrac{16}{15}\right)$ schneiden. Zeichne die beiden Tangenten in die Abbildung 1 ein.

(6 BE)

Begründe geometrisch, dass der Wert des Integrals $\displaystyle\int_{0}^{2}f(x)\;\mathrm dx$ und der Wert des Terms $\dfrac{1}{2} \cdot\left(2+\dfrac{14}{15}\right) \cdot \dfrac{16}{15}$ annähernd übereinstimmen.

(3 BE)

In der Teilaufgabe e) ist der Wert des Integrals $\displaystyle\int_{0}^{2}f(x)\;\mathrm dx$ näherungsweise angegeben. Berechne die prozentuale Abweichung des angegebenen Näherungswerts vom exakten Wert des Integrals.

(5 BE)

Die Funktion $f$ kann im Intervall $[-2 ; 0]$ in guter Näherung durch die Funktion $g$ mit $g(x)=a \cdot\left(x^2-x\right) \cdot \mathrm{e}^x$ und $a \in \mathbb{R}, a \neq 0$ , beschrieben werden. Dabei stimmen die Funktionswerte von $f$ und $g$ an der Stelle $-2$ überein.

Ermittle für $a$ den passenden Wert.

(2 BE)

1.2

Übertöpfe sind Gefäße, in die Pflanztöpfe gestellt werden können.

Betrachtet werden rotationssymmetrische Übertöpfe mit einer kreisförmigen Grundfläche und einer Höhe von $40 \,\text{cm}$ .

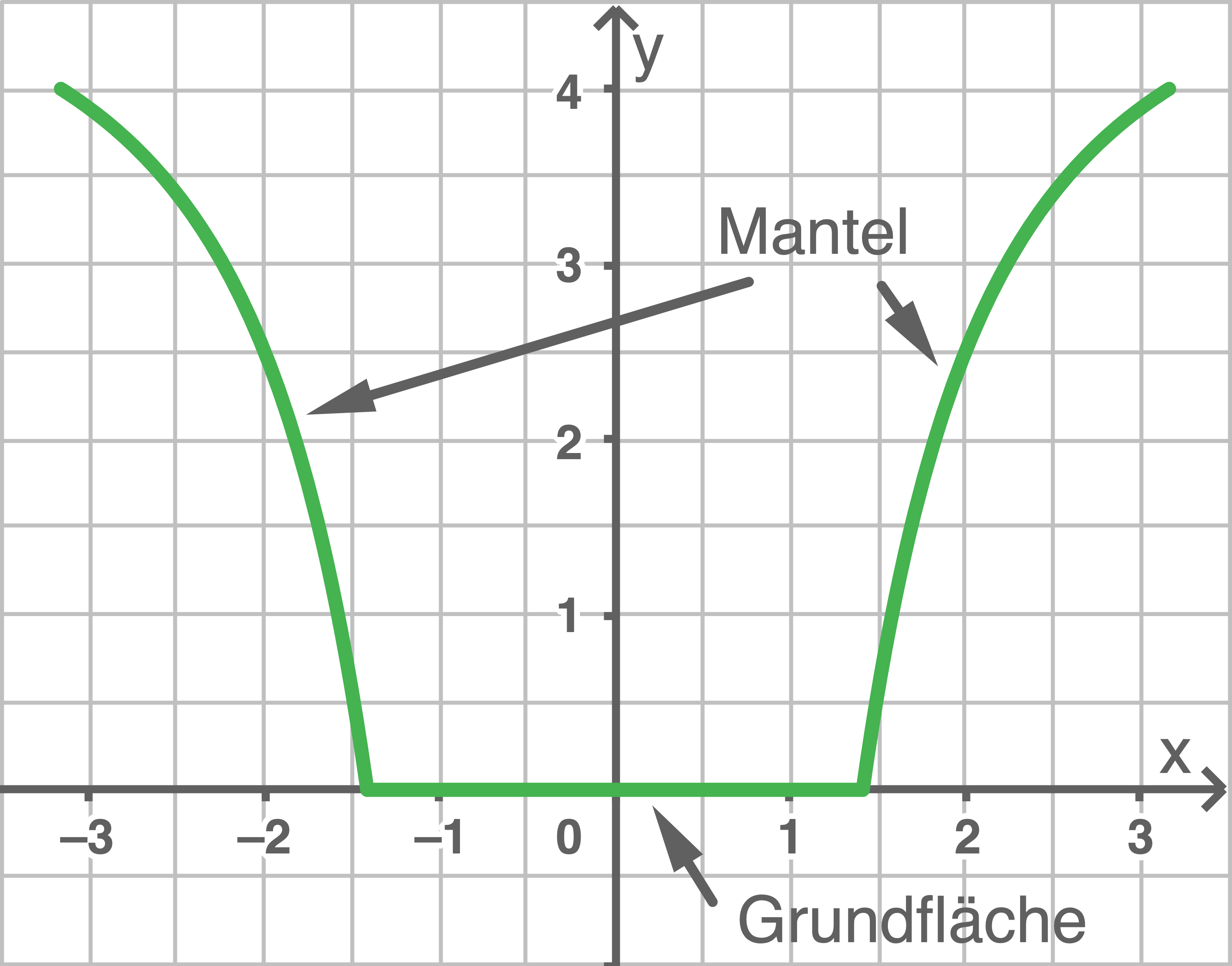
Die Abbildung 2 zeigt für einen solchen Übertopf die Profillinie eines Längsschnitts entlang der Rotationsachse des Übertopfs. Die Rotationsachse wird durch die $y$ -Achse dargestellt.

Die Profillinie des Mantels kann mithilfe der Funktion $h$

mit $h(x)=5-\dfrac{10}{x^2} \quad x \in \mathbb{R}, x \neq 0,$

beschrieben werden.

Eine Längeneinheit im Koordinatensystem entspricht $10\,\text{cm}$ in der Realität.

Sachsen-Anhalt Abi 2022 grundlegendes Anforderungsniveau Topf

Abbildung 2

Zeige rechnerisch für den in der Abbildung 2 dargestellten Übertopf, dass die Grundfläche einen Durchmesser von etwa $28\,\text{cm}$ hat.

(3 BE)

Untersuche, ob ein zylinderförmiger Pflanztopf mit einem Durchmesser von $24\,\text{cm}$ und einem Volumen von $16$ Litern in den in der Abbildung 2 dargestellten Übertopf hineinpasst, ohne über den oberen Rand des Übertopfs hinauszuragen.

(4 BE)

Für jeden der betrachteten Übertöpfe kann - in einem Längsschnitt entlang der Rotationsachse des Übertopfs - die Profillinie des Mantels mithilfe einer der Funktionen $h_k$ mit $h_k(x)=k-\dfrac{10}{x^2},$ $\: x \in \mathbb{R}, \: x \neq 0, \: k \in \mathbb{R}, \, k\gt 4$ , beschrieben werden.

Berechne denjenigen Wert von $k$ , für den der Radius des oberen Rands des Übertopfs doppelt so groß ist wie der Radius seiner Grundfläche.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$f(x)=0$

$\dfrac{1}{80}x^5-\dfrac{1}{6}x^3+x=0$

$x\left(\dfrac{1}{80}x^4-\dfrac{1}{6}x^2+1\right)=0$

Wegen des Satzes vom Nullprodukt folgt $x=0.$

Der Graph von $G_f$ ist punktsymmetrisch zum Ursprung. Da $W(2\mid f(2))$ ein Wendepunkt von $G_f$ ist, folgt daraus, dass auch der Punkt $(-2\mid f(-2))$ eine Wendepunkt von $G_f$ ist.

$f(x)=\dfrac{1}{80}x^5-\dfrac{1}{6}x^3+x$

$\(f$ $=\dfrac{1}{16}x^4-\dfrac{1}{2}x^2+1$

Dass $\(f$ diesen Funktionsterm hat, ist nun zu zeigen:

$\(f$ $=\dfrac{1}{16}\cdot \left(x^2-4\right)^2$ $=\dfrac{1}{16}\cdot \left(x^4-8x^2+16\right)$ $=\dfrac{1}{16}x^4-\dfrac{1}{2}x^2+1$

1. Schritt: Tangentengleichung $t_1$ aufstellen

$t_1:y=m_1x+b_1$

$\(m_1=f$

Die Tangente verläuft durch den Koordinatenursprung und hat somit die Gleichung $t_1:y=x$

2. Schritt: Tangentengleichung $t_2$ aufstellen

$t_2:y=m_2x+b_2$

$\(m_2=f$

$f(2)=\dfrac{1}{80}\cdot 2^5-\dfrac{1}{6}\cdot 2^3+2$ $=\dfrac{32}{80}-\dfrac{8}{6}+2$ $=\dfrac{16}{15}$

$t_2:y=\dfrac{16}{15}$

3. Schritt: Schnittpunkt berechnen

$t_1(x)=t_2(x)$

$x=\dfrac{16}{15}$

$x=\dfrac{16}{15}$ in $t_1$ ergibt $y=\dfrac{16}{15}.$

Also ist gezeigt, dass sich die Tangenten im Punkt $\left(\dfrac{16}{15}\bigg\vert\dfrac{16}{15}\right)$ schneiden.

Der Graph der Funktion $f$ und die $x$ -Achse schließen im Intervall $[0;2]$ circa 6 Kästchen ein. Dies entspricht einer Fläche von $0,5 \cdot 0,5 \cdot 6 \cdot = 1,5 \;\text{[FE]}$ und somit ungefähr dem Wert des Integrals.

$\dfrac{1}{2}\cdot \left(2+\dfrac{14}{15}\right)\cdot \dfrac{16}{15}\approx 1,56$ ist ein Näherungswert und stimmt somit annähernd mit dem Wert des Flächeninhalts überein.

Näherungswert: $\dfrac{1}{2}\cdot \left(2+\dfrac{14}{15}\right)\cdot \dfrac{16}{15}\approx 1,56$

Exakter Wert:

$\displaystyle\int_{0}^{2}f(x)\;\mathrm dx$ $=\displaystyle\int_{0}^{2}\left(\dfrac{1}{80}x^5-\dfrac{1}{6}x^3+x\right)\;\mathrm dx$ $=\left[\dfrac{1}{480}x^6-\dfrac{1}{24}x^4+\dfrac{1}{2}x^2\right]_0^2$ $=\left(\dfrac{64}{480}-\dfrac{16}{24}+\dfrac{4}{2}\right)-0$ $\approx 1,47$

Prozentuale Abweichung:

$\dfrac{1,56}{1,47}\approx 1,06,$ also $6\,\%$ Abweichung

$f(-2)=g(-2)$

$\dfrac{1}{80}\cdot(-2)^5-\dfrac{1}{6}\cdot (-2)^3-2=a\cdot ((-2)^2-(-2))\cdot \mathrm e^{-2}$

$-\dfrac{16}{15}=\dfrac{6a}{\mathrm e^2}$

$a=-\dfrac{8}{45}\mathrm e^2$

1.2

Nullstellen von $h(x)$ berechnen:

$h(x)=0$

$\begin{array}[t]{rll} 5-\dfrac{10}{x^2}&=&0 &\scriptsize \mid\;+\dfrac{10}{x^2}\\[5pt] 5&=&\dfrac{10}{x^2}&\scriptsize \mid\;\cdot x^2\;\mid:5\\[5pt] x^2&=&2 \end{array}$