Aufgabe 1 - Analysis
Die Abbildung 1 zeigt den Graphen der Funktion 
mit 
und 
.
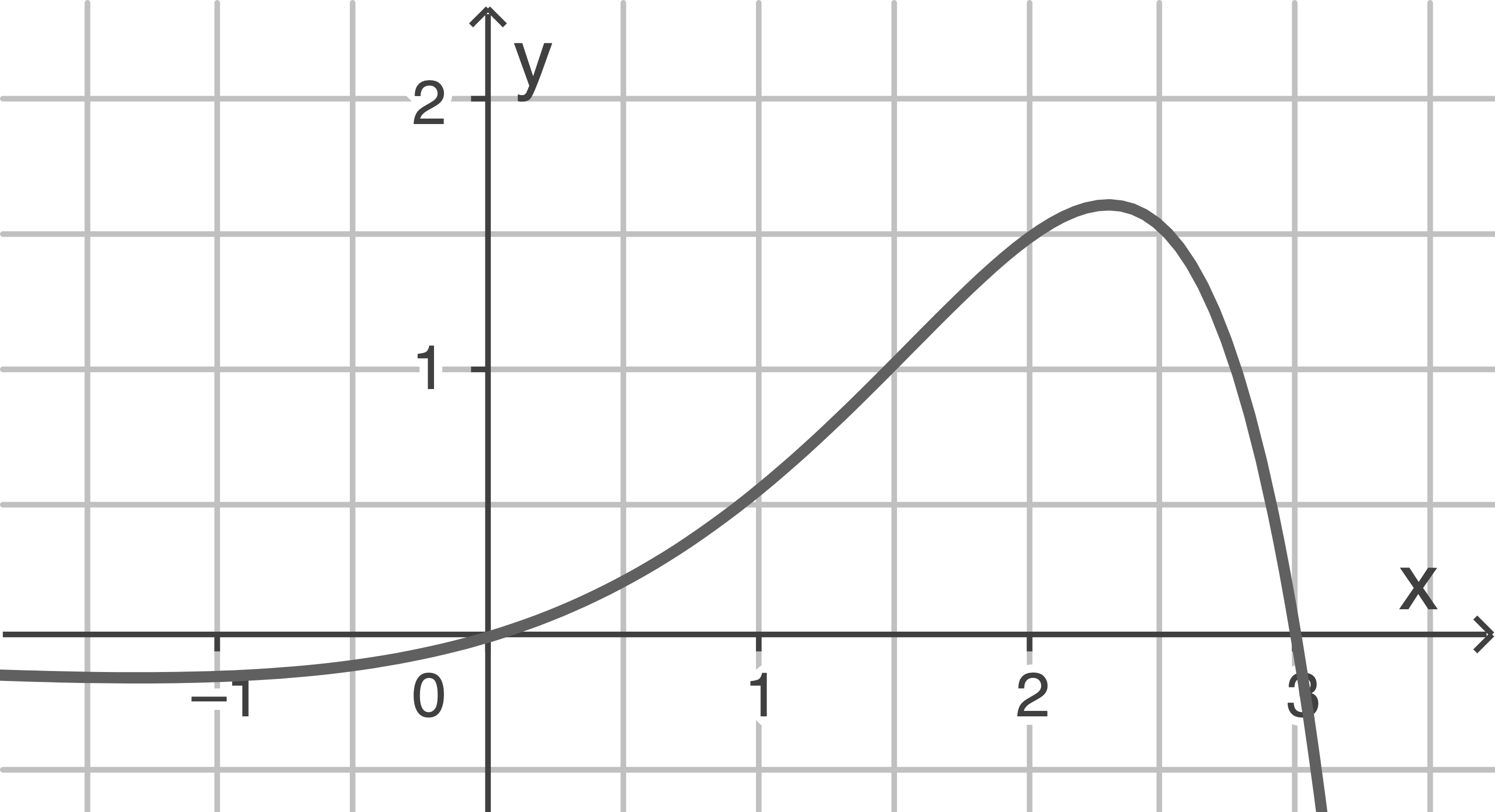
Abbildung 1
1.1
Für die erste Ableitungsfunktion 
von gilt 
a)
Gib die Nullstellen von an und berechne die 
-Koordinate des Hochpunkts des Graphen von .
3 BE
b)
Eine der Tangenten an den Graphen von verläuft durch den Punkt 
Zeichne diese Tangente in die Abbildung ein und gib eine Gleichung der eingezeichneten Gerade an.
3 BE
c)
Berechne die Größe des Steigungswinkels des Graphen von im Koordinatenursprung.
2 BE
d)
Zeige, dass die in 
definierte Funktion 
mit 
eine Stammfunktion von ist.
4 BE
e)
Deute das Integral 
geometrisch und berechne seinen Wert.
3 BE
f)
Begründe, ohne zu rechnen, dass es eine positive Zahl 
gibt, für die 
gilt.
3 BE
g)
Begründe ohne Verwendung des Funktionsterms von , dass der Graph jeder Stammfunktion von einen Tiefpunkt hat, der auf der 
-Achse liegt.
3 BE
1.2
Für jeden Wert von 
ist eine Funktion 
mit 
und 
gegeben.
Für die erste Ableitungsfunktion von gilt 
Die folgende Abbildung zeigt die Graphen von
und 
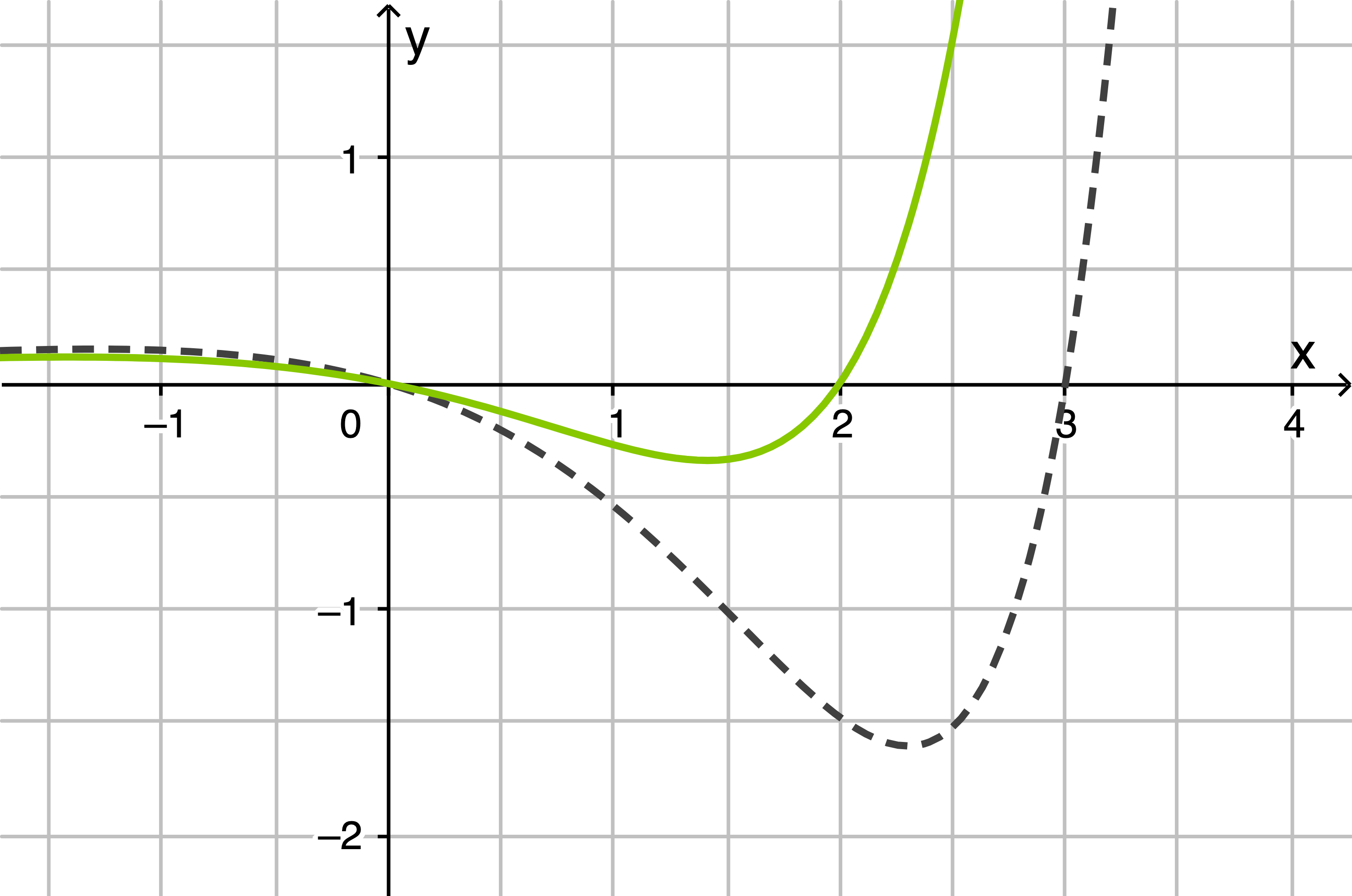
Für die erste Ableitungsfunktion von
Die folgende Abbildung zeigt die Graphen von
a)
Bestimme denjenigen Wert von 
für den der Graph von und der Graph von eine Figur begrenzen, die bezüglich der -Achse symmetrisch ist.
2 BE
b)
Für jeden Wert von 
haben die Graphen von und 
einen gemeinsamen Punkt. Berechne die x-Koordinate dieses Punkts.
3 BE
c)
Für jeden Wert von schließen die Graphen von und 
im vierten Quadranten mit der -Achse ein Flächenstück ein.
Markiere dieses Flächenstück für 
in der obigen Abbildung.
Für einen Wert von beträgt der Inhalt des Flächenstücks 
gib eine Gleichung an, mit der dieser Wert von bestimmt werden könnte.
4 BE
1.1
a)
Nullstellen von f:
![\(\begin{array}[t]{rll}
f(x) &=& 0 \\[5pt]
\frac{1}{10}\cdot x \cdot (3-x) \cdot \mathrm e^x &=& 0 &\quad \scriptsize \mid\; :\mathrm e^x \neq 0 \\[5pt]
\frac{1}{10}\cdot x \cdot (3-x) &=& 0 &\quad \scriptsize \mid\; :\frac{1}{10}\\[5pt]
x \cdot (3-x) &=& 0 &\quad \scriptsize \mid\;x_1 = 0 \\[5pt]
3-x &=& 0 &\quad \scriptsize \mid\; +x \\[5pt]
3 &=& x_2
\end{array}\)](https://mathjax.schullv.de/a026e04b06e62b062ae4b88a73f50e65301acc26664956fb7466aa5dd2296f65?color=5a5a5a)
Die Nullstellen von sind 
und 
x-Koordinate des Hochpunktes:
Wende das notwendige Kriterium für Extremstellen von f an:
Mithilfe der Abbildung auf dem Aufgabenblatt ergibt sich die x-Koordinate des Hochpunktes des Graphen von zu 
Vollständige Lösung anzeigen
b)
c)
Der Steigungswinkel im Koordinatenursprung lässt sich über die Steigung des Graphen von an der Stelle 
berechnen:
![\(\begin{array}[t]{rll}
m &=& f](https://mathjax.schullv.de/fa2c74db2a385b13cbb74e39c3c85bf500628b8382defc1d353320165f6f8469?color=5a5a5a)
Für den Steigungswinkel 
folgt:
![\(\begin{array}[t]{rll}
\alpha &=& \tan^{-1}(m) \\[5pt]
&=& \tan^{-1}(0,3) \\[5pt]
&\approx& 16,70^{\circ}
\end{array}\)](https://mathjax.schullv.de/e023e4a9a6eaf0e3be7d08da8296c8e83b589e1b64150d1f61ab735d8cfec68d?color=5a5a5a)
Der Steigungswinkel des Graphen von im Koordinatenursprung beträgt ca. 
d)
e)
Das Integral beschreibt den Inhalt der Fläche, die der Graph von mit der -Achse im Bereich 
einschließt.
f)
Betrachtet wird ein Wert 
dann gilt:
Das Integral 
beschreibt den Flächeninhalt der Fläche, die der Graph von im Bereich 
mit der -Achse begrenzt.
Diese Fläche liegt allerdings unterhalb der-Achse, wodurch der Wert des Integrals negativ ist. Je größer der Wert von gewählt wird, desto größer wird die Fläche und desto größer wird der Betrag des Integralwerts.
Es gibt also definitiv einen Wert von
für den der Betrag dieses Integrals genauso groß ist, wie der Betrag des ersten Intregrals, sodass der Gesamtwert 
beträgt.
Diese Fläche liegt allerdings unterhalb der
Es gibt also definitiv einen Wert von
g)
An der Stelle
Damit besitzt der Graph jeder Stammfunktion
1.2
a)
Der Graph von muss der Spiegelung des Graphen von an der -Achse entsprechen.
Für den Funktionsterm bedeutet das:
Dies ist für 
erfüllt. Für begrenzen der Graph von und der Graph von also eine Figur, die bezüglich der -Achse symmetrisch ist.
Für den Funktionsterm bedeutet das:
b)
c)
