Pflichtaufgaben
1.
Gegeben sind die in  definierten Funktionen
definierten Funktionen  mit
mit  und
und  Der Graph von
Der Graph von  entsteht durch Verschieben des Graphen von
entsteht durch Verschieben des Graphen von  um zwei Einheiten entlang der
um zwei Einheiten entlang der  -Achse nach rechts.
-Achse nach rechts.
a)
Gib die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse an.
-Achse an.
(1 BE)
b)
Gib einen Funktionsterm für  an.
an.
(1 BE)
c)
Begründe, dass die Graphen der Ableitungsfunktionen von  und
und  keinen Punkt gemeinsam haben.
keinen Punkt gemeinsam haben.
(3 BE)
2.
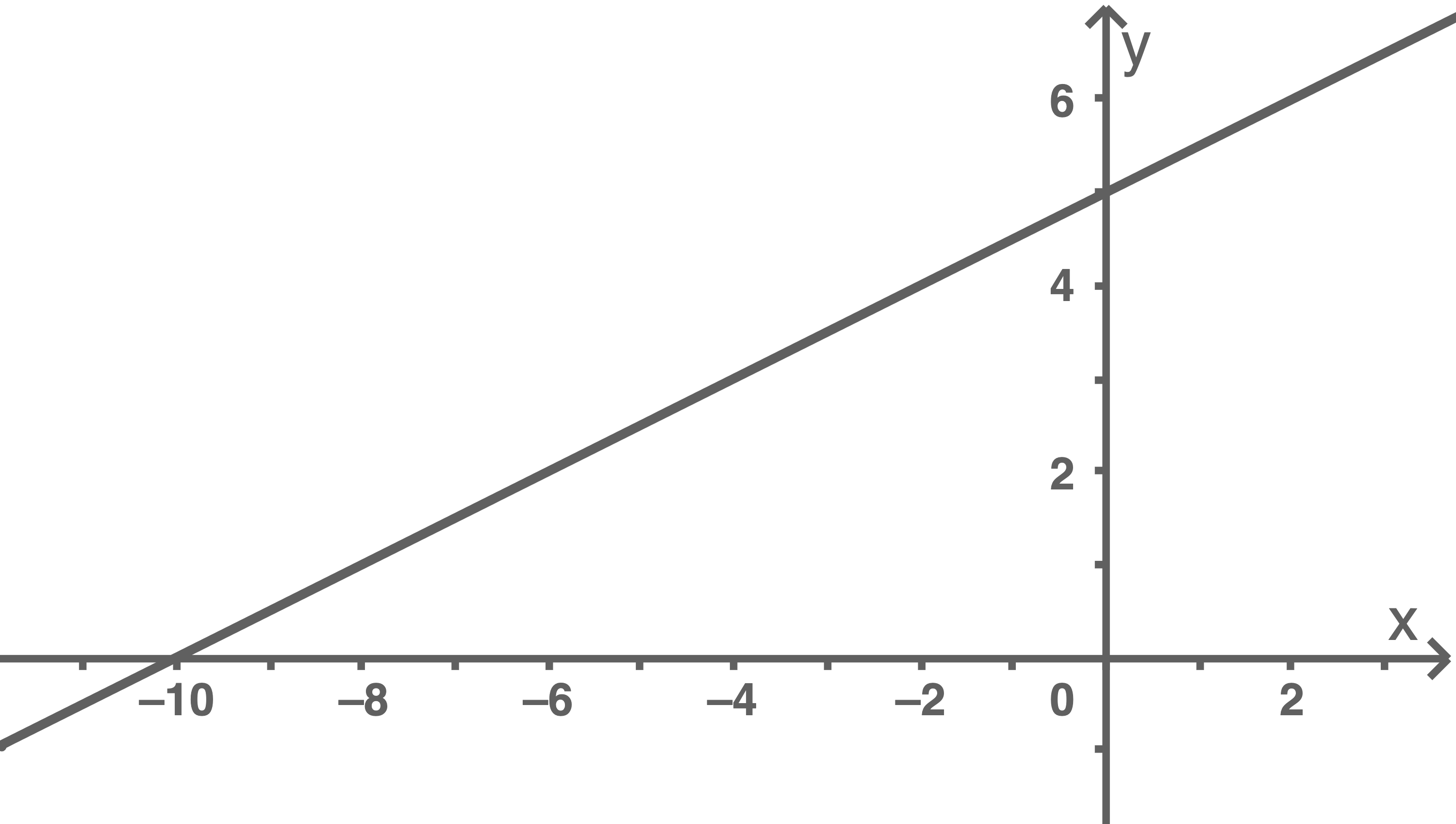
Die Abbildung zeigt den Graphen der in  definierten linearen Funktion
definierten linearen Funktion 
a)
Begründe, dass  gilt.
gilt.
(1 BE)
b)
Berechne den Abstand des Koordinatenursprungs zum Graphen.
(4 BE)
3.
Gegeben sind die Gerade  mit
mit  sowie die Gerade
sowie die Gerade  durch die Punkte
durch die Punkte  und
und  mit einer reellen Zahl
mit einer reellen Zahl 
a)
Begründe, dass  nicht auf
nicht auf  liegt.
liegt.
(1 BE)
b)
Die Geraden  und
und  haben einen gemeinsamen Punkt.
Ermittle den Wert von
haben einen gemeinsamen Punkt.
Ermittle den Wert von 
(4 BE)
4.
Die Abbildung zeigt ein Baumdiagramm zu einem zweistufigen Zufallsexperiment mit den Ereignissen  und
und  Es gilt:
Es gilt:  und
und 
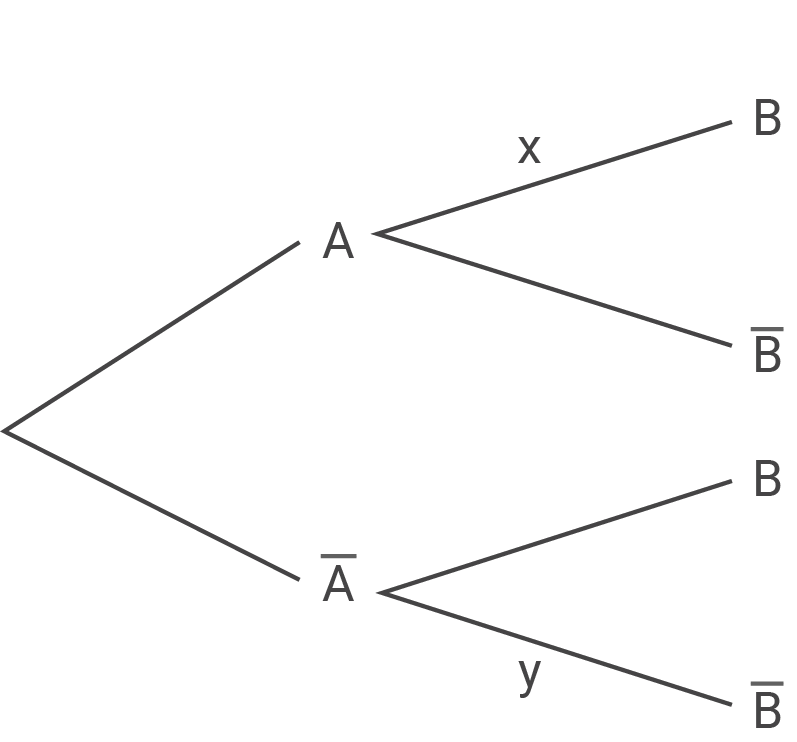
a)
Bestimme die Werte von  und
und  und weise nach, dass
und weise nach, dass  gilt.
gilt.
(3 BE)
b)
Berechne 
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Für den Schnittpunkt mit der  -Achse gilt
-Achse gilt  Somit folgt:
Somit folgt:
 Der Schnittpunkt mit der
Der Schnittpunkt mit der  -Achse besitzt somit die Koordinaten
-Achse besitzt somit die Koordinaten 
b)
c)
2.
a)
Die Steigung der Geraden lässt sich durch ein Steigungsdreieck bestimmen. Hierfür können die Schnittpunkte mit den Koordinatenachsen abgelesen werden:  und
und  Die Steigung folgt nun mit
Die Steigung folgt nun mit  Aufgrund des
Aufgrund des  -Achsenabschnitts folgt
-Achsenabschnitts folgt 
b)
1. Schritt: Lotgerade  aufstellen
Da die Lotgerade senkrecht zum Graphen von
aufstellen
Da die Lotgerade senkrecht zum Graphen von  stehen soll, ergibt sich:
stehen soll, ergibt sich:
 Die Lotgerade soll durch den Ursprung verlaufen. Einsetzen in die allgemeine Geradengleichung liefert also:
Die Lotgerade soll durch den Ursprung verlaufen. Einsetzen in die allgemeine Geradengleichung liefert also:
![\(\begin{array}[t]{rll}
0&=& -2\cdot 0+c& \\[5pt]
0&=& c
\end{array}\)](https://mathjax.schullv.de/9d4be1bb07035d74f4c061409629bb8c4e4534d50f5465c9ea0d5dc2ff3358ec?color=5a5a5a) 2. Schritt: Schnittpunkt bestimmen
2. Schritt: Schnittpunkt bestimmen
![\(\begin{array}[t]{rll}
f(x)&=& g(x)& \\[5pt]
\dfrac{1}{2}\cdot x+5&=& -2\cdot x &\quad \scriptsize \mid\; +2x \quad \scriptsize \mid\;-5 \\[5pt]
\dfrac{5}{2}x&=& -5&\quad \scriptsize \mid\; \cdot \dfrac{2}{5}\\[5pt]
x&=& -2
\end{array}\)](https://mathjax.schullv.de/a89822adb25f0dd3a06829a87360ee1b5b8e562b039c20910b47e62fac990dc2?color=5a5a5a)
 -Koordinate ermitteln:
-Koordinate ermitteln:
 Der Schnittpunkt des Graphen von
Der Schnittpunkt des Graphen von  mit der Lotgeraden besitzt somit die Koordinaten
mit der Lotgeraden besitzt somit die Koordinaten  3. Schritt: Abstand berechnen
Der Abstand des Koordinatenursprungs zum Graphen von
3. Schritt: Abstand berechnen
Der Abstand des Koordinatenursprungs zum Graphen von  entspricht dem Abstand der Punkte
entspricht dem Abstand der Punkte  und
und  Es ergibt sich also:
Es ergibt sich also:
![\(\begin{array}[t]{rll}
d(O,S)&=& \left| \sqrt{(0-(-2))^2+(0-4)^2} \right| & \\[5pt]
&=& \left| \sqrt{20} \right| & \\[5pt]
&\approx& 4,47 \; [\text{LE}]
\end{array}\)](https://mathjax.schullv.de/b2cab5a7b8468ddd0ac3a91dba4331c9433459878b8b6c88cf5603da37c77a70?color=5a5a5a)
3.
a)
Einsetzen des Ortsvektors von  in
in  liefert:
liefert:
 Aus der zweiten Zeile ergibt sich unabhängig von
Aus der zweiten Zeile ergibt sich unabhängig von  der Widerspruch
der Widerspruch  Somit liegt
Somit liegt  nicht auf
nicht auf 
b)
1. Schritt: Gleichung von  aufstellen
aufstellen
![\(\begin{array}[t]{rll}
h: \overrightarrow{x}&=&\overrightarrow{OA}+t\cdot \overrightarrow{AB} &\\[5pt]
&=&\pmatrix{4\\0\\0}+t\cdot \pmatrix{1\\1\\b}
\end{array}\)](https://mathjax.schullv.de/5d37cc2de0b135df136d4102c0ebd6d7ac64d74215c4f496f38bbd605b497122?color=5a5a5a) 2. Schritt: Schnittpunkt bestimmen
Gleichsetzen der Geradengleichungen liefert:
2. Schritt: Schnittpunkt bestimmen
Gleichsetzen der Geradengleichungen liefert:
 Aus der 2. Zeile ergibt sich
Aus der 2. Zeile ergibt sich  Einsetzen in die 1. Zeile liefert:
Einsetzen in die 1. Zeile liefert:
![\(\begin{array}[t]{rll}
2+s&=& 4+3&\quad \scriptsize \mid\; -2\\[5pt]
s&=& 5
\end{array}\)](https://mathjax.schullv.de/4e745c29e59210adb077cc4067e7cb8dc1117221a35c676f2fd3b87dbfbc9730?color=5a5a5a) Aus der 3. Zeile folgt nun:
Aus der 3. Zeile folgt nun:
![\(\begin{array}[t]{rll}
-7+5\cdot 5&=& 3\cdot b& \\[5pt]
18&=& 3\cdot b&\quad \scriptsize \mid\; :3 \\[5pt]
6&=& b
\end{array}\)](https://mathjax.schullv.de/b55a239bc18c33520404608cc3bea2c5f00fcfdd4087ceff55048a63b3371889?color=5a5a5a)
4.
a)
Wegen  folgt
folgt  Außerdem gilt:
Außerdem gilt:  Der Wert von
Der Wert von  lässt sich wie folgt bestimmen:
lässt sich wie folgt bestimmen:
![\(\begin{array}[t]{rll}
P(\overline{A}\cap\overline{B})&=& 0,56& \\[5pt]
P(\overline{A})\cdot P_A(\overline{B})&=& 0,56& \\[5pt]
0,8\cdot y&=& 0,56& \quad \scriptsize \mid :0,8\\[5pt]
y&=& 0,7
\end{array}\)](https://mathjax.schullv.de/3e05c827755334f7f6c5135ecdaeaf0fd9aeff883b5411ef5598da23e11aa7b2?color=5a5a5a) Für den Wert von
Für den Wert von  gilt also:
gilt also:
![\(\begin{array}[t]{rll}
P(B)&=& P(A\cap B)+P(\overline{A}\cap B) & \\[5pt]
&=& P(A)\cdot P_A(B)+P(\overline{A})\cdot P_{\overline{A}}(B)& \\[5pt]
&=& P(A)\cdot x+P(\overline{A})\cdot (1-y) & \\[5pt]
&=& 0,2\cdot 0,8+0,8\cdot 0,3 & \\[5pt]
&=& 0,16 + 0,24 & \\[5pt]
&=& 0,4
\end{array}\)](https://mathjax.schullv.de/c78ae79b0b3228e62b225ccc60f66682dbd86ed93107a56b6e86fef63cda63a5?color=5a5a5a)
b)
Mit dem Satz von Bayes ergibt sich:
![\(\begin{array}[t]{rll}
P_B(A)&=& \dfrac{P_A(B)\cdot P(A)}{P(B)}& \\[5pt]
&=& \dfrac{0,8\cdot 0,2}{0,4}& \\[5pt]
&=& 0,4
\end{array}\)](https://mathjax.schullv.de/37c7a7588fdd9b416d3d616f3604db05a94eb54d5ca51426920a933c0ddf81b2?color=5a5a5a)