Wahlpflichtaufgaben (Aufgabengruppe 1)
4.1
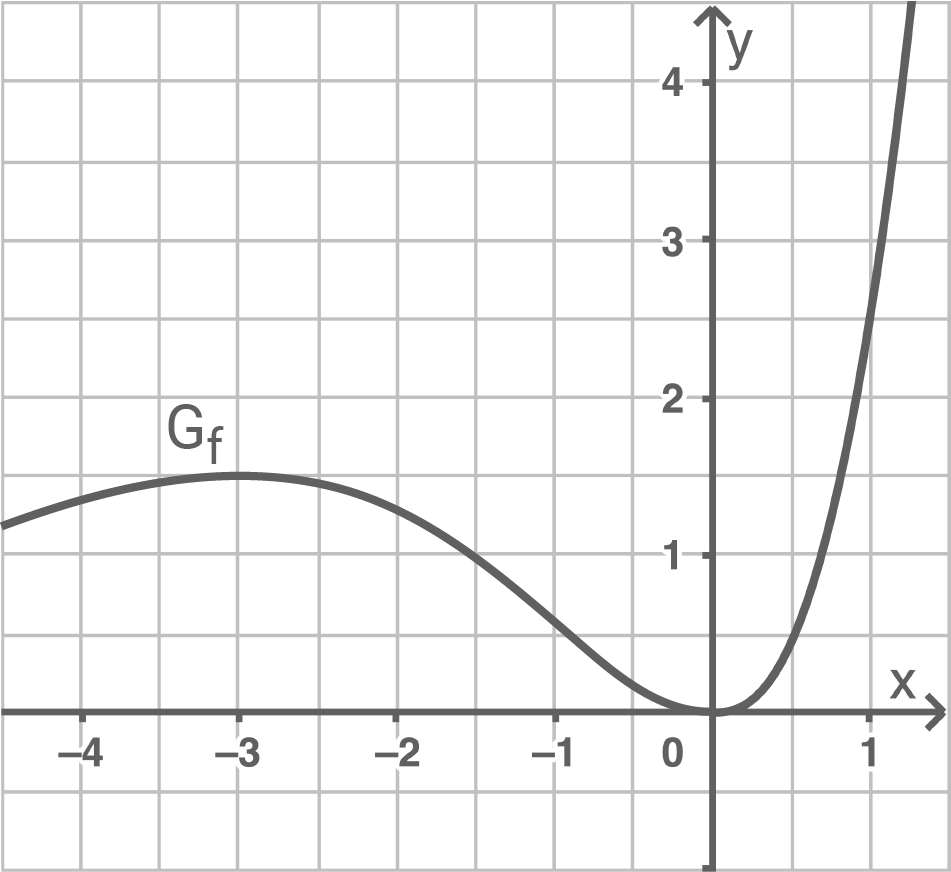
Die Abbildung zeigt den Graphen  einer in
einer in  definierten Funktion
definierten Funktion 

a)
Bestimme grafisch den Wert des Integrals 
(2 BE)
b)
Beschreibe, wie der Graph der in  definierten Funktion
definierten Funktion  mit
mit  aus
aus  erzeugt werden kann.
Gib die Koordinaten des Hochpunkts des Graphen von
erzeugt werden kann.
Gib die Koordinaten des Hochpunkts des Graphen von  an.
an.
(3 BE)
4.2
Die Punkte 

 und
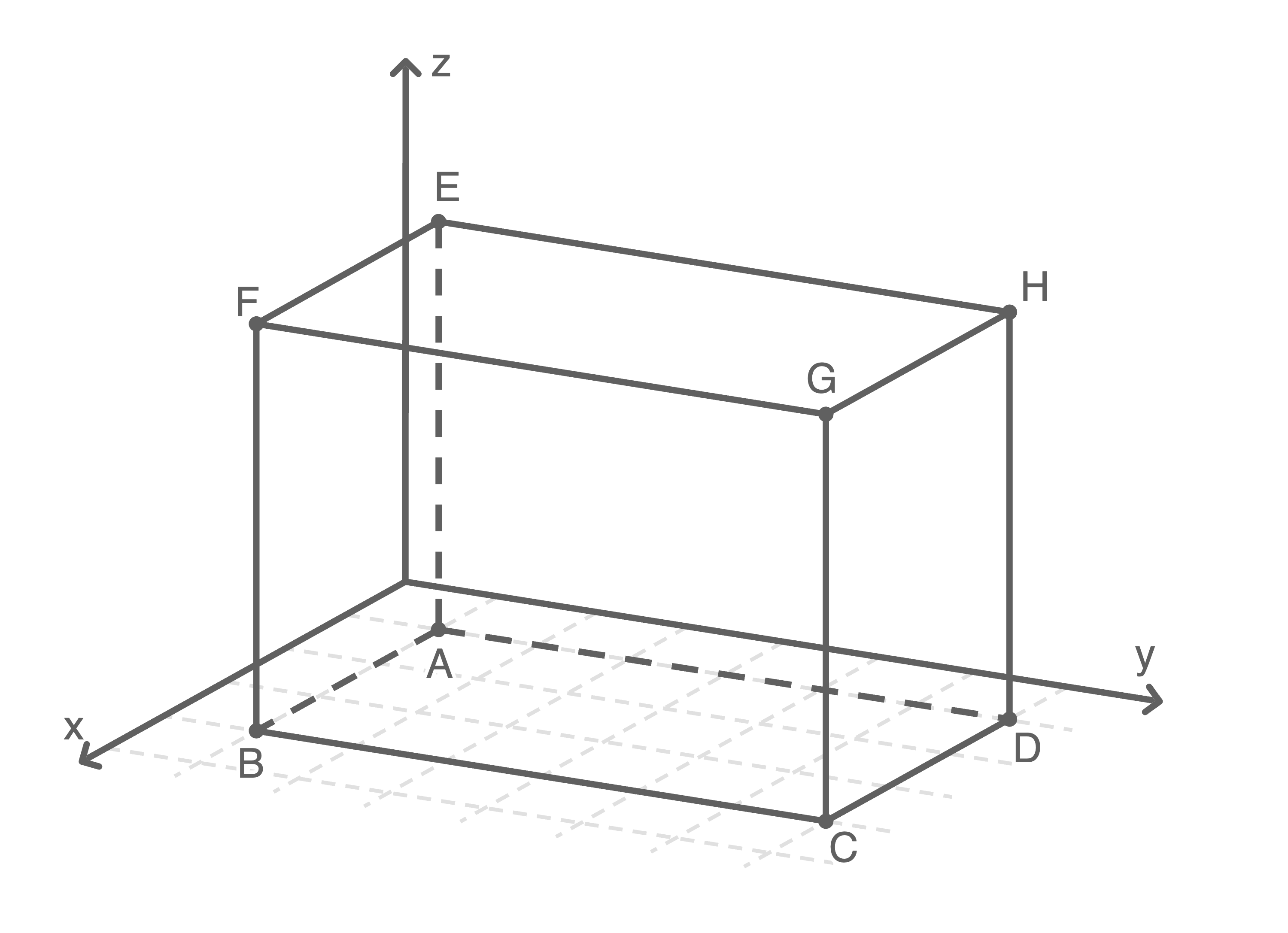
und  sind Eckpunkte des in der Abbildung dargestellten Quaders
sind Eckpunkte des in der Abbildung dargestellten Quaders 

a)
Gib die Koordinaten des Punktes  an.
an.
(1 BE)
b)
Der Quader wird parallel zu einer Gerade so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen im Koordinatenursprung befindet. Dabei entsteht der Quader  Ermittle die Koordinaten des Punkts
Ermittle die Koordinaten des Punkts 
(3 BE)
c)
Gib einen Eckpunkt des Quaders  an, der nur positive Koordinaten hat.
an, der nur positive Koordinaten hat.
(1 BE)
4.3
Auf einer Spendengala wird das folgende Spiel angeboten:
Für einen Einsatz von 3 Euro dreht der Spieler zweimal ein Glücksrad. Dieses besteht aus mehreren gleich großen Sektoren.
 der Sektoren sind grün eingefärbt. Für jedes Erzielen eines grünen Sektors werden dem Spieler 10 Euro ausgezahlt.
der Sektoren sind grün eingefärbt. Für jedes Erzielen eines grünen Sektors werden dem Spieler 10 Euro ausgezahlt.
a)
Zeige, dass die Wahrscheinlichkeit dafür, bei diesem Spiel genau einmal einen grünen Sektor zu erzielen,  beträgt.
beträgt.
(2 BE)
b)
Begründe, dass der Veranstalter der Spendengala erwarten kann, mit diesem Spiel auf lange Sicht mehr Geld einzunehmen als auszuzahlen.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
4.1
a)
Der Wert des Integrals gibt den Inhalt der Fläche zwischen dem Graphen und der  -Achse zwischen den beiden Grenzen an. Im betrachteten Bereich sind das ungefähr 8 Kästchen, das heißt der Wert des Integrals ist etwa
-Achse zwischen den beiden Grenzen an. Im betrachteten Bereich sind das ungefähr 8 Kästchen, das heißt der Wert des Integrals ist etwa ![\(8\cdot0,5^2=2\;[\text{FE}].\)](https://mathjax.schullv.de/f52af0e22124d1ded4d66412fc64dfb022b2971fc07ebf226bf4f3e0663bc090?color=5a5a5a)
b)
Der Graph der Funktion  geht durch Spiegelung an der
geht durch Spiegelung an der  -Achse und Verschiebung um 2 Einheiten in positive
-Achse und Verschiebung um 2 Einheiten in positive  -Richtung aus dem Graphen
-Richtung aus dem Graphen  hervor.
Aus der Abbildung können die Koordinaten des Tiefpunkts von
hervor.
Aus der Abbildung können die Koordinaten des Tiefpunkts von  mit
mit  abgelesen werden.
Da der Graph
abgelesen werden.
Da der Graph  und somit auch sein Hochpunkt und Tiefpunkt an der
und somit auch sein Hochpunkt und Tiefpunkt an der  -Achse gespiegelt wird, entspricht der Tiefpunkt des Graphen von
-Achse gespiegelt wird, entspricht der Tiefpunkt des Graphen von  dem Hochpunkt des Graphen von
dem Hochpunkt des Graphen von  vor der Verschiebung in
vor der Verschiebung in  -Richtung.
Verschieben um 2 Einheiten in positive
-Richtung.
Verschieben um 2 Einheiten in positive  -Richtung liefert dann:
-Richtung liefert dann:

4.2
a)
Der Punkt  hat die gleichen
hat die gleichen  - und
- und  -Koordinaten wie
-Koordinaten wie  und die gleiche
und die gleiche  -Koordinate wie
-Koordinate wie  Somit folgen die Koordinaten von
Somit folgen die Koordinaten von  mit
mit 
b)
Die Raumdiagonalen des Quaders  schneiden sich genau in der Mitte des Quaders.
Eine Raumdiagonale des Quaders wird beispielsweise durch die Strecke
schneiden sich genau in der Mitte des Quaders.
Eine Raumdiagonale des Quaders wird beispielsweise durch die Strecke  dargestellt. Für den Mittelpunkt dieser Strecke gilt
dargestellt. Für den Mittelpunkt dieser Strecke gilt  und somit
und somit  Für
Für  gilt also:
gilt also:
 Die Koordinaten des Punkts
Die Koordinaten des Punkts  sind somit gegeben durch
sind somit gegeben durch 
c)
Ein Eckpunkt des neuen Quaders  der nur positive Koordinaten hat, ist
der nur positive Koordinaten hat, ist  Es gilt:
Es gilt:

4.3
a)
b)
Mit dem Einsatz von 3 Euro und der Auszahlung von 10 Euro für jedes Erzielen eines grünen Sektors ergibt sich der Erwartungswert für den Veranstalter zu:
Der erwartete Gewinn des Veranstalters pro Spiel beträgt somit 1 Euro.