Stochastik 3.2

Sportfan

Gemäß einer „Studie zur Gesundheit Erwachsener in Deutschland“ zeigt sich in Deutschland ein Trend zu mehr sportlicher Aktivität.

Ein Viertel der Erwachsenen treibt regelmäßig mindestens zwei Stunden Sport pro Woche (Sportfans), wobei der Anteil der Sportfans unter den Männern mit $29,3\%$ etwas höher ist als unter den Frauen.

Alle anderen Bundesbürger werden hier als „keine Sportfans" bezeichnet.

Berechne die Wahrscheinlichkeit der folgenden Ereignisse:

A :

Nur der zweite und sechste von zehn zufällig ausgewählten Bundesbürgern sindSportfans.

B :

Unter $20$ zufällig ausgewählten männlichen Bundesbürgern befinden sich genau drei Sportfans.

C :

Unter zehn zufällig ausgewählten Bundesbürgern befindet sich höchstens ein Sportfan.

D :

Von $100$ zufällig ausgewählten Bundesbürgern gehören mindestens $70$ und weniger als $79$ Personen zu denjenigen, die keine Sportfans sind.

E :

Unter $850$ zufällig ausgewählten männlichen Bundesbürgern befinden sich genau $609$ Personen, die keine Sportfans sind.

(12P)

Bestimme die Anzahl der Bundesbürger, die mindestens befragt werden müssten, um mit einer Wahrscheinlichkeit von mindestens $0,96$ wenigstens einen zu entdecken, der Sportfan ist.

(3P)

Unter allen Bundesbürgern liegt der Anteil der Männer bei $48,88\%$ (Zensus 2011).

Berechne die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Sportfan ein Mann ist.

Bestimme den Anteil der Sportfans unter den Frauen.

(8P)

In einem Sportstudio trainieren $25$ Bundesbürger, von denen genau acht zur Gruppe der Sportfans gehören. Es werden zufällig sieben Personen „ohne Zurücklegen“ ausgewählt.

Berechne die Wahrscheinlichkeit des Ereignisses $F$ , dass sich unter den sieben ausgewählten Personen genau drei Sportfans befinden.

(3P)

Eine Gruppe umfasst $n$ zufällig ausgewählte Bundesbürger. Untersuche, für welche Gruppengröße n die Wahrscheinlichkeit, genau einen Sportfan in der Gruppe zu haben, am größten ist.

(4P)

Aufgabe 3.2

$\blacktriangleright$ Wahrscheinlichkeiten berechnen

Der Aufgabenstellung entnimmst du, dass ein Viertel der Erwachsenen zu den „Sportfans“ gehört. Der Anteil der Sportfans unter den Männern beträgt $29,3\%$ . Du sollst verschiedene Ereignisse betrachten:

$\blacktriangleright$ A: Nur der zweite und der sechste von zehn zufällig ausgewählten Personen sind Sportfans.

Die Wahrscheinlichkeit, dass eine zufällig befragte Person ein Sportfan ist, beträgt $0,25$ . Es werden zehn Personen betrachtet. Nur die zweite und die sechste Person sollen Sportfans sein. Die Wahrscheinlichkeit setzt sich mit der Pfadmultiplikationsregel wie folgt zusammen:

$P(A)$ $= 0,75 \cdot 0,25 \cdot 0,75^3 \cdot 0,25 \cdot 0,75^4$ $= 0,0063$

Die gesuchte Wahrscheinlichkeit beträgt somit $0,63\%$ .

$\blacktriangleright$ B: Unter 20 zufällig ausgewählten männlichen Bundesbürgern befinden sich genau drei Sportfans.

In diesem Aufgabenteil hilft dir die Binomialverteilung. Um diese zu verwenden, benötigst du eine Zufallsvariable, welche die Anzahl von Treffern beschreibt. Ein Treffer ist hier eine Person, die zu den Sportfans zählt. Deine neue Zufallsvariable ist:

$X: \text{„Anzahl der Sportfans}$ $\text{unter den befragten Personen.“}$

Diese Zufallsvariable ist binomialverteilt.

Die Wahrscheinlichkeit für $3$ Treffer aus $20$ zufällig ausgewählten Bundesbürgern mit einer Wahrscheinlichkeit von $p=0,293$ berechnest du mit deinem CAS wie folgt:

menu $\rightarrow$ 5: Wahrscheinlichkeit $\rightarrow$ 5: Verteilungen $\rightarrow$ D: BinomialPdf

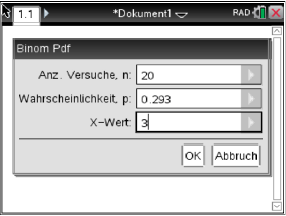Eingabemaske für die Binomialverteilung mit Feldern für Versuche, Wahrscheinlichkeit und X-Wert.

Abb. 1: Eingetragene Daten

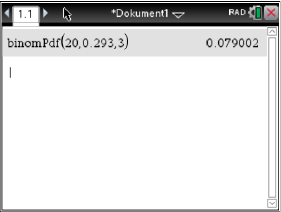Screenshot einer Softwareanwendung mit einem Berechnungsbeispiel für die Binomialverteilung.

Abb. 2: Ergebnis

Die gesuchte Wahrscheinlichkeit beträgt also $7,9 \%$ .

$\blacktriangleright$ C: Unter zehn zufällig ausgewählten Bundesbürgern befindet sich höchstens ein Sportfan.

Auch hier kannst du die Binomialverteilung nutzen. Da du jetzt zehn Personen, die nicht unbedingt männlich sein müssen, betrachtest, ändern sich die Parameter zu $p=0,25$ und $n=10$ . Damit kannst du die gesuchte Wahrscheinlichkeit $P(X\leq 1)$ berechnen.Die gesuchte Wahrscheinlichkeit kannst du nun mit deinem CAS folgendermaßen bestimmen:

menu $\rightarrow$ 5: Wahrscheinlichkeit $\rightarrow$ 5: Verteilungen $\rightarrow$ D: BinomialCdf

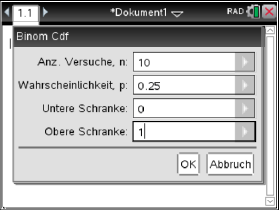Eingabemaske für Binomialverteilung mit Feldern für Versuche, Wahrscheinlichkeit und Schranken.

Abb. 3: Eingetragene Daten

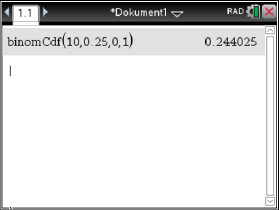Ein Bildschirm mit einer Berechnung zur binomialen kumulativen Verteilungsfunktion.

Abb. 4: Ergebnis

Die gesuchte Wahrscheinlichkeit beträgt also $24,4\%$ .

$\blacktriangleright$ D: Von $\boldsymbol{100}$ zufällig ausgewählten Personen gehören mindestens $\boldsymbol{70}$ und weniger als $\boldsymbol{79}$ Personen zu denjenigen, die keine Sportfans sind.

Auch in diesem Aufgabenteil kannst du die binomialverteilte Zufallsvariable $X$ verwenden. Da du wieder alle Erwachsenen betrachtest, verwendest du $n=100$ . Hier betrachtest du als Treffer, wenn eine Person kein Sportfan ist. Deswegen verwendest du $p=0,75$ .

Die gesuchte Wahrscheinlichkeit kannst du wie folgt berechnen:

$\begin{array}[t]{rll} P(D)&=&P(70 \le X \lt 79) &\quad \scriptsize \\[5pt] &=& P(X \leq 78)-P(X \le 69) \end{array}$

Diese Wahrscheinlichkeiten kannst du erneut mit deinem CAS berechnen:

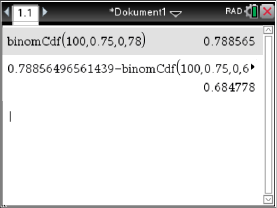Mathematische Berechnungen in einem digitalen Dokument, inklusive binomialer Funktionen.

Abb. 5: Ergebnis

Die gesuchte Wahrscheinlichkeit beträgt also $68,48\%$ .

$\blacktriangleright$ E: Unter $850$ zufällig ausgewählten männlichen Bundesbürgern befinden sich genau $609$ , die keine Sportfans sind.

Auch in diesem Aufgabenteil kannst du die binomialverteilte Zufallsvariable $X$ verwenden. Hierbei verwendest du $n=850$ . Hier betrachtest du als Treffer, wenn eine männliche Person kein Sportfan ist. Deswegen verwendest du $p=0,707$ .

Die gesuchte Wahrscheinlichkeit $P(X=609)$ kannst du wie folgt mit deinem CAS berechnen:

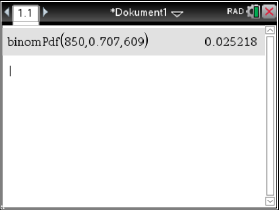Screenshot einer Berechnung mit der Funktion binomPdf auf einem Rechner.

Abb. 6: Ergebnis

Die gesuchte Wahrscheinlichkeit beträgt also $2,52\%$ .

$\blacktriangleright$ Anzahl der Bundesbürger bestimmen

In dieser Aufgabe betrachtest du wieder die binomialverzeilte Zufallsvariable $X$ , welche die Anzahl der Sportfans beschreibt. Der Unterschied ist, dass hier die Anzahl $n$ der befragten Personen gesucht ist und du dafür eine Information über die Anzahl der Treffer gegeben hast.

Du sollst also ein $n$ bestimmen, sodass die Gleichung

$\begin{array}[t]{rll} P(X \ge 1)&\ge&0,96 \end{array}$

erfüllt ist. Da die Wahrscheinlichkeit, dass aus $n$ ausgewählten Personen keiner Sportfan ist bei $0,75^n$ liegt, kannst du wie folgt umformen:

$\begin{array}[t]{rll} P(x \ge 1)&=& 1- 0,75 ^n \end{array}$

Vollständige Lösung anzeigen

Bei der Umformung verwendest du, dass $\binom{n}{0}=1$ ist.

Um jetzt $n$ zu bestimmen, musst du die folgende Ungleichung nach $n$ auflösen:

$\begin{array}[t]{rll} 11,189 & \le & n \end{array}$

Vollständige Lösung anzeigen

Achtung: Im letzten Umformungsschritt dreht sich das Ungleichheitszeichen um, da $\ln(0,75)$ negativ ist.

Es müssen also mindestens $12$ Bundesbürger befragt werden, um mit einer Wahrscheinlichkeit und mindestens $0,96$ wenigstens einen zu entdecken, der Sportfan ist.

$\blacktriangleright$ Wahrscheinlichkeit, dass ein Sportfan ein Mann ist, bestimmen

Bei der gesuchten Wahrscheinlichkeit handelt es sich um eine bedingte Wahrscheinlichkeit. Um diese besser beschreiben zu können, solltest du dir die folgenden Ereignisse definieren:

$M:$ „Die befragte Person ist männlich.“

$F:$ „Die befragte Person ist ein Sportfan.“

Für diese drei Ereignisse kannst du die Wahrscheinlichkeiten aus der Aufgabenstellung ablesen:

$P(M)=0,4888$ und $P(F)=0,25$ . Außerdem ist die Wahrscheinlichkeit $P(F \mid M)= 0,293$ angegeben.

Du kannst die gesuchte Wahrscheinlichkeit jetzt mit der Bayes- Formel berechnen:

$\begin{array}[t]{rll} P(M \mid F)&=&\dfrac{P(F \mid M)\cdot P(M)}{P(F)} \\ &=& \dfrac{0,293 \cdot 0,4888}{0,25}\\ &\approx& 0,573 \end{array}$

Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Sprotfan ein Mann ist, beträgt also $57,3 \%$ .

$\blacktriangleright$ Anteil der Sportfans unter den Frauen bestimmen

Um die Wahrscheinlichkeit beschreiben zu können, betrachtest du das Gegenereignis von E:

$\overline{M}:$ „Die befragte Person ist weiblich.“

Mit der Wahrscheinlichkeit: $P(\overline{M})=1-P(M)=0,5112$

Der Anteil der Sportfans unter den Frauen entspricht der bedingten Wahrscheinlichkeit $P(F \mid \overline{M})$ , die du mit der Formel der totalen Wahrscheinlichkeit bestimmen kannst:

$P(F)$ $=P(F \mid M)\cdot P(M)+P(F \mid \overline{M})\cdot P(\overline{M})$

Dafür musst du die Formel nach $P(F \mid \overline{M})$ auflösen:

$\begin{array}[t]{rll} P(F \mid \overline{M})&\approx& 0,209 \end{array}$

Vollständige Lösung anzeigen

Der Anteil der Sportfans unter den Frauen beträgt somit $20,9\%$ .

$\blacktriangleright$ Wahrscheinlichkeit für $\boldsymbol{E}$ berechnen

Da jeder Bundesbürger, der in dem Sportstudio trainiert, mit der gleichen Wahrscheinlichkeit ausgewählt wird, kannst du von einem Laplace-Modell ausgehen. Die Wahrscheinlichkeiten in einem Laplace-Modell berechnest du, indem du die Anzahl der Möglichkeiten, die für dein Ereignis günstig sind durch die Anzahl aller möglichen Ausgänge teilst.

Also

$P(E)$ $=\dfrac{\text{Anzahl der günstigen Ergebnisse}}{\text{Anzahl aller möglichen Ergebnisse}}$

Schritt 1:Anzahl aller möglichen Ausgänge bestimmen

In dieser Aufgabe entspricht die Anzahl aller möglichen Ausgänge der Anzahl der Möglichkeiten, aus den $25$ Bundesbürgern $8$ zu ziehen. Da die Reihenfolge, mit der die Personen „gezogen“ werden nicht relevant ist, berechnest du diese Anzahl mit dem Binomialkoeffizienten.

$\text{Anzahl aller möglichen Ergebnisse}=\binom{25}{7}$

Schritt 2:Anzahl aller günstigen Ergebnisse bestimmen

Um ein günstiges Ergebnis handelt es sich, wenn aus den $8$ Sportfans genau drei und aus den $17$ Personen, die keine Sportfans sind, genau 4 ausgewählt werden. Auch hier spielt die Reihenfolge keine Rolle, weswegen du den Binomialkoeffizienten verwendest.

Die Anzahl der günstigen Ergebnisse setzt sich also folgendermaßen zusammen:

$\text{Anzahl der günstigen Ergebnisse}$ $= \binom{8}{3}\cdot \binom{17}{4}$

Damit kannst du die gesuchte Wahrscheinlichkeit berechnen:

$P(E)=\dfrac{\binom{8}{3} \cdot \binom{17}{4}}{\binom{25}{7}} = 0,277$

Die Wahrscheinlichkeit dafür, dass sich unter sieben zufällig ausgewählten Personen genau drei Sportfans befinden, beträgt $27,7\%$ .

$\blacktriangleright$ Anzahl Gruppenmitglieder bestimmen

Betrachte die Zufallsgröße $X_n,$ die die zufällige Anzahl der Sportfans in der Gruppe von $n$ zufällig ausgewählten Bundesbürgern beschreibt. Diese kann als binomialverteilt mit unbekanntem $n$ und $p=0,25$ angenommen werden.

Die Wahrscheinlichkeit dafür, dass sich in dieser Gruppe genau ein Sportfan befindet kann daher mit der Formel für die Binomialverteilung wie folgt dargestellt werden:

$\begin{array}[t]{rll} P(X_n = 1)&=& \binom{n}{1}\cdot 0,25^1 \cdot 0,75^{n-1} \\[5pt] &=& n \cdot 0,25 \cdot 0,75^{n-1} \end{array}$

Diese Wahrscheinlichkeit soll maximal sein. Bestimme mithilfe des CAS also das $n,$ für das der Funktionswert der folgenden Funktion in Abhängigkeit von $n$ maximal wird:

$f(n) = n \cdot 0,25 \cdot 0,75^{n-1}$

Definiere dazu die erste und zweite Ableitungsfunktion von $f$ in deinem CAS. Den Befehl für die Ableitung findest du unter:

menu $\to$ 4: Analysis $\to$ 1: Ableitung

Wende anschließend das notwendige Kriterium für Extremstellen an, in dem du die Gleichung $f‘(n)=0$ mit dem solve-Befehl löst. Du erhältst mögliche Extremstellen von $f:$

$\begin{array}[t]{rll} f‘(n) &=& 0 \\[5pt] n_1 &\approx& 3,48 \\[5pt] n_2 &\approx& 1733,01 \end{array}$

Überprüfe nun das hinreichende Kriterium für Extremstellen mithilfe der zweiten Ableitung:

$\begin{array}[t]{rll} f‘‘(n_1)&\approx& -0,035 \\[5pt] f‘‘(n_2)&\approx& 1,4\cdot 10^{-215} \end{array}$

An der Stelle $n_1$ besitzt $f$ also ein Maximum. Da die Anzahl der Gruppenmitglieder aber nur eine ganze Zahl sein kann, musst du noch überprüfen, ob die Wahrscheinlichkeit für $n=3$ oder $n=4$ am größten ist:

$\begin{array}[t]{rll} f(3)&=& \frac{27}{64} \\[5pt] f(4) &=& \frac{27}{64} \end{array}$

Die Wahrscheinlichkeit, dass sich genau ein Sportfan in der Gruppe befindet ist also am höchsten, wenn die Gruppe aus 3 oder 4 Mitgliedern besteht.

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

[6]

Aufgabe 3.2

$\blacktriangleright$ Wahrscheinlichkeiten berechnen

$\blacktriangleright$ A: Nur der zweite und der sechste von zehn zufällig ausgewählten Personen sind Sportfans.

$P(A)$ $= 0,75 \cdot 0,25 \cdot 0,75^3 \cdot 0,25 \cdot 0,75^4$ $= 0,0063$

Die gesuchte Wahrscheinlichkeit beträgt somit $0,63\%$ .

$\blacktriangleright$ B: Unter 20 zufällig ausgewählten männlichen Bundesbürgern befinden sich genau drei Sportfans.

$X: \text{„Anzahl der Sportfans}$ $\text{unter den befragten Personen.“}$

Diese Zufallsvariable ist binomialverteilt.

Die Wahrscheinlichkeit für $3$ Treffer aus $20$ zufällig ausgewählten Bundesbürgern mit einer Wahrscheinlichkeit von $p=0,293$ berechnest du mit deinem CAS wie folgt:

Interaktiv $\rightarrow$ Verteilungsfunktionen $\rightarrow$ Diskret $\rightarrow$ binomialPDf

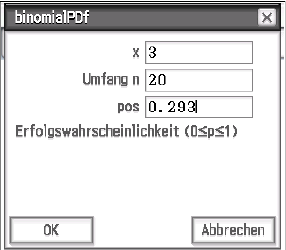Fenster eines Programms zur Berechnung der binomialen Wahrscheinlichkeitsfunktion mit Eingabefeldern.

Abb. 1: Eingetragene Daten

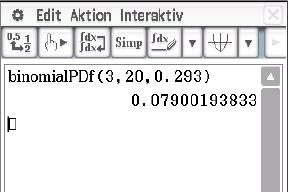Bildschirmansicht eines mathematischen Programms mit einer Berechnung zur Binomialverteilung.

Abb. 2: Ergebnis

Die gesuchte Wahrscheinlichkeit beträgt also $7,9 \%$ .

$\blacktriangleright$ C: Unter zehn zufällig ausgewählten Bundesbürgern befindet sich höchstens ein Sportfan.

Interaktiv $\rightarrow$ Verteilungsfunktionen $\rightarrow$ Diskret $\rightarrow$ binomialCDf

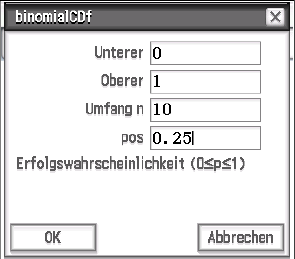Dialogfenster zur Berechnung der binomialen kumulativen Verteilungsfunktion mit Eingabefeldern.

Abb. 3: Eingetragene Daten

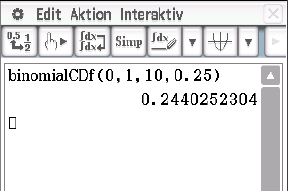Screenshot einer mathematischen Software mit einer Berechnung der binomialen kumulativen Verteilungsfunktion.

Abb. 4: Ergebnis

Die gesuchte Wahrscheinlichkeit beträgt also $24,4\%$ .

Die gesuchte Wahrscheinlichkeit kannst du wie folgt berechnen:

$\begin{array}[t]{rll} P(D)&=&P(70 \le X \lt 79) &\quad \scriptsize \\[5pt] &=& P(X \leq 78)-P(X \le 69) \end{array}$

Diese Wahrscheinlichkeiten kannst du erneut mit deinem CAS berechnen:

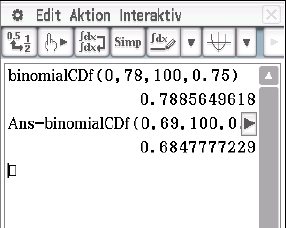Screenshot einer Software mit Berechnungen zur binomialen kumulativen Verteilungsfunktion.

Abb. 5: Ergebnis

Die gesuchte Wahrscheinlichkeit beträgt also $68,48\%$ .

$\blacktriangleright$ E: Unter $850$ zufällig ausgewählten männlichen Bundesbürgern befinden sich genau $609$ , die keine Sportfans sind.

Die gesuchte Wahrscheinlichkeit $P(X=609)$ kannst du wie folgt mit deinem CAS berechnen:

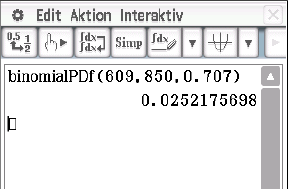Mathematische Software zeigt die Berechnung einer Binomialverteilung an.

Abb. 6: Ergebnis

Die gesuchte Wahrscheinlichkeit beträgt also $2,52\%$ .

$\blacktriangleright$ Anzahl der Bundesbürger bestimmen

Du sollst also ein $n$ bestimmen, sodass die Gleichung

$\begin{array}[t]{rll} P(X \ge 1)&\ge&0,96 \end{array}$

erfüllt ist. Da die Wahrscheinlichkeit, dass aus $n$ ausgewählten Personen keiner Sportfan ist bei $0,75^n$ liegt, kannst du wie folgt umformen:

$\begin{array}[t]{rll} P(x \ge 1)&=& 1- 0,75 ^n \end{array}$

Vollständige Lösung anzeigen

Bei der Umformung verwendest du, dass $\binom{n}{0}=1$ ist.

Um jetzt $n$ zu bestimmen, musst du die folgende Ungleichung nach $n$ auflösen:

$\begin{array}[t]{rll} 11,189 & \le & n \end{array}$

Vollständige Lösung anzeigen

Achtung: Im letzten Umformungsschritt dreht sich das Ungleichheitszeichen um, da $\ln(0,75)$ negativ ist.

Es müssen also mindestens $12$ Bundesbürger befragt werden, um mit einer Wahrscheinlichkeit und mindestens $0,96$ wenigstens einen zu entdecken, der Sportfan ist.

$\blacktriangleright$ Wahrscheinlichkeit, dass ein Sportfan ein Mann ist, bestimmen

Bei der gesuchten Wahrscheinlichkeit handelt es sich um eine bedingte Wahrscheinlichkeit. Um diese besser beschreiben zu können, solltest du dir die folgenden Ereignisse definieren:

$M:$ „Die befragte Person ist männlich.“

$F:$ „Die befragte Person ist ein Sportfan.“

Für diese drei Ereignisse kannst du die Wahrscheinlichkeiten aus der Aufgabenstellung ablesen:

$P(M)=0,4888$ und $P(F)=0,25$ . Außerdem ist die Wahrscheinlichkeit $P(F \mid M)= 0,293$ angegeben.

Du kannst die gesuchte Wahrscheinlichkeit jetzt mit der Bayes- Formel berechnen:

$\begin{array}[t]{rll} P(M \mid F)&=&\dfrac{P(F \mid M)\cdot P(M)}{P(F)} \\ &=& \dfrac{0,293 \cdot 0,4888}{0,25}\\ &\approx& 0,573 \end{array}$

Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Sprotfan ein Mann ist, beträgt also $57,3 \%$ .

$\blacktriangleright$ Anteil der Sportfans unter den Frauen bestimmen

Um die Wahrscheinlichkeit beschreiben zu können, betrachtest du das Gegenereignis von E:

$\overline{M}:$ „Die befragte Person ist weiblich.“

Mit der Wahrscheinlichkeit: $P(\overline{M})=1-P(M)=0,5112$

Der Anteil der Sportfans unter den Frauen entspricht der bedingten Wahrscheinlichkeit $P(F \mid \overline{M})$ , die du mit der Formel der totalen Wahrscheinlichkeit bestimmen kannst:

$P(F)$ $=P(F \mid M)\cdot P(M)+P(F \mid \overline{M})\cdot P(\overline{M})$

Dafür musst du die Formel nach $P(F \mid \overline{M})$ auflösen:

$\begin{array}[t]{rll} P(F \mid \overline{M})&\approx& 0,209 \end{array}$

Vollständige Lösung anzeigen

Der Anteil der Sportfans unter den Frauen beträgt somit $20,9\%$ .

$\blacktriangleright$ Wahrscheinlichkeit für $\boldsymbol{E}$ berechnen

Da jeder Bundesbürger, der in dem Sportstudio trainiert, mit der gleichen Wahrscheinlichkeit ausgewählt wird, kannst du von einem Laplace Modell ausgehen. Die Wahrscheinlichkeiten in einem Laplace Modell berechnest du, indem du die Anzahl der Möglichkeiten, die für dein Ereignis günstig sind durch die Anzahl aller möglichen Ausgänge teilst.

Also

$P(E)$ $=\dfrac{\text{Anzahl der günstigen Ergebnisse}}{\text{Anzahl aller möglichen Ergebnisse}}$

Schritt 1:Anzahl aller möglichen Ausgänge bestimmen

$\text{Anzahl aller möglichen Ergebnisse}=\binom{25}{7}$

Schritt 2:Anzahl aller günstigen Ergebnisse bestimmen

Die Anzahl der günstigen Ergebnisse setzt sich also folgendermaßen zusammen:

$\text{Anzahl der günstigen Ergebnisse}$ $= \binom{8}{3}\cdot \binom{17}{4}$

Damit kannst du die gesuchte Wahrscheinlichkeit berechnen:

$P(E)=\dfrac{\binom{8}{3} \cdot \binom{17}{4}}{\binom{25}{7}} = 0,277$

Die Wahrscheinlichkeit dafür, dass sich unter sieben zufällig ausgewählten Personen genau drei Sportfans befinden, beträgt $27,7\%$ .

$\blacktriangleright$ Anzahl Gruppenmitglieder bestimmen

Die Wahrscheinlichkeit dafür, dass sich in dieser Gruppe genau ein Sportfan befindet kann daher mit der Formel für die Binomialverteilung wie folgt dargestellt werden:

$\begin{array}[t]{rll} P(X_n = 1)&=& \binom{n}{1}\cdot 0,25^1 \cdot 0,75^{n-1} \\[5pt] &=& n \cdot 0,25 \cdot 0,75^{n-1} \end{array}$

Diese Wahrscheinlichkeit soll maximal sein. Bestimme mithilfe des CAS also das $n,$ für das der Funktionswert der folgenden Funktion in Abhängigkeit von $n$ maximal wird:

$f(n) = n \cdot 0,25 \cdot 0,75^{n-1}$

Definiere dazu die erste und zweite Ableitungsfunktion von $f$ in deinem CAS. Den Befehl für die Ableitung findest du unter:

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

Wende anschließend das notwendige Kriterium für Extremstellen an, in dem du die Gleichung $f‘(n)=0$ mit dem solve-Befehl löst. Du erhältst mögliche Extremstellen von $f:$

$\begin{array}[t]{rll} f‘(n) &=& 0 \\[5pt] n_1 &\approx& 3,48 \\[5pt] n_2 &\approx& 1733,01 \end{array}$

Überprüfe nun das hinreichende Kriterium für Extremstellen mithilfe der zweiten Ableitung:

$\begin{array}[t]{rll} f‘‘(n_1)&\approx& -0,035 \\[5pt] f‘‘(n_2)&\approx& 1,4\cdot 10^{-215} \end{array}$

$\begin{array}[t]{rll} f(3)&=& \frac{27}{64} \\[5pt] f(4) &=& \frac{27}{64} \end{array}$

Die Wahrscheinlichkeit, dass sich genau ein Sportfan in der Gruppe befindet ist also am höchsten, wenn die Gruppe aus 3 oder 4 Mitgliedern besteht.

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

[6]