Pflichtaufgaben

1.1 Analysis

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ mit $f_a(x)=a x^3+a x^2$ und $a \in \mathbb{R}^+.$

Gib den Wert von $a$ an, so dass der Punkt $(1 \mid 6)$ auf dem Graphen von $f_a$ liegt.

(1 BE)

Berechne in Abhängigkeit von $a$ den Inhalt der Fläche, die der Graph von $f_a$ mit der $x$ -Achse einschließt.

(4 BE)

1.2 Analysis

Betrachtet wird die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ mit $f_a(x)=x \cdot \mathrm e^{a \cdot x}$ und $a \in \mathbb{R}, a \neq 0$ . Für jeden Wert von $a$ besitzt die Funktion $f_a$ genau eine Extremstelle.

Begründe, dass der Graph von $f_a$ für $x\lt0$ unterhalb der $x$ -Achse verläuft.

(2 BE)

Beide Abbildungen zeigen einen Graphen der Schar, eine der beiden für einen positiven Wert von $a.$ Entscheide, welche Abbildung dies ist, und begründe deine Entscheidung.

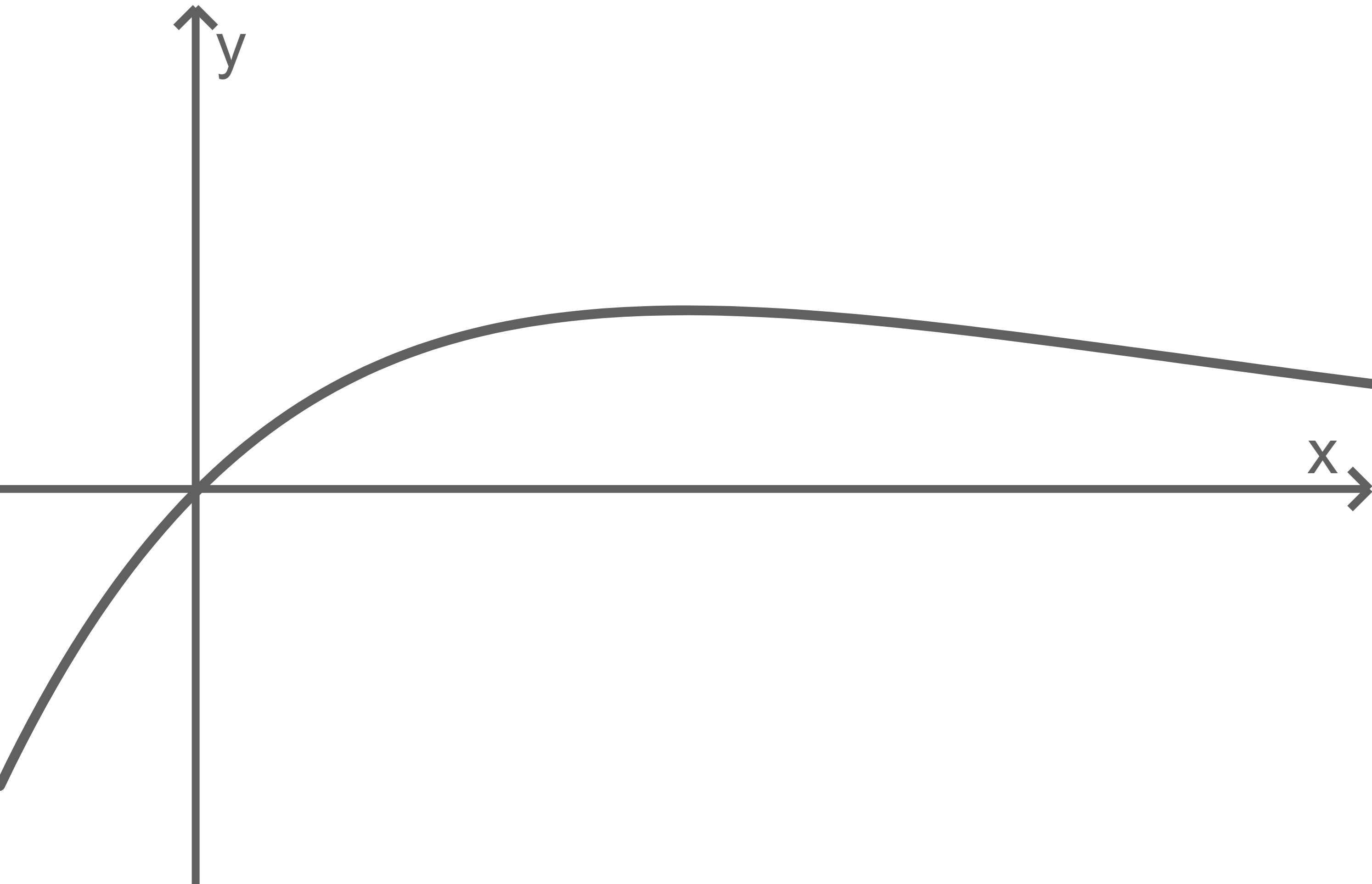
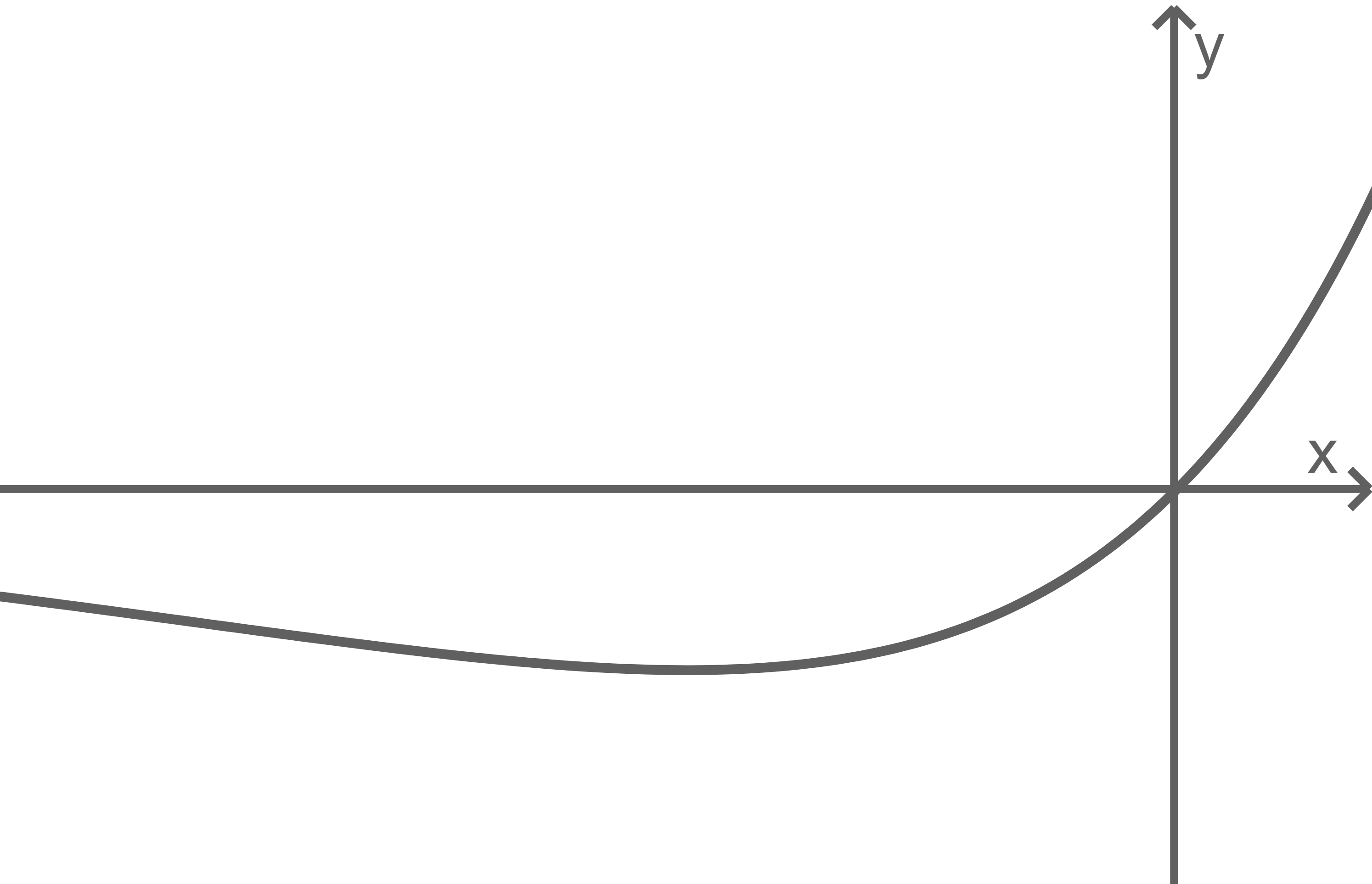
Abb. 1

Abb. 2

(3 BE)

1.3 Analytische Geometrie

Gegeben ist die Schar der Ebenen $E_a: 2 a x_1-4 x_2+(a-2) \cdot x_3=12$ mit $a \in \mathbb{R}.$

Ermittle denjenigen Wert von $a,$ für den $E_a$ parallel zur Gerade mit der Gleichung $\overrightarrow{x}=\pmatrix{0\\1\\1}+b \cdot\pmatrix{-1\\0\\1}$ und $b \in \mathbb{R}$ verläuft.

(2 BE)

Prüfe, ob die Ebene mit der Gleichung $6 x_1-8 x_2+x_3=24$ zur Schar gehört.

(3 BE)

1.4 Stochastik

In einer Urne befinden sich 3 grüne und 3 rote Kugeln, die sonst nicht unterscheidbar sind. Bei einer Ziehung werden nacheinander vier Kugeln ohne Zurücklegen gezogen.

Berechne die Wahrscheinlichkeit dafür, dass genau drei Kugeln mit gleicher Farbe aufeinander folgen.

(2 BE)

Die Anzahl der Kugeln wird so geändert, dass $n$ grüne und $n$ rote Kugeln in der Urne enthalten sind. Es werden nacheinander vier Kugeln ohne Zurücklegen gezogen. Begründe, dass die folgende Aussage richtig ist:

$\,$

Es gibt einen Wert für $n,$ so dass es weniger als 16 Möglichkeiten für die Reihenfolge der Farben gibt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1 Analysis

$\begin{array}[t]{rll} f_a(1)&=&6 \\[5pt] a\cdot1^3+a\cdot1^2&=&6 \\[5pt] 2a&=&6 &\quad \scriptsize \mid\;:2\\[5pt] a&=&3 \end{array}$

Nullstellen bestimmen

$\begin{array}[t]{rll} f_a(x)&=&0 \\[5pt] ax^3+ax^2&=&0 \\[5pt] ax^2\cdot(x+1)&=&0 \end{array}$

Da $ax^2=0$ wegen $a\in\mathbb{R}^+$ nur für $x=0$ gilt, folgt mit dem Satz des Nullprodukts $x_1=0$ und weiter:

$\begin{array}[t]{rll} x_2+1&=&0 &\quad \scriptsize \mid\;-1\\[5pt] x_2&=&-1 \end{array}$

Flächeninhalt berechnen

Rechenweg anzeigen

$A_a = \dfrac{1}{12}a$

1.2 Analysis

Da stets $\mathrm e^{a\cdot x}\gt 0$ gilt, folgt für $x\lt0$ immer $f_a(x)\lt0.$ Somit verläuft der Graph von $f_a$ in diesem Fall unterhalb der $x$ -Achse.

Für $a\gt0$ gilt:

Rechenweg anzeigen

$\lim\limits_{x\to+\infty}f_a(x) = +\infty$

Da die Funktion $f_a$ laut Aufgabenstellung für alle Werte von $a$ genau eine Extremstelle besitzt, fällt der Graph in Abbildung 1 für steigende Werte von $x$ weiter. Somit zeigt Abbildung 2 den Graphen der Schar mit positivem Wert von $a.$

1.3 Analytische Geometrie

Ein Normalenvektor $\overrightarrow{n}$ der Ebene $E_a$ lässt sich aus der Ebenengleichung wie folgt ablesen:

$\overrightarrow{n_a}=\pmatrix{2a\\-4\\a-2}$

Für den gesuchten Wert von $a$ folgt somit:

$\begin{array}[t]{rll} \pmatrix{2a\\-4\\a-2}\circ\pmatrix{-1\\0\\1}&=&0 \\[5pt] -2a+a-2&=&0 &\quad \scriptsize \mid\;+a\\[5pt] -2&=&a \end{array}$

Ein Normalenvektor der betrachteten Ebene lässt sich wie folgt ablesen:

$\overrightarrow{n}=\pmatrix{6\\-8\\1}$

Damit die Ebene zur Ebenenschar gehört, muss ein $k\in\mathbb{R}$ existieren, sodass gilt:

$\pmatrix{2a\\-4\\a-2}=k\cdot\pmatrix{6\\-8\\1}$

Aus der zweiten Zeile folgt $k=0,5.$ Somit ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&2a&=& 3 \\ \text{II}\quad&a-2&=&0,5 \end{array}$

Gleichung $\text{II}$ liefert $a=2,5.$ Da $2\cdot 2,5=5$ ergibt, liefert einsetzen von $a=2,5$ in Gleichung $\text{I}$ einen Widerspruch. Somit besitzt das Gleichungssystem keine Lösung und die betrachtete Ebene gehört damit nicht zur Schar.

1.4 Stochastik

Für das betrachtete Ereignis gibt es die folgenden vier Möglichkeiten, wobei $r$ für eine rote Kugel und $g$ für eine grüne Kugel steht:

$\big\{(r,r,r,g),(r,g,g,g),(g,g,g,r),$ $(g,r,r,r)\big\}$

Die Wahrscheinlichkeit, in den ersten drei Zügen drei Kugeln der gleichen Farbe zu ziehen, ergibt sich als $\frac{3}{6}\cdot\frac{2}{5}\cdot\frac{1}{4}\cdot\frac{3}{3}=\frac{1}{20}.$ Für die Wahrscheinlichkeit, die drei gleichfarbigen Kugeln in den letzten drei Züge zu ziehen, gilt $\frac{3}{6}\cdot\frac{3}{5}\cdot\frac{2}{4}\cdot\frac{1}{3}=\frac{1}{20}.$

Alle betrachteten Möglichkeiten besitzen somit die selbe Wahrscheinlichkeit, für die gesuchte Wahrscheinlichkeit $p$ folgt daher:

$p=4\cdot\dfrac{1}{20}=\dfrac{1}{5}$

Für z.B. $n=2$ existieren insgesamt nur sechs und damit weniger als 16 Möglichkeiten für die Reihenfolge der Farben, und zwar die folgenden:

$\big\{(r,r,g,g),(g,g,r,r),(r,g,g,r),$ $(g,r,r,g),(r,g,r,g),(g,r,g,r)\big\}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?