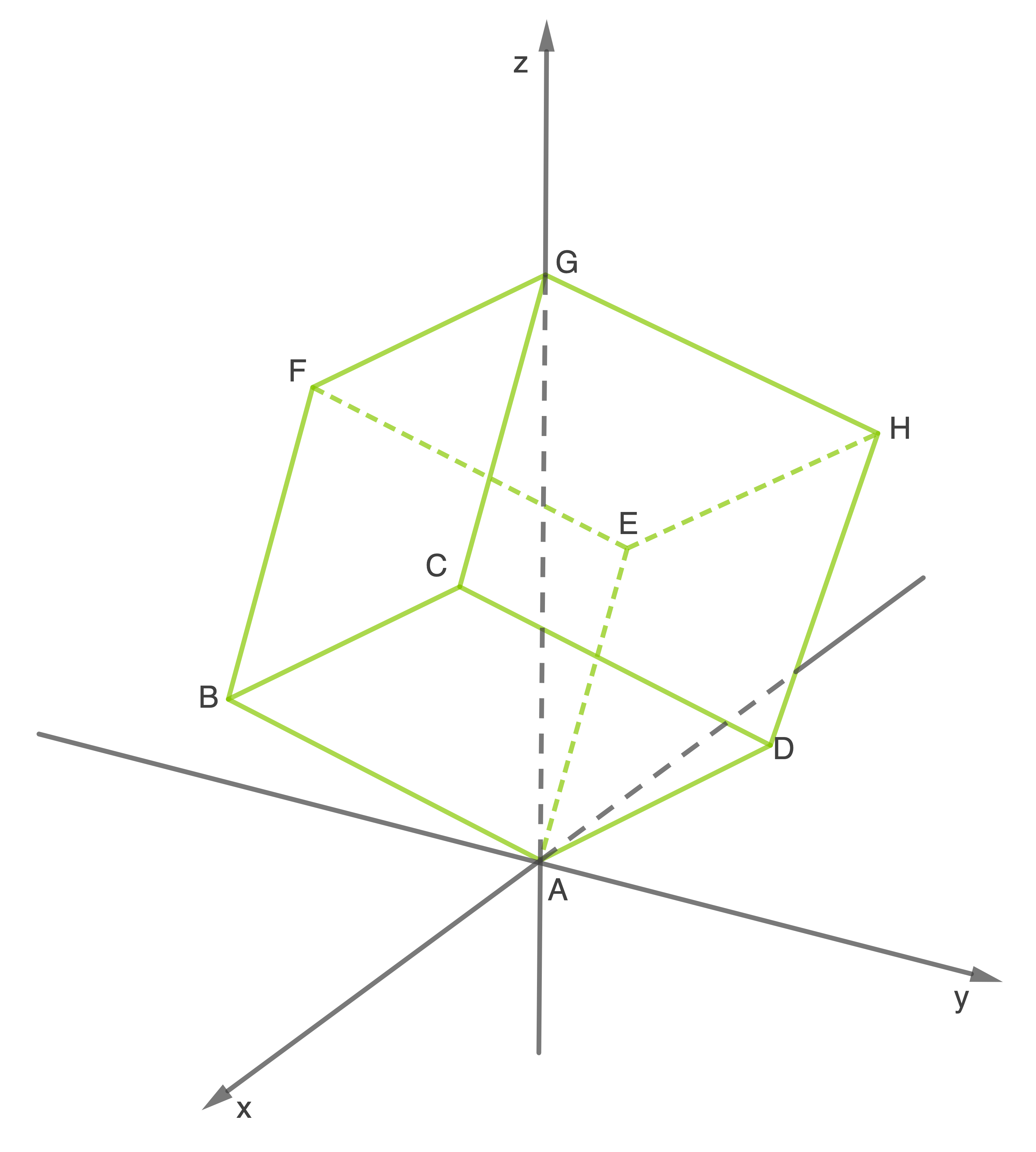
Analytische Geometrie 3.2 - Würfel
Betrachtet wird der abgebildete Würfel mit 

 und
und 
a)
Berechne das Volumen des Würfels.
(2 BE)
b)
Begründe, dass das Viereck  ein Rechteck ist, und zeichne dieses in die Abbildung ein.
ein Rechteck ist, und zeichne dieses in die Abbildung ein.
(3 BE)
c)
Das Viereck  liegt in der Ebene
liegt in der Ebene 
Bestimme eine Gleichung von in Parameterform und Koordinatenform.
[Kontrollergebnis:
in Parameterform und Koordinatenform.
[Kontrollergebnis:  ]
]
Bestimme eine Gleichung von
(5 BE)
d)
Bestimme die Größe des Winkels, den die Ebene  mit der
mit der  -Ebene einschließt.
-Ebene einschließt.
(2 BE)
e)
Ermittle die Koordinaten von  .
.
(5 BE)
f)
Die Ebene, die durch die Mittelpunkte der Kanten  und
und  verläuft, teilt den Würfel in zwei Teilkörper.
verläuft, teilt den Würfel in zwei Teilkörper.
Bergründe mithilfe einer Skizze, dass das Volumen des kleineren Teilkörpers ein Achtel des Volumens des Würfels ist.
Bergründe mithilfe einer Skizze, dass das Volumen des kleineren Teilkörpers ein Achtel des Volumens des Würfels ist.
(5 BE)
g)
Gegeben ist die Schar der Ebenen  mit
mit 
Gib in Abhängigkeit von die unterschiedlichen Arten der Figuren an, in denen die Ebenen für
die unterschiedlichen Arten der Figuren an, in denen die Ebenen für  den Würfel schneiden.
den Würfel schneiden.
Gib in Abhängigkeit von
(3 BE)
(25 BE)
a)
Volumen des Würfels berechnen:
Die Kantenlängen eines Würfels sind alle gleich lang und somit lässt sich das Volumen eines Würfels mit berechnen.
Kantenlänge
berechnen.
Kantenlänge  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\bigg\vert\,\overrightarrow{AB}\,\bigg\vert&=& \bigg\vert\,\pmatrix{3\\-3\\3}-\pmatrix{0\\0\\0}\,\bigg\vert \\[5pt]
&=& \sqrt{3^2+(-3)^2+3^2}\\[5pt]
&=& \sqrt{27}
\end{array}\)](https://mathjax.schullv.de/94cdfb2e7a7bd9f97d52fe2ae9719713921e0cbe1821028d731596f7c4c9ffa3?color=5a5a5a) Volumenberechnung:
Volumenberechnung:
![\(\begin{array}[t]{rll}
V_{\text{Würfel}}&=& \left(\sqrt{27}\right)^3 \\[5pt]
&=& 81\sqrt{3}\,[VE]\\[5pt]
&\approx& 140,30\,[VE]
\end{array}\)](https://mathjax.schullv.de/340470d31d1896a52cd29bd98d429e7f477cac36b8616d9e7b39765e354877cf?color=5a5a5a) Das Volumen des Würfels beträgt
Das Volumen des Würfels beträgt ![\(81\sqrt{3}\, [VE]\)](https://mathjax.schullv.de/6717084191c2d972697b9e24d7acf1bc595d1cc1a9b481bdb8fb8f2a3ecb2dfc?color=5a5a5a) .
.
Die Kantenlängen eines Würfels sind alle gleich lang und somit lässt sich das Volumen eines Würfels mit
b)
Form des Vierecks  begründen:
begründen:
Die Merkmale eines Rechtecks sind einerseits, dass alle Innenwinkel rechte Winkel sind, und dass die gegenüberliegenden Seiten gleich lang sind.
Die Kanten und
und  und die Seitendiagonalen
und die Seitendiagonalen  und
und  sind jeweils gleich lang.
sind jeweils gleich lang.
Da auf der Seitenfläche
auf der Seitenfläche  liegt, steht
liegt, steht  senkrecht zu
senkrecht zu  . Ebenso mit der selben Argumentation steht
. Ebenso mit der selben Argumentation steht  senkrecht zu
senkrecht zu  .
.
Mit diesen Seitenverhältnissen innerhalb des Würfels ist bewiesen, dass es sich bei um ein Rechteck handelt.
um ein Rechteck handelt.
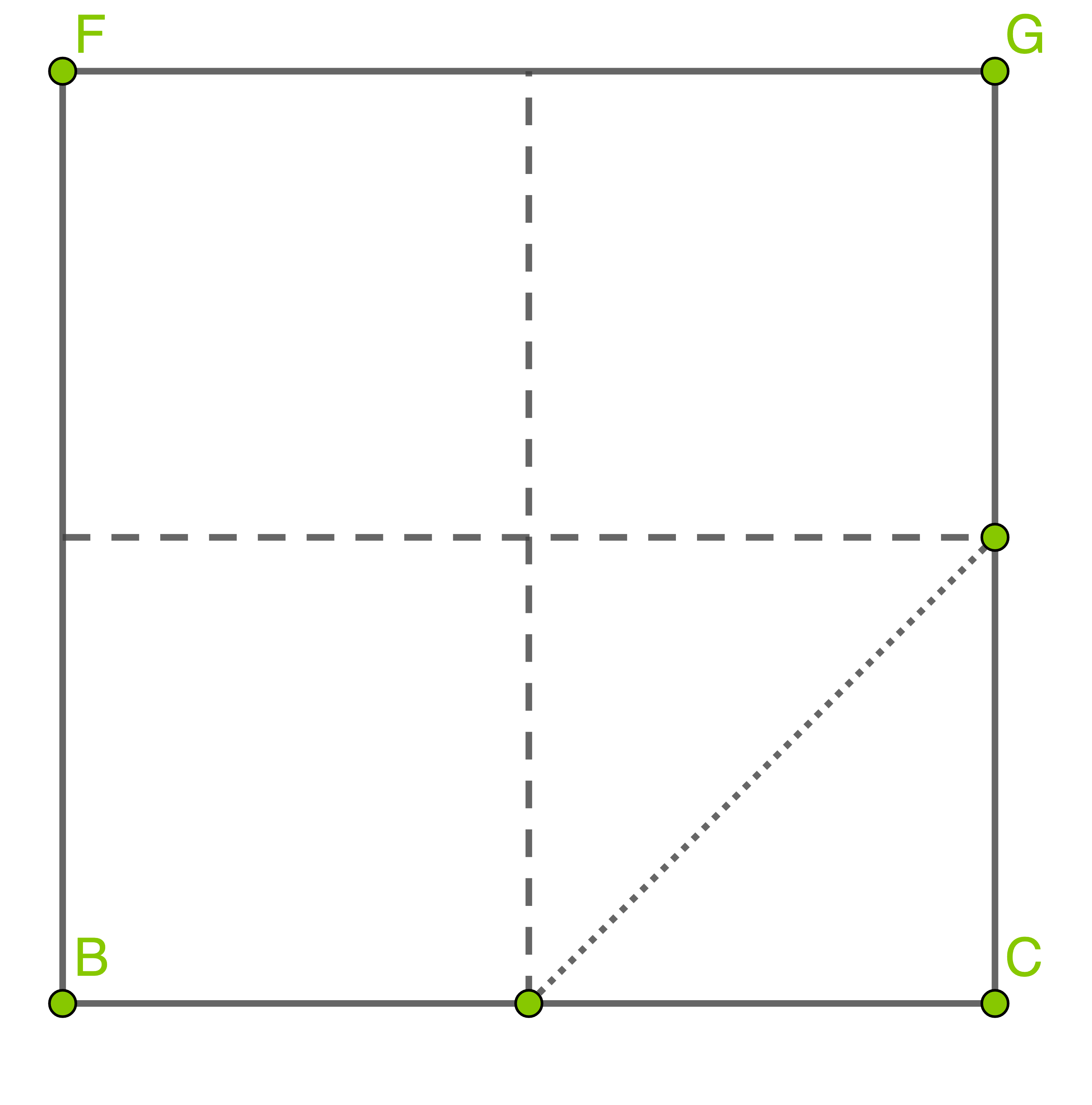
Rechteck zeichnen:
zeichnen:
Die Merkmale eines Rechtecks sind einerseits, dass alle Innenwinkel rechte Winkel sind, und dass die gegenüberliegenden Seiten gleich lang sind.
Die Kanten
Da
Mit diesen Seitenverhältnissen innerhalb des Würfels ist bewiesen, dass es sich bei
Rechteck
c)
Ebenengleichung  in Koordinatenform aufstellen:
in Koordinatenform aufstellen:
Spannvektoren und
und  aufstellen:
aufstellen:
![\(\begin{array}[t]{rll}
\overrightarrow{AB}&=& \pmatrix{3-0\\-3-0\\3-0}\\[5pt]
&=& \pmatrix{3\\-3\\3}
\end{array}\)](https://mathjax.schullv.de/1d79e750bc1931fecd7df6a0ffefebb1457f92e9875719cdbd4912b34c9b5525?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{AG}&=& \pmatrix{0-0\\0-0\\9-0}\\[5pt]
&=& \pmatrix{0\\0\\9}
\end{array}\)](https://mathjax.schullv.de/70317eb075878061a1029bfc2632677d5d09a393fac934e83970821555d55821?color=5a5a5a)
Normalenvektor aufstellen: Ein Normalenvektor kannst du mit dem Kreuzprodukt von
kannst du mit dem Kreuzprodukt von  und
und  berechnen.
Normalenform aufstellen und in Koordinatenform umwandeln:
berechnen.
Normalenform aufstellen und in Koordinatenform umwandeln:
![\(\begin{array}[t]{rll}
L:0&=& \pmatrix{1\\1\\0}\circ \left[\pmatrix{x\\y\\z}-\pmatrix{0\\0\\0}\right] \\[5pt]
L:0&=&x+y\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b33723c7e5b94fbccccd8906d6910bf9a8bd4f7baa3fae649beff9fc550338aa?color=5a5a5a) Eine Gleichung von
Eine Gleichung von  in Koordinatenform ist gegeben durch
in Koordinatenform ist gegeben durch  .
.
Spannvektoren
Normalenvektor aufstellen: Ein Normalenvektor
d)
Größe des Winkels  bestimmen:
bestimmen:
Ein Normalenvektor der -Ebene ist gegeben durch
-Ebene ist gegeben durch  .
.
Der Winkel, den die Ebene mit der
mit der  -Ebene einschließt, beträgt
-Ebene einschließt, beträgt  .
alternative Lösung:
Da
.
alternative Lösung:
Da  die
die  -Achse enthält und den Winkel halbiert, den die positive
-Achse enthält und den Winkel halbiert, den die positive  -Achse und die negative
-Achse und die negative  -Achse einschließen, beträgt die Größe des gesuchten Winkels
-Achse einschließen, beträgt die Größe des gesuchten Winkels  .
.
Ein Normalenvektor der
Der Winkel, den die Ebene
e)
Koordinaten des Punktes  bestimmen:
bestimmen:
Die Koordinaten des Mittelpunktes von
von  sind gegeben durch
sind gegeben durch  .
Koordinaten des Punktes
.
Koordinaten des Punktes  ermitteln:
Die Strecke
ermitteln:
Die Strecke  steht senkrecht zu der Ebene
steht senkrecht zu der Ebene  .
Die Koordinaten des Punktes
.
Die Koordinaten des Punktes  liegen bei
liegen bei  .
.
Die Koordinaten des Mittelpunktes
f)
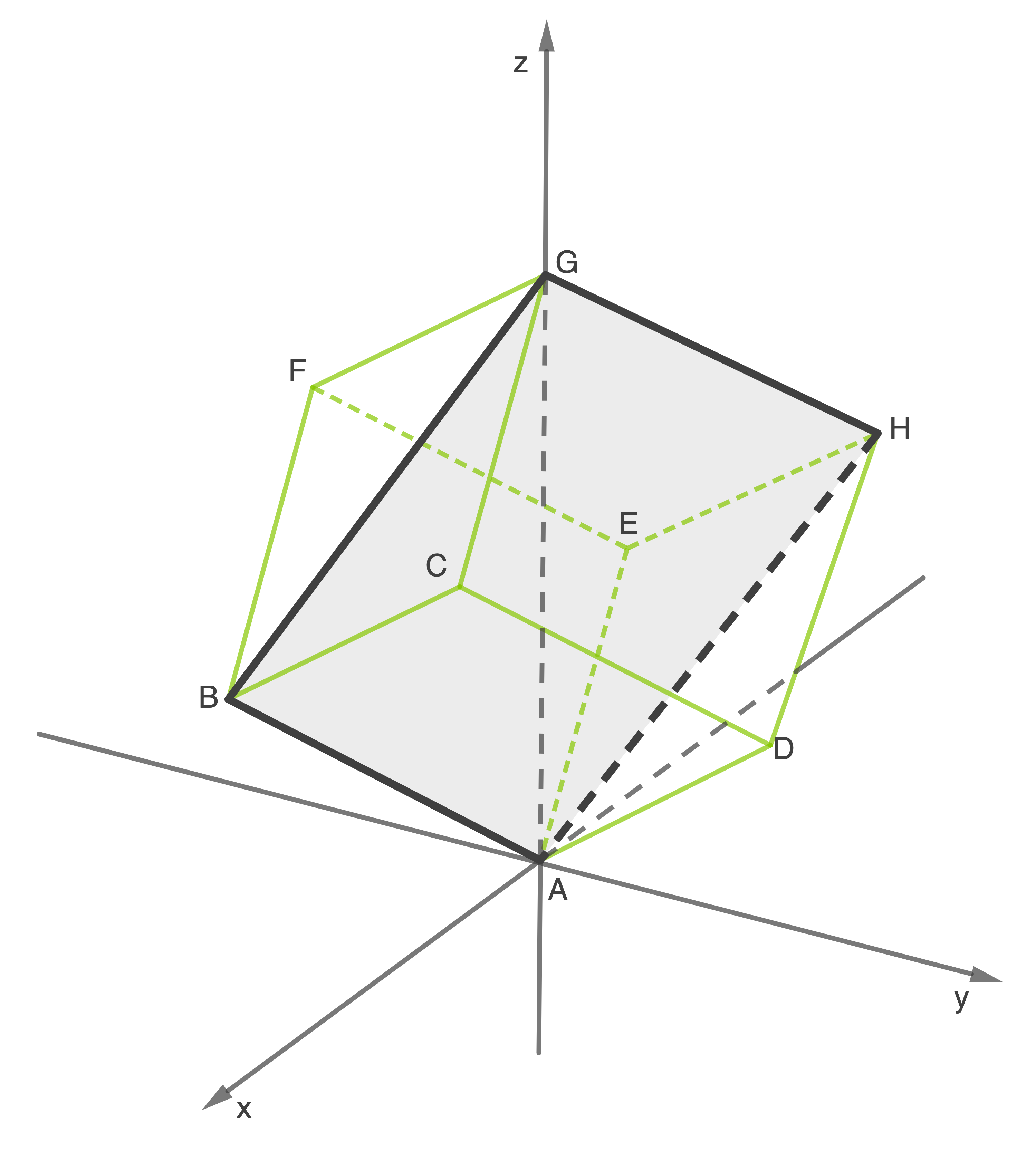
Volumen des kleineren Teilkörpers erläutern:
Skizze:
Begründung: Bei dem kleineren Teilkörper handelt es sich um ein Prisma, wessen Grundfläche eine Teilfläche der Seitenfläche ist. Der Inhalt dieser Teilfläche beträgt ein Achtel des Inhalts der Seitenfläche
ist. Der Inhalt dieser Teilfläche beträgt ein Achtel des Inhalts der Seitenfläche  . Die Höhe des Prismas stimmt mit der Kantenlänge des Würfels überein.
Damit ist bewiesen, dass das Volumen des kleineren Teilkörpers ein Achtel des Volumens des Würfels ist.
. Die Höhe des Prismas stimmt mit der Kantenlänge des Würfels überein.
Damit ist bewiesen, dass das Volumen des kleineren Teilkörpers ein Achtel des Volumens des Würfels ist.
Skizze:
Begründung: Bei dem kleineren Teilkörper handelt es sich um ein Prisma, wessen Grundfläche eine Teilfläche der Seitenfläche
g)
Schnittfiguren erläutern:
Für und
und  handelt es sich bei der jeweiligen Schnittfigur um ein Dreieck.
handelt es sich bei der jeweiligen Schnittfigur um ein Dreieck.
Für handelt es sich bei der jeweiligen Schnittfigur um ein Sechseck.
(Tipp: Um diese Vorangehensweise zu veranschaulichen, setze die Zahlen von
handelt es sich bei der jeweiligen Schnittfigur um ein Sechseck.
(Tipp: Um diese Vorangehensweise zu veranschaulichen, setze die Zahlen von  in die gegebene Schar ein und vergleiche die unterschiedlichen Figuren miteinander. Es kann auch helfen sich das Ganze einmal aufzuzeichnen.)
in die gegebene Schar ein und vergleiche die unterschiedlichen Figuren miteinander. Es kann auch helfen sich das Ganze einmal aufzuzeichnen.)
Für
Für