Analysis 2.1 - Trainingsstrecke
Durch die Gleichung  ist eine Funktionenschar
ist eine Funktionenschar  gegeben. Die Graphen dieser Schar werden mit
gegeben. Die Graphen dieser Schar werden mit  bezeichnet.
bezeichnet.
 und
und  schneiden sich für jedes
schneiden sich für jedes  in einem Punkt.
in einem Punkt.
Begründe, dass die Größe des Schnittwinkels nur von der Steigung des Graphen von im Schnittpunkt abhängt.
im Schnittpunkt abhängt.
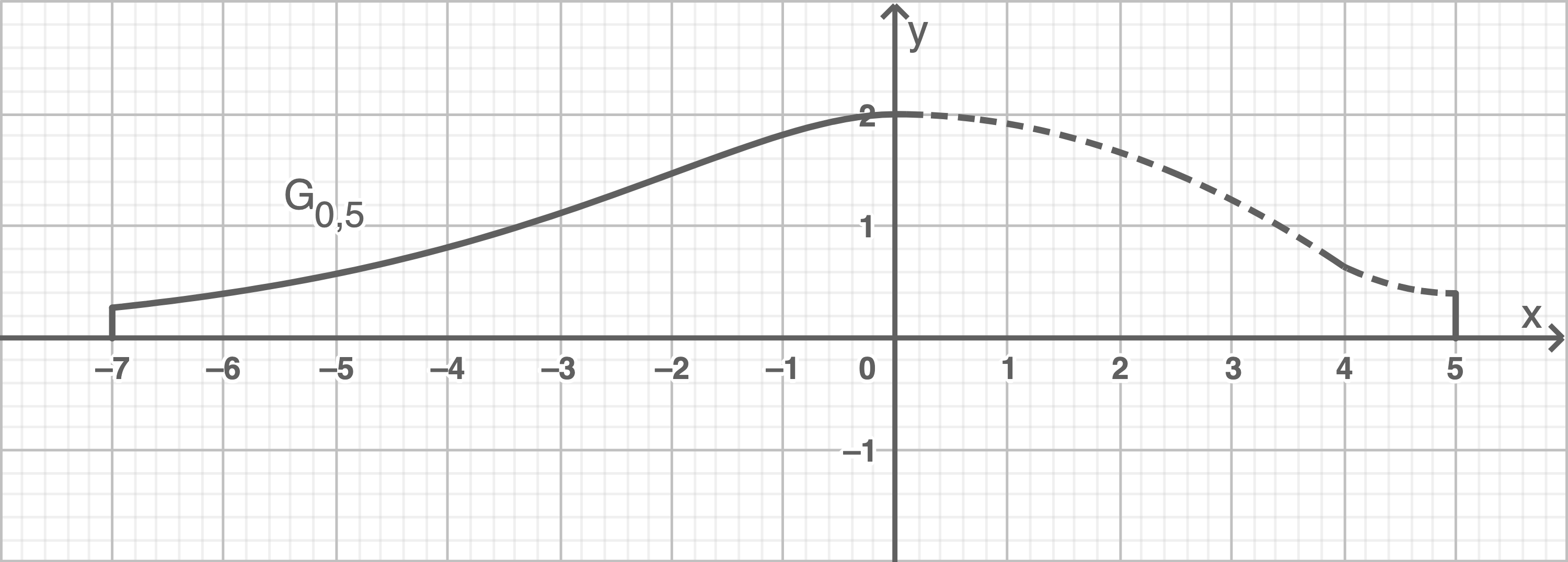
 In einer Trainingshalle für Skiläufer ist eine Skipiste angelegt, auf der kurze Anstiege und Abfahrten trainiert werden können. Das Profil dieser Skipiste wird im Intervall
In einer Trainingshalle für Skiläufer ist eine Skipiste angelegt, auf der kurze Anstiege und Abfahrten trainiert werden können. Das Profil dieser Skipiste wird im Intervall ![\([-7; 0]\)](https://mathjax.schullv.de/c0db0b94c92a2fd15281c31341175226f99450d5336085627c102dfef1a18deb?color=5a5a5a) durch den Graphen der Funktion
durch den Graphen der Funktion  modelliert. In den Intervallen
modelliert. In den Intervallen ![\([0 ; 4]\)](https://mathjax.schullv.de/dc7ed58466b8cc32faff3d38abc9163860a2f00ecfa18f356740e4f25aaa933f?color=5a5a5a) und
und ![\([4;5]\)](https://mathjax.schullv.de/94432a836aa553fce525d68934473bc28f4889cd3d0c30faf76ccea3fa26cd30?color=5a5a5a) erfolgt die Modellierung der Profilkurve durch zwei quadratische Parabeln. Dabei werden die Parabeln so gewählt, dass die Profilkurve keinen Knick hat. Der Boden der Trainingshalle wird in der gleichen Profilansicht durch die
erfolgt die Modellierung der Profilkurve durch zwei quadratische Parabeln. Dabei werden die Parabeln so gewählt, dass die Profilkurve keinen Knick hat. Der Boden der Trainingshalle wird in der gleichen Profilansicht durch die  -Achse beschrieben. In der Abbildung 3 ist die Profilkurve der Skipiste skizziert. Es gilt:
-Achse beschrieben. In der Abbildung 3 ist die Profilkurve der Skipiste skizziert. Es gilt: 
a)
Die Schnittpunkte von  mit den beiden Koordinatenachsen sind
mit den beiden Koordinatenachsen sind  und
und 
Ermittle die Koordinaten dieser beiden Punkte in Abhängigkeit von
Für jeden Wert von sind der Koordinatenursprung
sind der Koordinatenursprung  und die Schnittpunkte
und die Schnittpunkte  und
und  die Eckpunkte eines Dreiecks. Zeige, dass für den Flächeninhalt dieser Dreiecke
die Eckpunkte eines Dreiecks. Zeige, dass für den Flächeninhalt dieser Dreiecke  gilt.
gilt.
Ermittle die Koordinaten dieser beiden Punkte in Abhängigkeit von
Für jeden Wert von
(5 BE)
b)
Gib das Verhalten der Funktionswerte von  für
für  und
und  an.
an.
(2 BE)
c)
Weise nach, dass die Ableitungsfunktionen  von
von  die Gleichung
die Gleichung
 haben.
haben.
Begründe ohne weitere Berechnungen, dass alle Stellen, an denen eine Funktion monoton fallend ist, in einem zusammenhängenden Intervall liegen.
monoton fallend ist, in einem zusammenhängenden Intervall liegen.
Begründe ohne weitere Berechnungen, dass alle Stellen, an denen eine Funktion
(4 BE)
d)
Jeder Graph  hat genau einen Extrempunkt
hat genau einen Extrempunkt 
Zeige, dass dieser Extrempunkt die -Koordinate
-Koordinate  hat und berechne die zugehörige
hat und berechne die zugehörige  -Koordinate.
-Koordinate.
Zeige, dass dieser Extrempunkt die
(3 BE)
e)
Neben dem Extrempunkt  hat jeder Graph
hat jeder Graph  auch genau einen Wendepunkt
auch genau einen Wendepunkt  Zeige, dass der Abstand der
Zeige, dass der Abstand der  -Koordinaten von Extrempunkt und Wendepunkt stets gleich groß ist.
-Koordinaten von Extrempunkt und Wendepunkt stets gleich groß ist.
(6 BE)
f)
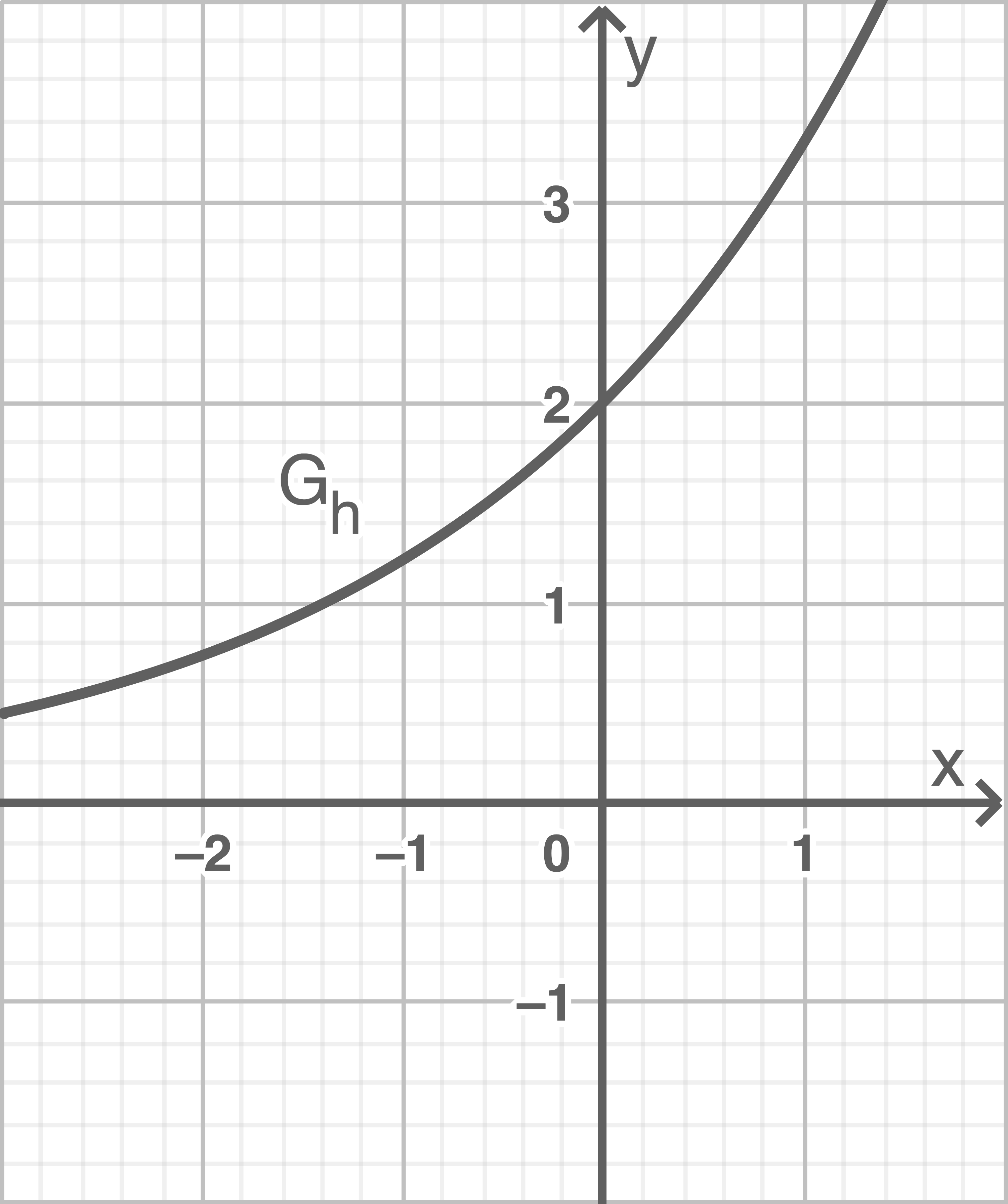
Die Extrempunkte  aller Graphen
aller Graphen  liegen auf dem Graphen einer Funktion
liegen auf dem Graphen einer Funktion  Der Graph
Der Graph  ist in der Abbildung 1 dargestellt.
ist in der Abbildung 1 dargestellt.
Zeige, dass diese Funktion die Gleichung
die Gleichung  hat.
hat.
Zeige, dass diese Funktion

Abb. 1
(2 BE)
g)
Begründe, dass die Größe des Schnittwinkels nur von der Steigung des Graphen von
(3 BE)
h)
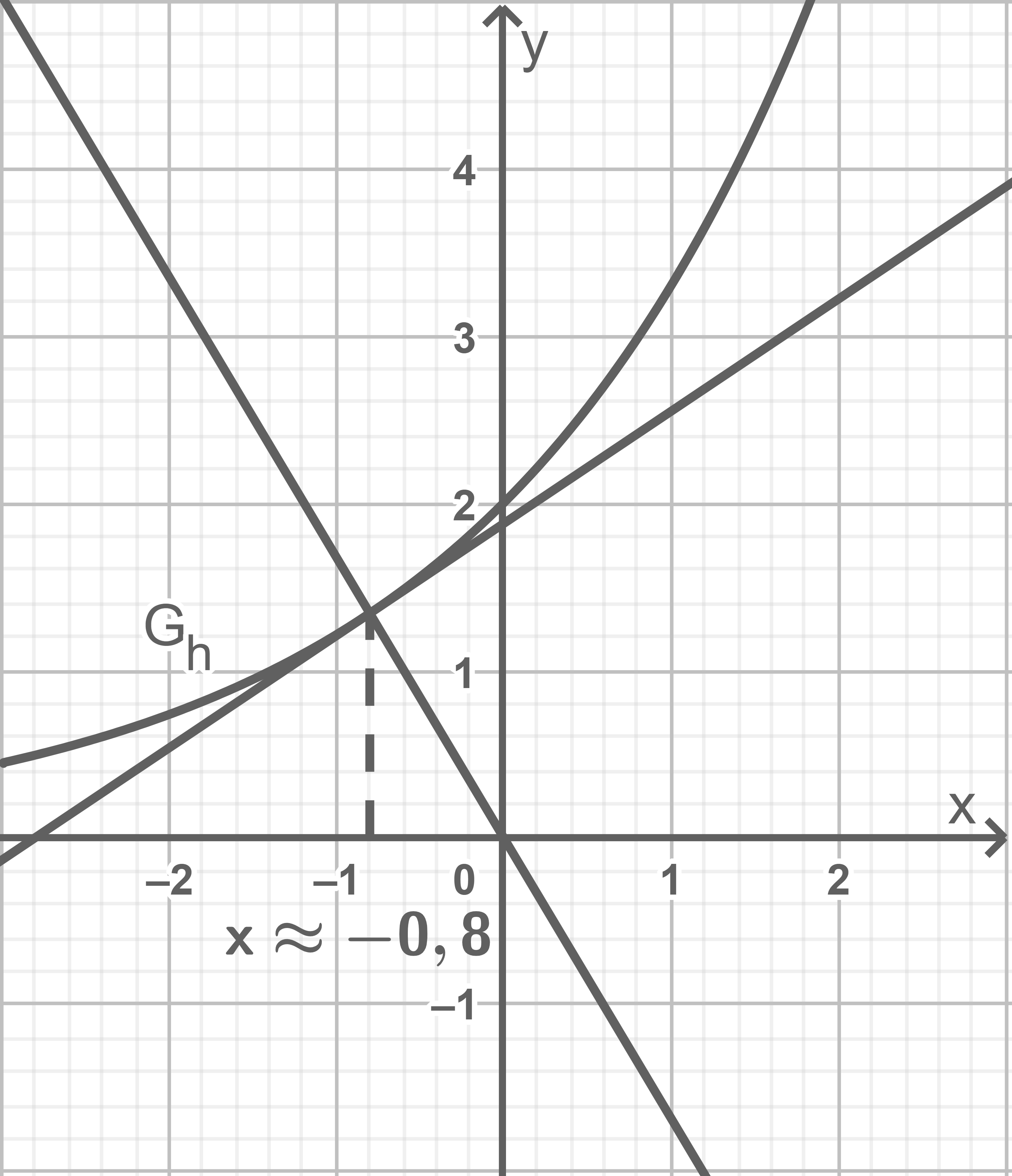
Erläutere, wie unter Zuhilfenahme der Abbildung 1 aus Teilaufgabe  näherungsweise der Parameterwert
näherungsweise der Parameterwert  bestimmt werden kann, für den der zugehörige Extrempunkt zum Koordinatenursprung den kleinsten Abstand hat. Gib einen solchen Näherungswert an.
bestimmt werden kann, für den der zugehörige Extrempunkt zum Koordinatenursprung den kleinsten Abstand hat. Gib einen solchen Näherungswert an.
(5 BE)
i)
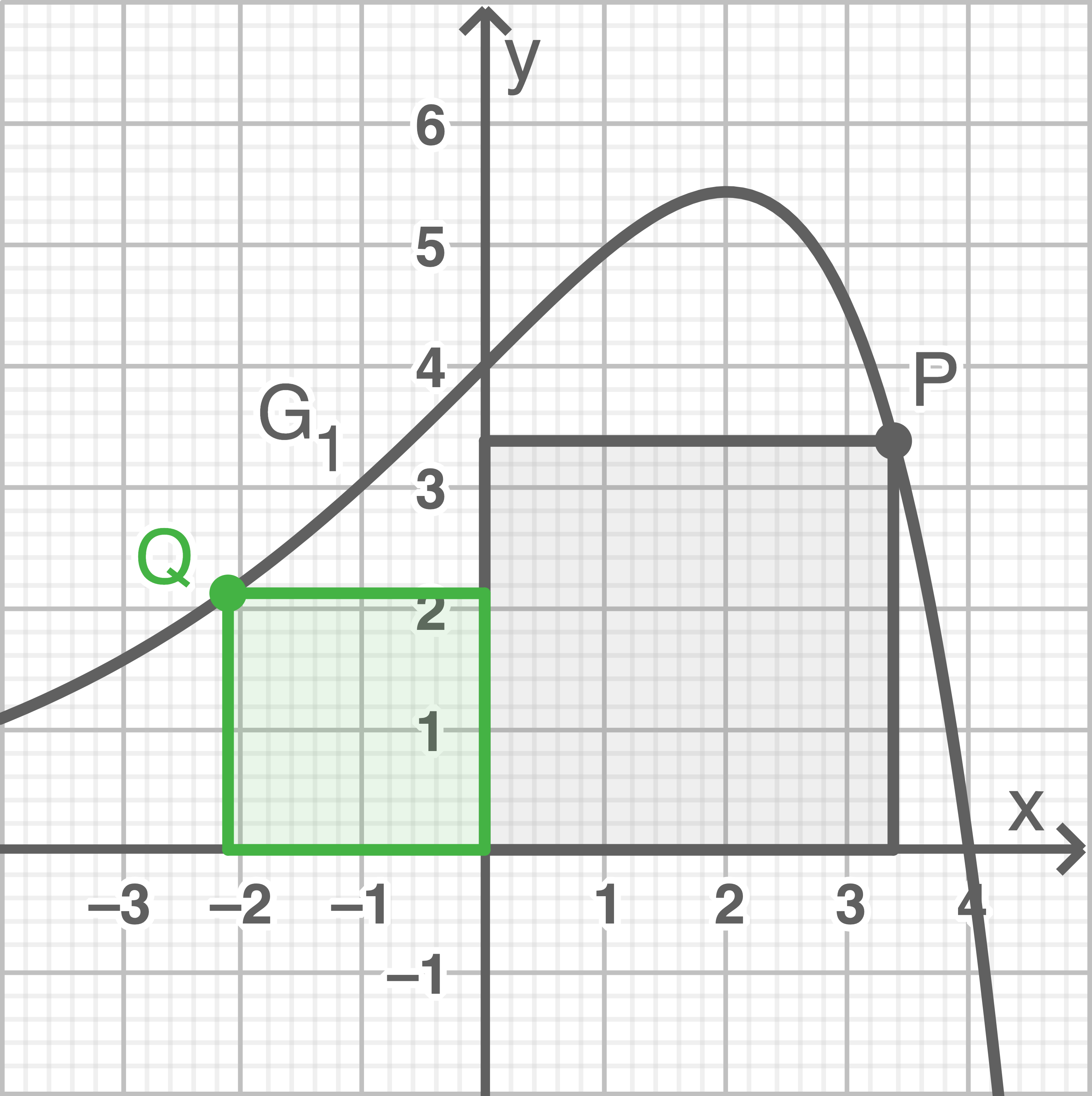
In Abbildung 2 ist der Graph  der Funktion
der Funktion  dargestellt. Auf
dargestellt. Auf  gibt es im I. Quadranten einen Punkt
gibt es im I. Quadranten einen Punkt  , für den gilt:
, für den gilt:  und der Koordinatenursprung
und der Koordinatenursprung  sind die diagonal gegenüberliegenden Eckpunkte eines achsenparallelen Quadrats. Im II. Quadranten gibt es einen Punkt
sind die diagonal gegenüberliegenden Eckpunkte eines achsenparallelen Quadrats. Im II. Quadranten gibt es einen Punkt  auf
auf  . Der Punkt
. Der Punkt  und
und  sind diagonal gegenüberliegende Eckpunkte eines weiteren achsenparallelen Quadrats. Skizziere diese beiden Quadrate in die Abbildung 2 ein. Gib die Gleichungen an, die zu lösen sind, um die Seitenlängen der Quadrate rechnerisch zu bestimmen. Beschreibe, wie man das Verhältnis der Umfänge der beiden Quadrate zueinander berechnen kann.
sind diagonal gegenüberliegende Eckpunkte eines weiteren achsenparallelen Quadrats. Skizziere diese beiden Quadrate in die Abbildung 2 ein. Gib die Gleichungen an, die zu lösen sind, um die Seitenlängen der Quadrate rechnerisch zu bestimmen. Beschreibe, wie man das Verhältnis der Umfänge der beiden Quadrate zueinander berechnen kann.

Abb. 2
(5 BE)

Abb. 3
j)
Ein Skiläufer trainiert auf dem Streckenabschnitt, der durch  modelliert wird. Berechne den Höhenunterschied in Metern über dem Intervall
modelliert wird. Berechne den Höhenunterschied in Metern über dem Intervall ![\([-7 ; 0].\)](https://mathjax.schullv.de/35ff1c9e31592055be4377d9f41031f4a4e7ff7f4f6db914e19ea9ab35b758fe?color=5a5a5a)
(2 BE)
k)
Zeige, dass die Funktion  mit
mit  eine Stammfunktion von
eine Stammfunktion von  ist. Berechne die Größe der Querschnittsfläche der Skipiste im Intervall
ist. Berechne die Größe der Querschnittsfläche der Skipiste im Intervall ![\([-7 ; 0]\)](https://mathjax.schullv.de/4ce74289d35a1ed8b8397d6427f309a40e308a7eb91dc1ec1aab697474796b3a?color=5a5a5a) und gib diese in Quadratmetern an.
und gib diese in Quadratmetern an.
(5 BE)
l)
Begründe, dass die Modellierung der Profilkurve im Intervall ![\([0 ; 5]\)](https://mathjax.schullv.de/b02ee8a49528deae083b74aa0bf199d81e4798d6295a9282cc9cee3ab23f33ff?color=5a5a5a) nicht mit einer quadratischen Parabel anstelle von zwei quadratischen Parabeln möglich ist.
nicht mit einer quadratischen Parabel anstelle von zwei quadratischen Parabeln möglich ist.
(3 BE)
m)
Begründe, dass die Profilkurve der Skipiste im Intervall ![\([0 ; 4]\)](https://mathjax.schullv.de/dc7ed58466b8cc32faff3d38abc9163860a2f00ecfa18f356740e4f25aaa933f?color=5a5a5a) durch eine Parabel mit der Gleichung
durch eine Parabel mit der Gleichung  modelliert werden kann. Berechne die Werte für
modelliert werden kann. Berechne die Werte für  und
und  unter der Bedingung, dass die Querschnittsfläche für den Teil der Wand im Intervall
unter der Bedingung, dass die Querschnittsfläche für den Teil der Wand im Intervall ![\([0 ; 4]\)](https://mathjax.schullv.de/dc7ed58466b8cc32faff3d38abc9163860a2f00ecfa18f356740e4f25aaa933f?color=5a5a5a) eine Größe von
eine Größe von  hat.
hat.
(5 BE)
(50 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Koordinaten der Schnittpunkte ermitteln
 Da
Da  für jedes
für jedes  gilt, muss nach dem Satz des Nullprodukts
gilt, muss nach dem Satz des Nullprodukts  sein, woraus
sein, woraus  folgt. Somit gilt
folgt. Somit gilt 

 Die Koordinaten des Schnittpunkts von
Die Koordinaten des Schnittpunkts von  mit der
mit der  -Achse sind also
-Achse sind also  Flächeninhalt des Dreiecks bestimmen
Flächeninhalt des Dreiecks bestimmen



b)
Für  gilt
gilt  Für
Für  wird der Term
wird der Term  negativ und es folgt
negativ und es folgt  Für
Für  gilt
gilt  und es folgt
und es folgt  Für
Für  wird der Term
wird der Term  positiv und es folgt
positiv und es folgt  Für
Für  strebt der Exponentialterm
strebt der Exponentialterm  gegen Null, während der Term
gegen Null, während der Term  für
für  negativ wird.
Somit gilt
negativ wird.
Somit gilt 
c)
Nachweis der Ableitungsfunktionen
Mit der Produktregel folgt:
Monotonieverhalten begründen
Der Term für die erste Ableitung wird negativ, wenn der lineare Term in der Klammer negativ ist, denn  ist immer positiv. Jede lineare Funktion mit einer Steigung
ist immer positiv. Jede lineare Funktion mit einer Steigung  hat in einem zusammenhängenden Intervall negative Funktionswerte. Also ist für dieses Intervall
hat in einem zusammenhängenden Intervall negative Funktionswerte. Also ist für dieses Intervall  das heißt die Funktion
das heißt die Funktion  verläuft monoton fallend.
verläuft monoton fallend.
d)
e)
1. Schritt: Zweite Ableitung bestimmen
Mit der Produktregel folgt:
2. Schritt: Notwendige Bedingung
 Da
Da  für alle
für alle  gilt, gilt nach dem Satz vom Nullprodukt genau dann
gilt, gilt nach dem Satz vom Nullprodukt genau dann  wenn
wenn 
 Es folgt:
Da nach Aufgabenstellung jeder Graph genau einen Wendepunkt
Es folgt:
Da nach Aufgabenstellung jeder Graph genau einen Wendepunkt  hat, ist
hat, ist  die Wendestelle. Für den Abstand der
die Wendestelle. Für den Abstand der  -Koordinaten von Extrem- und Wendepunkt gilt unabhängig von
-Koordinaten von Extrem- und Wendepunkt gilt unabhängig von 
![\(d=|(4 a-2)-(4 a-4)|=2\;[\text{LE}]\)](https://mathjax.schullv.de/0f6749ac9e6c59dd189547f74823ec3b464bfcc080258501da7d381ec861b4f6?color=5a5a5a)
f)
g)
Für jedes  ist der Extrempunkt
ist der Extrempunkt  der Schnittpunkt zwischen
der Schnittpunkt zwischen  und
und  , da die Extrempunkte
, da die Extrempunkte  von
von  auf
auf  liegen. Da der Graph
liegen. Da der Graph  im Extrempunkt
im Extrempunkt  eine Tangente mit der Steigung
eine Tangente mit der Steigung  besitzt, hängt die Größe des Schnittwinkels nur von der Steigung des Graphen von
besitzt, hängt die Größe des Schnittwinkels nur von der Steigung des Graphen von  im Schnittpunkt
im Schnittpunkt  ab.
ab.
h)
Damit der zu einem Wert von  zugehörige Extrempunkt den kleinsten Abstand zum Koordinatenursprung hat, muss die in diesem Punkt angelegte Ursprungsgerade den Graphen
zugehörige Extrempunkt den kleinsten Abstand zum Koordinatenursprung hat, muss die in diesem Punkt angelegte Ursprungsgerade den Graphen  unter einem Winkel von
unter einem Winkel von  schneiden. Einzeichnen dieser liefert
schneiden. Einzeichnen dieser liefert  Es folgt:
Es folgt:
![\(\begin{array}[t]{rll}
4a-2&=&-0,8 &\quad \scriptsize \mid\;+2 \\[5pt]
4a&=&1,2 &\quad \scriptsize \mid\;:4 \\[5pt]
a&=&0,3
\end{array}\)](https://mathjax.schullv.de/413a90edc39583ec755ae3963e4190297b07e9e111ba0d06bd8db27e58d62308?color=5a5a5a)
i)
Auflösen der Gleichungen 
 bzw.
bzw. 
 mit
mit  liefert die Seitenlängen
liefert die Seitenlängen  bzw.
bzw.  der Quadrate.
Bei zwei Quadraten ist das Verhältnis der Umfänge gleich dem Verhältnis der Seitenlängen, somit liefert der Quotient
der Quadrate.
Bei zwei Quadraten ist das Verhältnis der Umfänge gleich dem Verhältnis der Seitenlängen, somit liefert der Quotient  das gesuchte Verhältnis der Umfänge der beiden Quadrate.
das gesuchte Verhältnis der Umfänge der beiden Quadrate.
j)
k)
Stammfunktion zeigen
Mit der Produktregel folgt:
Querschnittsfläche berechnen
Aus  folgt
folgt  somit hat die Querschnittsfläche der Skipiste im Intervall
somit hat die Querschnittsfläche der Skipiste im Intervall ![\([-7;0]\)](https://mathjax.schullv.de/b04f34580df3e00ba596e0cd2f189450715bfacf1cbab2bd29bae88adbd68ecc?color=5a5a5a) eine Größe von ca.
eine Größe von ca. ![\(7,3 \cdot 25 \approx 183\;[\text{m}^2].\)](https://mathjax.schullv.de/e29f9887538f26e4befc7e552c15aee4411f48d1ee68343f938c5dd68e46d9a0?color=5a5a5a)
l)
Da die Profilkurve bei  und
und  eine waagerechte Tangente besitzt, muss im Intervall
eine waagerechte Tangente besitzt, muss im Intervall ![\([0;5]\)](https://mathjax.schullv.de/9f1084a89e870442044301e496fd2d816c5fe06bded7c4819987d07b5dcf3070?color=5a5a5a) ein Wechsel von einer Rechtskrümmung zu einer Linkskrümmung erfolgen. Mit lediglich einer quadratischen Parabel ist dies nicht möglich.
ein Wechsel von einer Rechtskrümmung zu einer Linkskrümmung erfolgen. Mit lediglich einer quadratischen Parabel ist dies nicht möglich.
m)
Aus der Abbildung folgt, dass die Änderung der Rechtskrümmung in eine Linkskrümmung an der Stelle  erfolgt, somit kann die Skipiste im Intervall
erfolgt, somit kann die Skipiste im Intervall ![\([0;4]\)](https://mathjax.schullv.de/1560f98ba45b1bf50e4254268fc3492c704d99f31b7a236afb4a70174b7d628e?color=5a5a5a) durch eine Parabel mit der Gleichung
durch eine Parabel mit der Gleichung 
 modelliert werden. Dafür muss der Scheitelpunkt die Koordinaten
modelliert werden. Dafür muss der Scheitelpunkt die Koordinaten  haben:
haben:
![\(\begin{array}[t]{rll}
y(0)&=&2 \\[5pt]
a\cdot 0^2+b\cdot 0+c&=&2 \\[5pt]
c&=&2
\end{array}\)](https://mathjax.schullv.de/a7850c5baf832f82b474cfbb8df5c04c67ecedd9da788121581f944c601e406e?color=5a5a5a) Für die Ableitung der Parabel gilt
Für die Ableitung der Parabel gilt 

![\(\begin{array}[t]{rll}
y](https://mathjax.schullv.de/c0ec82ff828fd807cdbb9609baae08158cdd59432cd54cec30792d2f608623a0?color=5a5a5a) Somit folgt
Somit folgt  und
und  Mit
Mit  ergibt sich dann für
ergibt sich dann für 
![\(\begin{array}[t]{rll}
25\cdot \displaystyle\int_0^4(a x^2+2)\mathrm dx&=&155 &\quad \scriptsize \\[5pt]
25\cdot \left[\dfrac{1}{3} a x^3+2 x\right]_0^4&=&155 &\quad \scriptsize \\[5pt]
25\cdot (\dfrac{64}{3} a+8)&=&155 &\quad \scriptsize \mid\; :25\\[5pt]
\dfrac{64}{3} a+8&=&\dfrac{155}{25} &\quad \scriptsize \mid\;-8 \\[5pt]
\dfrac{64}{3} a&=&-\dfrac{9}{5} &\quad \scriptsize \mid\;:\dfrac{64}{3} \\[5pt]
a&=& -\dfrac{27}{320}
\end{array}\)](https://mathjax.schullv.de/a6d2fd968376ba232cd6be4c3fb8eb1df2d73b275b0481955ce3c675e9d919b3?color=5a5a5a) Somit ergeben sich die Werte
Somit ergeben sich die Werte  und
und 