Hilfsmittelfreier Teil

1.1

Analysis

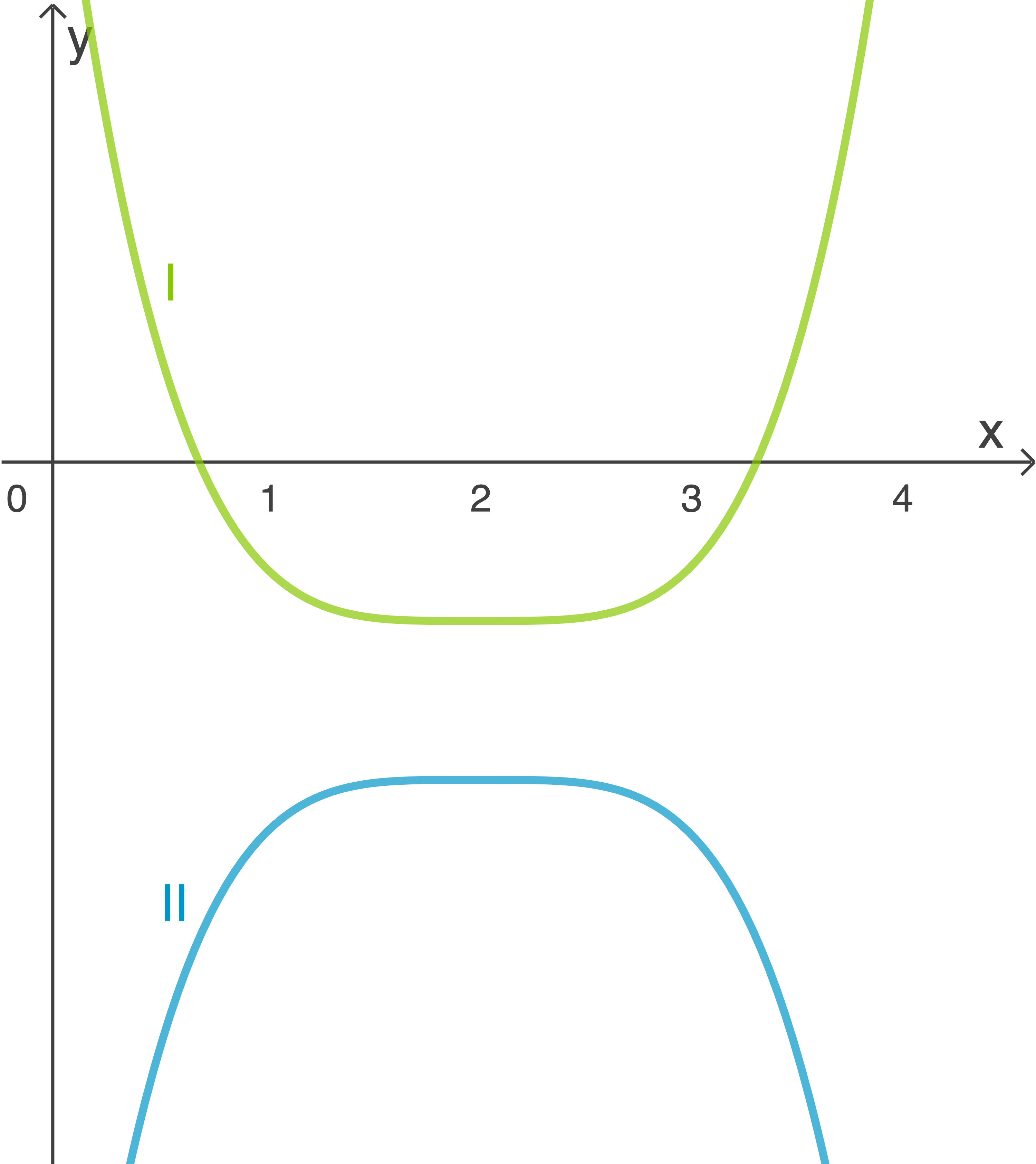
Die Abbildung zeigt den Graphen der Funktion $f$ mit $f(x)=x\cdot e^{-x}$ und $x \in \mathbb{R}$ .

Betrachtet werden die Dreiecke mit den Eckpunkten $O(0\mid 0)$ , $P(a\mid 0)$ und $Q(a\mid f(a))$ mit $a \in \mathbb{R^+}$ .

Graph einer mathematischen Funktion mit x- und y-Achse, dargestellt in grün.

Begründe, dass der Flächeninhalt jedes dieser Dreiecke mit dem Term $\dfrac{1}{2}a^2 e^{-a}$ bestimmt werden kann.

(2 BE)

Unter den betrachteten Dreiecken hat eines den größten Flächeninhalt.
Bestimme den zugehörigen Wert von $a$ .

(3 BE)

1.2

Analysis

Für jeden Wert von $a \in \mathbb{R}\setminus\{ 0\}$ ist eine Funktion $f_a$ gegeben mit

$f_a(x)=a\cdot(x-2)^3$ und $x \in \mathbb{R}$ .

Zeige, dass die in $\mathbb{R}$ definierte Funktion $F$ mit

$F(x)=\dfrac{1}{2}\cdot(x-2)^4+3$

eine Stammfunktion von $f_2$ ist.

(1 BE)

Untersuche mithilfe von Skizzen, für welche Werte von $a$ sich unter den Stammfunktionen von $f_a$ solche befinden, die nur negative Funktionswerte haben.

(4 BE)

1.3

Analytische Geometrie

In einem kartesischen Koordinatensystem sind der Punkt $C(2\mid 3\mid 3)$ und die Gerade $g$ mit

$g:\overrightarrow{x}=\pmatrix{6\\3\\-1}+\mu\cdot \pmatrix{1\\1\\0}$ ; $\mu\in\mathbb{R}$ gegeben.

Die Gerade $g$ verläuft durch die Punkte $A(6\mid 3\mid -1)$ und $B$ .

Zeige, dass der Punkt $C$ nicht auf $g$ liegt.

(2 BE)

Bestimme die Koordinaten des Punktes $B$ , der auf $g$ liegt und gleich weit wie der Punkt $A$ von $C$ entfernt ist.

(3 BE)

1.4

Analytische Geometrie

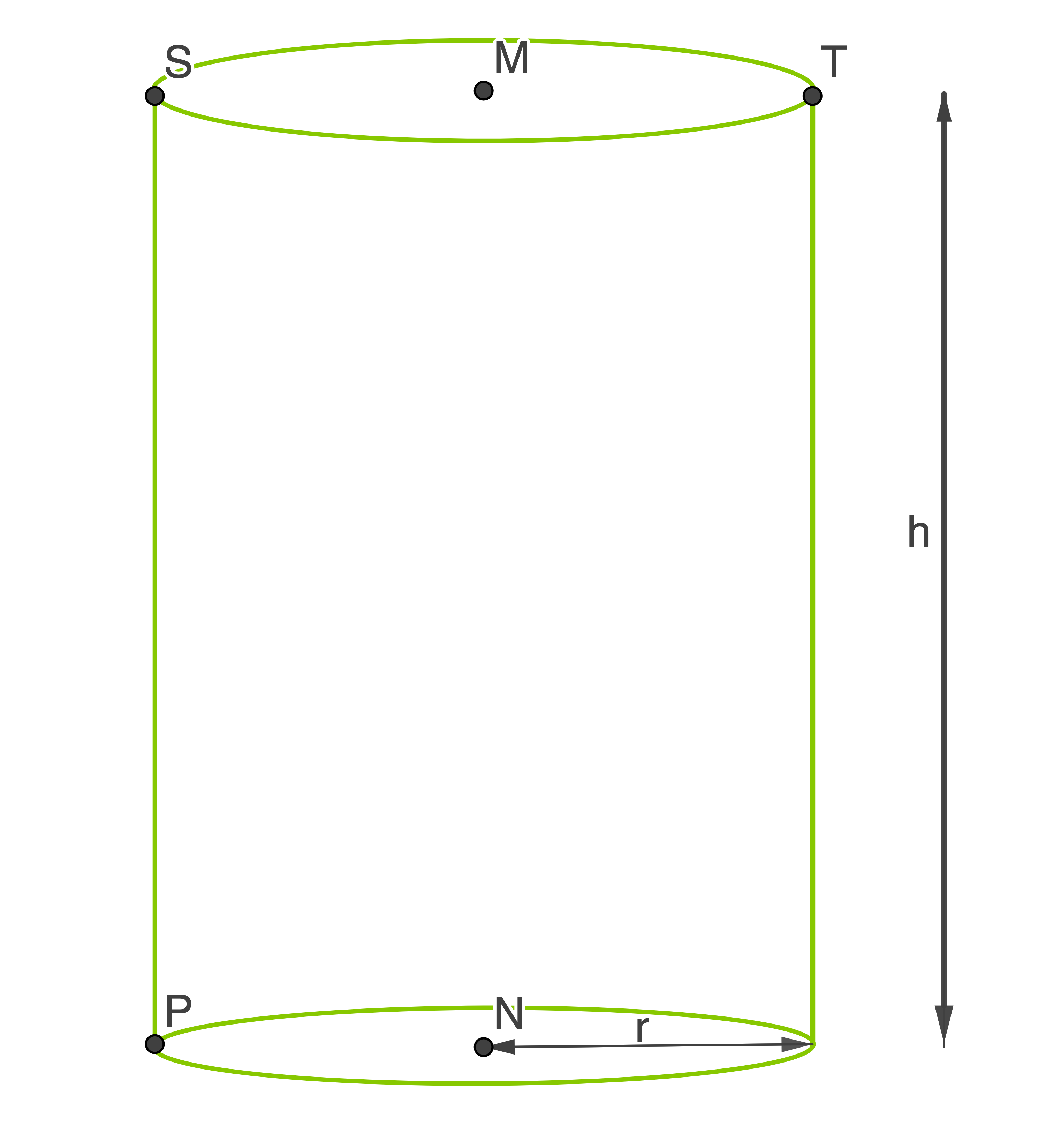
In einem Koordinatensystem ist ein gerader Zylinder mit dem Radius $5$ und der Höhe $10$ gegeben, dessen Grundfläche in der $xy$ -Ebene liegt. $M(8\mid 5\mid 10)$ ist der Mittelpunkt der Deckfläche.

Weise nach, dass der Punkt $P(5\mid 1\mid 0)$ auf dem Rand der Grundfläche des Zylinders liegt.

(2 BE)

Unter allen Punkten auf dem Rand der Deckfläche hat der Punkt $S$ den kleinsten Abstand von $P$ , der Punkt $T$ den größten.
Gib die Koordinaten von $S$ an und bestimme die Koordinaten von $T$ .

(3 BE)

1.5

Stochastik

Für ein Spiel werden ein Tetraeder und ein Würfel verwendet. Die Seiten des Tetraeders sind mit den Zahlen $1$ bis $4$ durchnummeriert, die des Würfels mit den Zahlen $1$ bis $6$ . Ebenso wie beim Werfen des Würfels werden beim Werfen des Tetraeders alle Zahlen mit gleicher Wahrscheinlichkeit erzielt.

Vor Beginn des Spiels wird ein Einsatz von $5$ Euro geleistet. Anschließend wird das Tetraeder einmal geworfen. Wird dabei die Zahl $3$ erziehlt, wird das Tetraeder ein weiteres Mal geworfen, andernfalls einmal der Würfel. Nur dann, wenn bei genau einem der beiden Würfe die Zahl $3$ erzielt wird, erfolgt eine Auszahlung.

Zeige, dass die Wahrscheinlichkeit dafür, bei einmaliger Durchführung des Spiels mindestens einmal die Zahl $3$ zu erzielen, $\dfrac{3}{8}$ beträgt.

(2 BE)

Bei vielfacher Durchführung des Spiels ist zu erwarten, dass sich die Einsätze und Auszahlungen mit der Zeit ausgleichen.
Ermittle die Höhe der Auszahlung.

(3 BE)

1.6

Stochastik

Eine Gärtnerei, die Tulpen in den Farben Gelb, Orange und Rot züchtet, stellt Sträuße mit jeweils $15$ Tulpen zusammen.

Einer der Sträuße soll Tulpen in zwei verschiedenen Farben enthalten. Die Anzahl der Möglichkeiten, diesen Strauß zusammenzustellen, kann mit dem Term $\pmatrix{3\\2}\cdot 14$ berechnet werden.
Beschreibe für jeden der beiden Faktoren die Bedeutung im Sachzusammenhang.

(2 BE)

In einem der Sträuße sollen zu jeder der drei Farben mindestens vier und höchstens sechs Tulpen enthalten sein.
Bestimme die Anzahl der Möglichkeiten, diesen Strauß zusammenzustellen.

(3 BE)

(30 BE)

Lösung 1.1 Analysis

Term für den Flächeninhalt der Dreiecke in Abhängigkeit von $a$ bestimmen:

$A_{\text{Dreieck}}=\dfrac{1}{2} \cdot \text{Grundseite}\cdot \text{Höhe}$

$\begin{array}[t]{rll} A_{\text{Dreieck}_{OPQ}}&=&\dfrac{1}{2} \cdot a \cdot f(a) &\quad \\[5pt] &=&\dfrac{1}{2} \cdot a \cdot a\cdot \mathrm{e}^{-a} &\quad \\[5pt] &=&\dfrac{1}{2} \cdot a^2\cdot \mathrm{e}^{-a} &\quad \\[5pt] \end{array}$

Daraus folgt, dass mit dem Term $\dfrac{1}{2} \cdot a^2\cdot \mathrm{e}^{-a}$ der Flächeninhalt jedes dieser Dreiecke bestimmt werden kann.

Wert von $a$ bestimmen, sodass der Flächeninhalt des jeweiligen Dreiecks maximal ist:

Definiere $A(a)=\dfrac{1}{2} \cdot a^2\cdot \mathrm{e}^{-a}$ , $\, a\in\mathbb{R}^+$ .

Der größte Flächeninhalt in Abhängigkeit von $a$ entspricht dem Maximum von $A$ .
Wende das notwendige Kriterium für Extremstellen an.

$\( A$

Vollständige Lösung anzeigen

$\(A$ , daraus folgt $\dfrac{1}{2}a\cdot \mathrm{e}^{-a}(2-a)=0$

Mit dem Satz vom Nullprodukt gilt:
$\dfrac{1}{2}a=0$ , $\mathrm{e}^{-a}=0$ oder $2-a=0$

Die Lösung $a=0$ liegt nicht im Definitionsbereich für $a$ .
$\mathrm e^{-a}=0$ besitzt keine Lösung.
Für $a=2$ ist der Flächeninhalt des zugehörigen Dreiecks maximal.

Lösung 1.2 Analysis

$f_2(x)=2\cdot(x-2)^3$

Behauptung: $F (x)=\dfrac{1}{2}\cdot(x-2)^4+3$ ist eine Stammfunktion von $f_2$ .

Ableiten der Funktion $F$ mittels Kettenregel:

$\(\begin{array}[t]{rll} F$

Daraus folgt, dass $F (x)=\dfrac{1}{2}\cdot(x-2)^4+3$ eine Stammfunktion von $f_2$ darstellt.

Term für alle Stammfunktionen aufstellen:

$F_{a,c}(x)= \dfrac{a}{4}\cdot(x-2)^4+c , c \in\mathbb{R}$

Skizze erstellen:

Für $a\gt0$ besitzt $F_{a,c}(x)= \dfrac{a}{4}\cdot(x-2)^4+c$ stets Funktionswerte, die positiv sind (siehe Graph I).

Für $a\lt0$ gibt es stets Werte von $c$ , sodass $F_{a,c}(x)= \dfrac{a}{4}\cdot(x-2)^4+c$ ausschließlich negative Funktionswerte besitzt (siehe Graph II).

Graph mit zwei Kurven in verschiedenen Farben, dargestellt in einem Koordinatensystem.

Lösung 1.3 Analytische Gemometrie

Punktprobe mit dem Punkt $C(2|3|3)$ auf der Geraden $g$ durchführen:

$\pmatrix{2\\3\\3}= \pmatrix{6\\3\\-1}+\mu\cdot\pmatrix{1\\1\\0}$

Aus der ersten Zeile folgt:

$\begin{array}[t]{rll} 2&=& 6+\mu&\quad \scriptsize \mid\; -6\\[5pt] -4&=& \mu \end{array}$

Aus der zweiten Zeile folgt:

$\begin{array}[t]{rll} 3&=& 3+\mu&\quad \scriptsize \mid\;-3 \\[5pt] 0&=& \mu \end{array}$

Aus der dritten Zeile folgt:

$\begin{array}[t]{rll} 3&\neq& -1 \end{array}$

Die Werte für den Parameter $\mu$ stimmen nicht überein.
Damit ist gezeigt, dass der Punkt $C$ nicht auf der Geraden $g$ liegt.

Koordinaten des Punktes $B$ bestimmen:

Bilde eine Hilfsebene $H$ durch den Punkt $C$ mit dem Richtungsvektor der Geraden $g$ als Normalenvektor $n=\pmatrix{1\\1\\0}$ .

$\begin{array}[t]{rll} H:x+y&=& 5 \end{array}$

Berechne die Koordinaten des Schnittpunktes $S$ der Ebene $H$ mit der Geraden $g$ .

$\begin{array}[t]{rll} 6+\mu+3+\mu&=& 5& \\[5pt] 9+2\mu&=& 5& \quad \scriptsize \mid\;-9\\[5pt] 2\mu&=& -4& \quad \scriptsize \mid\;:2\\[5pt] \mu&=& -2& \end{array}$

$\begin{array}[t]{rll} \overrightarrow{OS}&=& \pmatrix{6\\3\\-1}+ (-2)\cdot\pmatrix{1\\1\\0} \\[5pt] &=& \pmatrix{4\\1\\-1} \\[5pt] \end{array}$

Die Koordinaten des Schnittpunktes $S$ lauten $S(4|1|-1)$ .

Für den Punkt $B$ gilt: $\begin{array}[t]{rll} \overrightarrow{OB}&=& \overrightarrow{OA}+2\cdot\overrightarrow{AS} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{AS} &=& \pmatrix{-2\\-2\\0}\\[5pt] \end{array}$

$\begin{array}[t]{rll} \overrightarrow{OB} &=& \pmatrix{6\\3\\-1}+2\cdot\pmatrix{-2\\-2\\0} \\[5pt] &=& \pmatrix{6-4\\3-4\\-1+0}&\\[5pt] &=&\pmatrix{2\\-1\\-1}& \end{array}$

Die Koordinaten des Punktes $B$ lauten $B(2|-1|-1)$ .

Lösung 1.4 Analytische Geometrie

Diagramm eines Zylinders mit Beschriftungen für Höhe und Radius.

(Die Skizze ist nicht maßstabsgetreu.)

Lage des Punktes $P$ untersuchen:

Der Punkt $P$ befindet sich in der $xy$ -Ebene.

$\begin{array}[t]{rll} \overrightarrow{ON}&=& \overrightarrow{OM}-\pmatrix{0\\0\\10}& \\[5pt] &=& \pmatrix{8\\5\\10}-\pmatrix{0\\0\\10}& \\[5pt] &=& \pmatrix{8\\5\\0} \end{array}$

Berechne den Abstand zwischen den Punkten $N(8|5|0)$ (Mittelpunkt der Grundfläche) und $P(5|1|0)$ .

$\begin{array}[t]{rll} \mid\overrightarrow{NP}\mid&=&\left|\pmatrix{5-8\\1-5\\0-0}\right|& \\[5pt] &=& \bigg\vert\pmatrix{-3\\-4\\0}\bigg\vert&\\[5pt] &=& \sqrt{(-3)^2+(-4)^2+0^2}& \\[5pt] &=& 5\,[LE] \end{array}$

Damit ist gezeigt, dass der Punkt $P(5|1|0)$ auf dem Rand der Grundfläche des Zylinders liegt.

Die Koordinaten von den Punkten $S$ und $T$ bestimmen:

Der Punkt $S$ liegt auf dem Rand der Deckfläche und hat den kleinsten Abstand zum Punkt $P$ . $\begin{array}[t]{rll} \overrightarrow{OS}&=& \overrightarrow{OP}+\pmatrix{0\\0\\10}&\\[5pt] &=& \pmatrix{5\\1\\10}& \end{array}$

Koordinaten des Punktes $S$ : $S(5|1|10)$

Der Punkt $T$ liegt ebenfalls auf dem Rand der Deckfläche und hat den größten Abstand zum Punkt $P$ .

$\begin{array}[t]{rll} \overrightarrow{OT}&=& \overrightarrow{OM}+\overrightarrow{SM} \\[5pt] &=& \pmatrix{8\\5\\10}+\pmatrix{3\\4\\0}\\[5pt] &=& \pmatrix{11\\9\\10} \end{array}$

Koordinaten des Punktes $T$ : $T(11|9|10)$

Lösung 1.5 Stochastik

Wahrscheinlichkeit berechnen:

Ereignis $A$ : mindestens einmal die Zahl $3$ erzielen
Ereignis $B$ : keinmal die Zahl $3$ erzielen

$\begin{array}[t]{rll} P(B)&=&\dfrac{3}{4}\cdot \dfrac{5}{6} &\quad \\[5pt] &=&\dfrac{15}{24} \end{array}$

$\begin{array}[t]{rll} P(A)&=&1-P(B) &\quad \\[5pt] &=&1- \dfrac{15}{24}&\quad \\[5pt] &=&\dfrac{3}{8} \end{array}$

Die Wahrscheinlichkeit, bei einmaliger Durchführung des Spiels mindestens einmal die Zahl $3$ zu erzielen, beträgt $\dfrac{3}{8}$ .

Höhe der Auszahlung $a$ bestimmen:

Es muss $E(X)=5\,€$ gelten, sodass sich die Einsätze und Auszahlungen mit der Zeit ausgleichen.

$\begin{array}[t]{rll} E(X)&=&5\,€&\quad \\[5pt] \left(\dfrac{3}{8}-\dfrac{1}{4}\cdot \dfrac{1}{4}\right)\cdot a &=&5\,€ &\quad \\[5pt] \dfrac{5}{16}\cdot a &=&5\,€&\quad \scriptsize \mid\; \cdot \dfrac{16}{5}\\[5pt] a&=&16\,€&\quad \\[5pt] \end{array}$

Die Höhe der Auszahlung muss $16\,€$ betragen, sodass sich die Einsätze und Auszahlungen mit der Zeit ausgleichen.

Lösung 1.6 Stochastik

Bedeutung des Terms erläutern:

Die Anzahl der Möglichkeiten, dass ein Strauß aus Tulpen zwei verschiedene Farben enthält, kann mit dem Term $\pmatrix{3\\2}\cdot 14$ beschrieben werden.

Der erste Faktor (Binomialkoeffizient) gibt die Anzahl der Möglichkeiten an, zwei der drei Farben auszuwählen.
Der zweite Faktor ( $14$ ) beschreibt die Anzahl der Möglichkeiten für die Anzahl der Tulpen in einer der beiden Farben.

Anzahl der Möglichkeiten bestimmen:

Es gibt verschiedene Möglichkeiten, die Anforderung an den Blumenstrauß zu erfüllen:

Blumenstrauß aus jeweils $5$ Tulpen der drei Farben
Blumenstrauß aus $4$ Tulpen der ersten Farbe, $5$ Tulpen der zweiten Farbe und $6$ Tulpen der dritten Farbe

Für die $1.$ gibt es genau eine Möglichkeit. Für die $2.$ wiederum sechs Möglichkeiten die Tulpen anzuordnen.
Insgesamt gibt es also sieben verschiedene Möglichkeiten, den Strauß zusammenzustellen.