Analysis 2.1 - Eingangstor
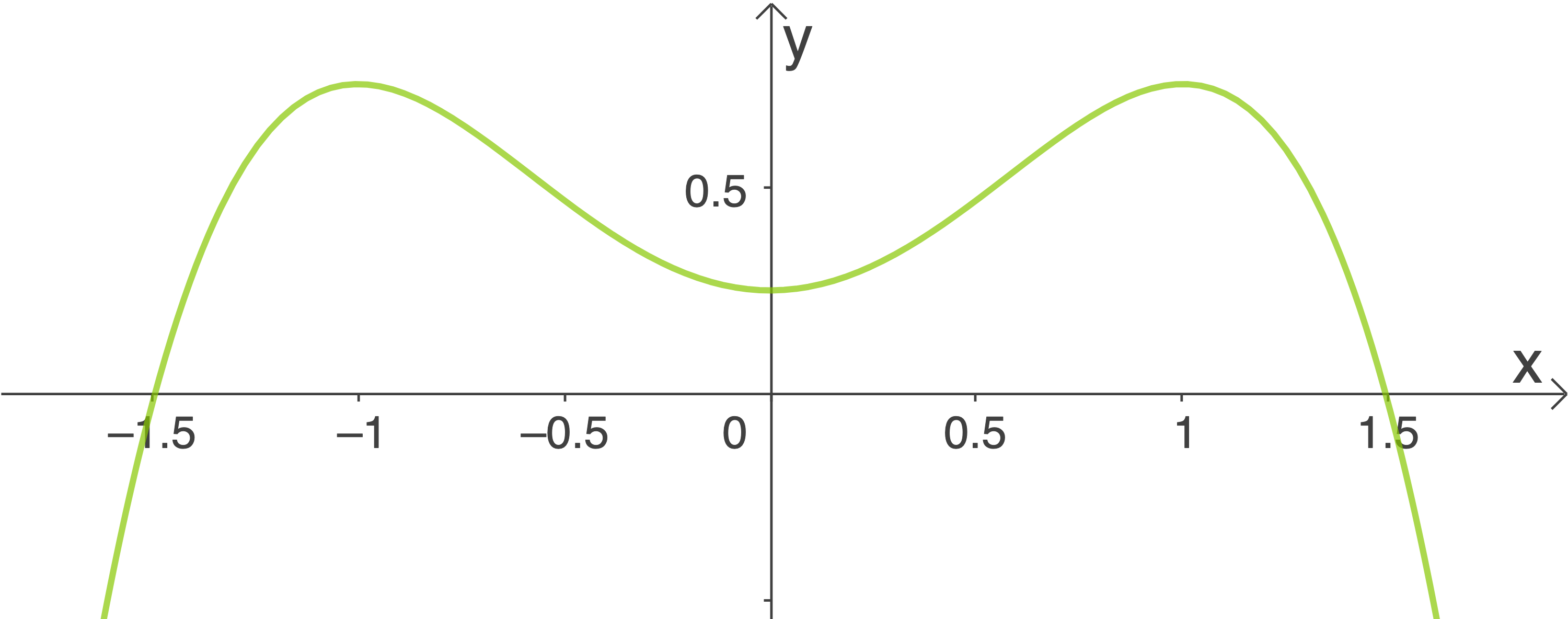
Gegeben ist die Funktionenschar  mit der Gleichung
mit der Gleichung  ;
; 
Die zugehörigen Graphen sind .
.
Die zugehörigen Graphen sind
a)
Zeige, dass alle Graphen  achsensymmetrisch zur
achsensymmetrisch zur  -Achse verlaufen.
-Achse verlaufen.
(1 BE)
b)
Gib das Verhalten von  für
für  in Anhängigkeit von
in Anhängigkeit von  an.
an.
(4 BE)
c)
Bestimme rechnerisch für den Graphen der Funktion  die Koordinaten und die Art der lokalen Extrempunkte.
die Koordinaten und die Art der lokalen Extrempunkte.
(9 BE)
d)
Gib den Schnittpunkt  aller Graphen
aller Graphen  mit der
mit der  -Achse an.
-Achse an.
Weise nach, dass dieser stets lokaler Tiefpunkt ist. [Kontrollergebnis: ]
]
Weise nach, dass dieser stets lokaler Tiefpunkt ist. [Kontrollergebnis:
(5 BE)
e)
Gib die Anzahl der Nullstellen von  in Anhängigkeit von
in Anhängigkeit von  an und begründe diese anhand der in a) bis d) ermittelten Eigenschaften.
In der Abbildung 1 ist der Graph
an und begründe diese anhand der in a) bis d) ermittelten Eigenschaften.
In der Abbildung 1 ist der Graph  dargestellt.
dargestellt.
(5 BE)
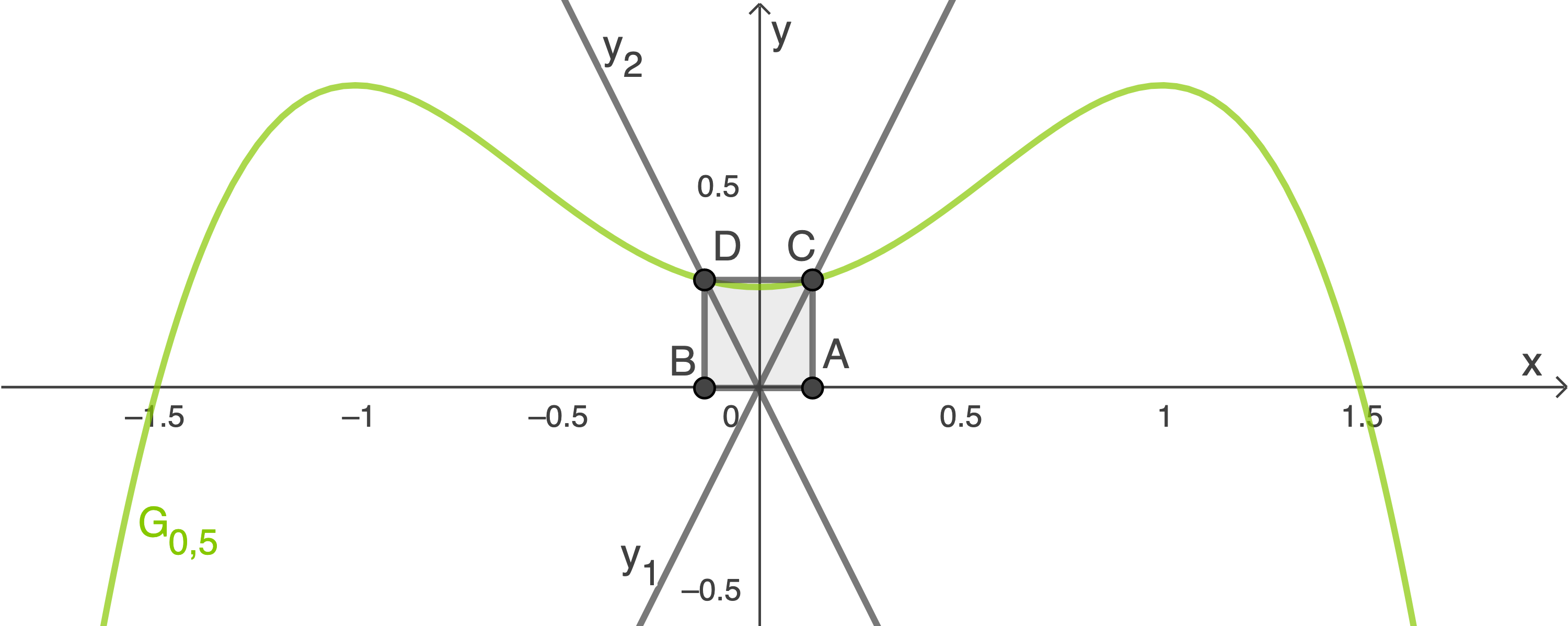
f)
Begründe unter Zuhilfenahme der Abbildung 1, dass es ein zur  -Achse symmetrisches Quadrat geben muss, von dem zwei Eckpunkte auf der
-Achse symmetrisches Quadrat geben muss, von dem zwei Eckpunkte auf der  -Achse und zwei Eckpunkte auf
-Achse und zwei Eckpunkte auf  liegen.
liegen.
(3 BE)
g)
Ein Punkt auf dem Graphen  im ersten Quadranten und der Koordinatenursprung sind die diagonal gegenüberliegenden Eckpunkte eines achsenparallelen Rechtecks.
im ersten Quadranten und der Koordinatenursprung sind die diagonal gegenüberliegenden Eckpunkte eines achsenparallelen Rechtecks.
Die waagerechte Rechteckseite ist lang. Der Graph
lang. Der Graph  teilt dieses Rechteck in zwei Teilflächen.
Ermittle das Verhältnis der Flächeninhalte dieser Teilflächen.
teilt dieses Rechteck in zwei Teilflächen.
Ermittle das Verhältnis der Flächeninhalte dieser Teilflächen.
Hinweis: Runde die Ergebnisse auf 2 Dezimalstellen.
Die waagerechte Rechteckseite ist
Hinweis: Runde die Ergebnisse auf 2 Dezimalstellen.
(5 BE)
h)
Die Tangente  im Punkt
im Punkt  an den Graphen
an den Graphen  und die Senkrechte zur Tangente
und die Senkrechte zur Tangente  im Punkt
im Punkt  schließen mit der
schließen mit der  -Achse ein Dreieck ein.
-Achse ein Dreieck ein.
Ermittle einen Parameterwert so, dass das Dreieck gleichschenklig ist und die Basis auf der
so, dass das Dreieck gleichschenklig ist und die Basis auf der  -Achse liegt.
-Achse liegt.
Ermittle einen Parameterwert
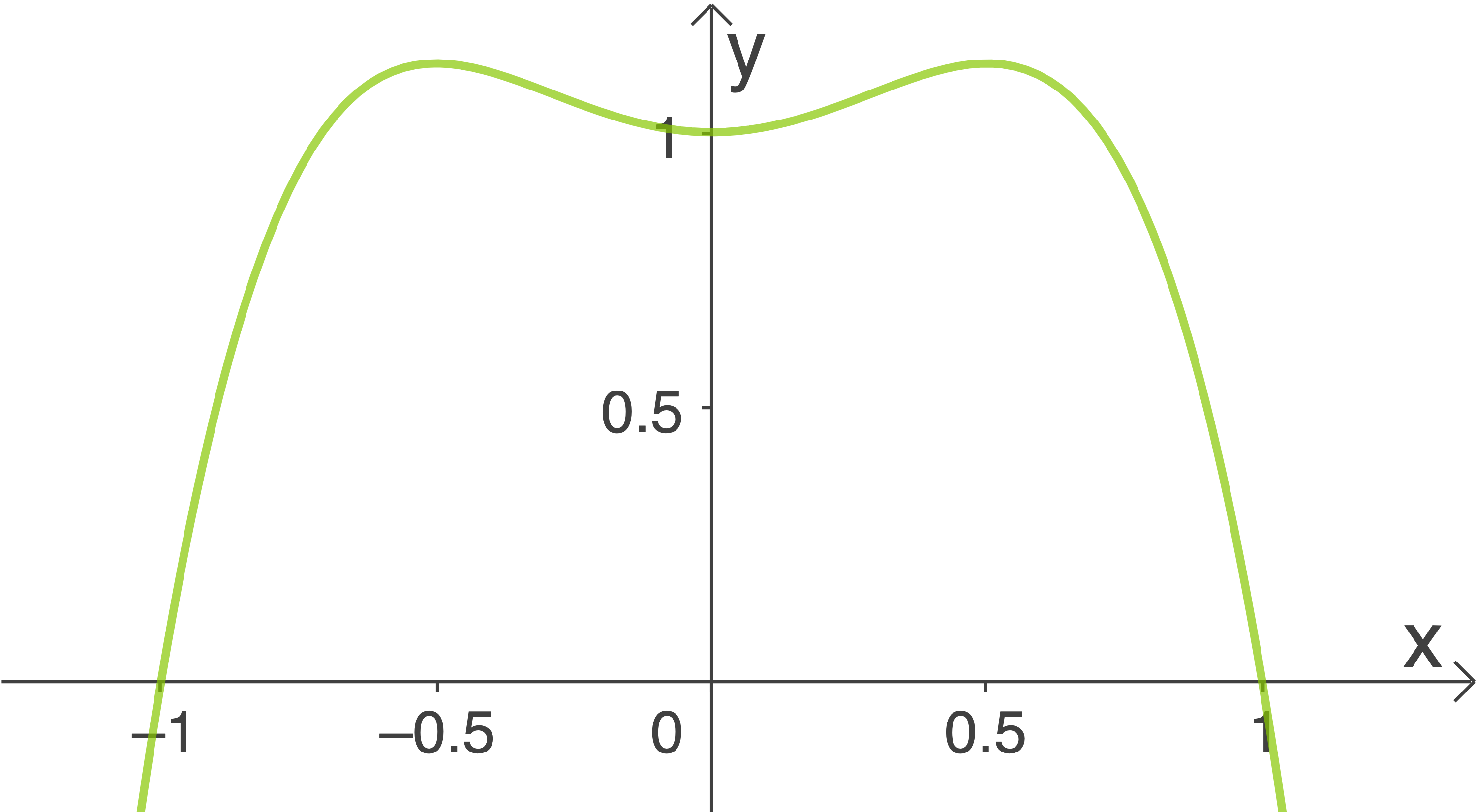
Für die folgende Teilaufgabe wird die Funktion  mit
mit
 ;
;  betrachtet. Der Graph
betrachtet. Der Graph  beschreibt im Inervall
beschreibt im Inervall ![\([-1;1]\)](https://mathjax.schullv.de/73fceed2b3adf84dcb76747f17cc4310d1fdbead831740568456586cf877554d?color=5a5a5a) die Profillinie für das Eingangstor eines Vergnügungsparks (siehe Abbildung 2). Die
die Profillinie für das Eingangstor eines Vergnügungsparks (siehe Abbildung 2). Die  -Achse stellt im Profil die untere Begrenzung dar.
-Achse stellt im Profil die untere Begrenzung dar.
Es gilt:
Es gilt:
(4 BE)
i)
Ermittle, welche Breite ein Fahrzeug mit einem quaderförmigen Aufbau unterschreiten muss, damit es bei Ausnutzung der maximalen Durchfahrtshöhe gerade noch mittig das Eingangstor passieren kann.
(4 BE)
(40 BE)
a)
Graphen  auf Achsensymmetrie zur
auf Achsensymmetrie zur  -Achse überprüfen:
-Achse überprüfen:
Achsensymmetrisch zur -Achse bedeutet:
-Achse bedeutet: 
![\(\begin{array}[t]{rll}
f_a(-x)&=&-a(-x)^4+(-x)^2+\dfrac{a}{2} &\quad \\[5pt]
&=&-ax^4+x^2+\dfrac{a}{2} &\quad \\[5pt]
&=&f_a(x)
\end{array}\)](https://mathjax.schullv.de/c9d6f6628aa603168d937e92b0c9ef1989a3d8298dde8ee822f93bfd7fb9be32?color=5a5a5a) Dadurch ist gezeigt, dass die Graphen
Dadurch ist gezeigt, dass die Graphen  achsensymmetrisch zur
achsensymmetrisch zur  -Achse verlaufen.
-Achse verlaufen.
Achsensymmetrisch zur
b)
Grenzwerte bestimmen:
Für gilt:
gilt:  Für
Für  gilt:
gilt: 
Für
c)
Koordinaten und Art der lokalen Extrempunkte bestimmen:


 Notwendiges Kriterium:
Notwendiges Kriterium: 
![\(\begin{array}[t]{rll}
-2x^3+2x&=&0 &\quad \\[5pt]
2x\cdot (-x^2+1)&=&0\quad \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9b0d7196dd1faf7ed95c4c2b075f1f4e58218478602a8a8f01071e31b2b7995b?color=5a5a5a) Mit dem Satz vom Nullprodukt gilt:
Mit dem Satz vom Nullprodukt gilt:
 oder
oder 
Daraus folgt: oder
oder 
Hinreichendes Kriterium: , daraus folgt, dass
, daraus folgt, dass  an der Stelle
an der Stelle  ein lokales Maximum besitzt.
ein lokales Maximum besitzt.
 , daraus folgt, dass
, daraus folgt, dass  an der Stelle
an der Stelle  ein lokales Minimum besitzt.
ein lokales Minimum besitzt.
 , daraus folgt, dass
, daraus folgt, dass  an der Stelle
an der Stelle  ein lokales Minimum besitzt.
ein lokales Minimum besitzt.
 , daraus folgt, dass
, daraus folgt, dass  an der Stelle
an der Stelle  ein lokales Maximum besitzt.
ein lokales Maximum besitzt.
 , daraus folgt, dass
, daraus folgt, dass  an der Stelle
an der Stelle  ein lokales Maximum besitzt.
ein lokales Maximum besitzt.
Koordinaten der Extremstellen bestimmen:
 ,
,  und
und 
Daraus folgt:
Hinreichendes Kriterium:
Koordinaten der Extremstellen bestimmen:
d)
Nachweisen, dass  stets ein lokaler Tiefpunkt ist:
stets ein lokaler Tiefpunkt ist:

Koordinaten des Schnittpunktes mit der -Achse:
-Achse: 

 Notwendiges Kriterium:
Notwendiges Kriterium:  für
für  gilt:
gilt: 
Hinreichendes Kriterium: , daraus folgt, dass
, daraus folgt, dass  an der Stelle
an der Stelle  stets ein lokales Minimum besitzt.
stets ein lokales Minimum besitzt.
Damit ist nachgewiesen, dass der Schnittpunkt aller Graphen
aller Graphen  mit der
mit der  -Achse stets ein lokaler Tiefpunkt ist.
-Achse stets ein lokaler Tiefpunkt ist.
Koordinaten des Schnittpunktes mit der
Hinreichendes Kriterium:
Damit ist nachgewiesen, dass der Schnittpunkt
e)
Anzahl der Nullstellen von  in Abhängigkeit von
in Abhängigkeit von  angeben:
angeben:
Fall :
:
Für existiert genau eine Nullstelle, da in diesem Fall die Normalparabel entsteht.
Fall
existiert genau eine Nullstelle, da in diesem Fall die Normalparabel entsteht.
Fall  :
:
Für existieren genau zwei Nullstellen, da der Tiefpunkt (und damit auch die beiden möglichen Hochpunkte) über der
existieren genau zwei Nullstellen, da der Tiefpunkt (und damit auch die beiden möglichen Hochpunkte) über der  -Achse liegt und die Funktionswerte für
-Achse liegt und die Funktionswerte für  gegen
gegen  streben.
Fall
streben.
Fall  :
:
Für existieren ebenfalls genau zwei Nullstellen, da der Tiefpunkt unter der
existieren ebenfalls genau zwei Nullstellen, da der Tiefpunkt unter der  -Achse liegt und somit die Funktionswerte für
-Achse liegt und somit die Funktionswerte für  gegen
gegen  streben.
Hochpunkte kann es nicht geben, weil dann das Verhalten der Funktionswerte von
streben.
Hochpunkte kann es nicht geben, weil dann das Verhalten der Funktionswerte von  für
für  anders sein müsste.
anders sein müsste.
Fall
Für
Für
Für
f)
Quadrat finden:
Gesucht ist ein zur -Achse symmetrisches Quadrat mit der Seitenlänge
-Achse symmetrisches Quadrat mit der Seitenlänge  , von dem zwei Eckpunkte auf der
, von dem zwei Eckpunkte auf der  -Achse und zwei Eckpunkte auf dem Graphen
-Achse und zwei Eckpunkte auf dem Graphen  liegen.
liegen.
Bedingungen, die erfüllt werden müssen:
Für den ersten Eckpunkt auf der -Achse muss gelten:
-Achse muss gelten:  Für den zweiten Eckpunkt auf der
Für den zweiten Eckpunkt auf der  -Achse muss gelten:
-Achse muss gelten:  Für den ersten Eckpunkt auf
Für den ersten Eckpunkt auf  muss gelten:
muss gelten:  und
und  Für den zweiten Eckpunkt auf
Für den zweiten Eckpunkt auf  muss gelten:
muss gelten:  und
und 
Der Eckpunkt liegt im
liegt im  Quadranten auf dem Graphen der Geraden
Quadranten auf dem Graphen der Geraden  , welche einen Schnittpunkt mit dem Graphen
, welche einen Schnittpunkt mit dem Graphen  besitzt.
besitzt.
Aufgrund der Achsensymmetrie des Graphen gibt es im
gibt es im  Quadranten ebenfalls einen Eckpunkt, der auf dem Graphen der Geraden
Quadranten ebenfalls einen Eckpunkt, der auf dem Graphen der Geraden  liegt und einen Schnittpunkt mit dem Graphen
liegt und einen Schnittpunkt mit dem Graphen  besitzt.
besitzt.
Mit dieser Begründung ist bewiesen, dass es ein zur -Achse symmetrisches Quadrat geben muss, von dem zwei Eckpunkte auf der
-Achse symmetrisches Quadrat geben muss, von dem zwei Eckpunkte auf der  -Achse und zwei Eckpunkte auf
-Achse und zwei Eckpunkte auf  liegen.
Skizze:
liegen.
Skizze:
Gesucht ist ein zur
Bedingungen, die erfüllt werden müssen:
Für den ersten Eckpunkt auf der
Der Eckpunkt
Aufgrund der Achsensymmetrie des Graphen
Mit dieser Begründung ist bewiesen, dass es ein zur
g)
Verhältnis der Flächeninhalte der beiden Teilflächen ermitteln:
Eckpunkt des Rechtecks:
Der Eckpunkt des Rechtecks, der auf dem Graphen liegt, hat die Koordinaten
liegt, hat die Koordinaten  .
Flächeninhalt des Rechtecks:
.
Flächeninhalt des Rechtecks:
 Flächeninhalt unterhalb des Graphen:
Flächeninhalt unterhalb des Graphen:
Verhältnis der Flächeninhalte dieser Teilflächen:
Der Graph  teilt die Rechteckfläche im Verhältnis
teilt die Rechteckfläche im Verhältnis  .
.
Eckpunkt des Rechtecks:
Der Eckpunkt des Rechtecks, der auf dem Graphen
Verhältnis der Flächeninhalte dieser Teilflächen:
|
|
h)
Wert für den Paramter  ermitteln:
ermitteln:
 Steigung der Tangenten bestimmen:
Steigung der Tangenten bestimmen:
 Die Tangente und die zugehörige Senkrechte schließen einen rechten Winkel (
Die Tangente und die zugehörige Senkrechte schließen einen rechten Winkel ( ) ein.
) ein.
Das beschriebene Dreieck soll gleichschenklig sein, das heißt, dass die Basiswinkel groß sein müssen.
groß sein müssen.
Damit dies erfüllt ist, müssen die Anstiege der Tangente und der Senkrechte entweder und
und  oder
oder  und
und  sein.
Möglichkeit
sein.
Möglichkeit  :
: 
![\(\begin{array}[t]{rll}
-4a+2&=&1 &\quad \scriptsize \mid\; -2\\[5pt]
-4a&=&1 &\quad \scriptsize \mid\; :(-4)\\[5pt]
a&=&\dfrac{1}{4}
\end{array}\)](https://mathjax.schullv.de/fc20b24f65b8e44d17a861685c2b1ffcfef8d2e26fe4382a2472cc30cc3c3368?color=5a5a5a) Möglichkeit
Möglichkeit  :
: 
![\(\begin{array}[t]{rll}
-4a+2&=&-1 &\quad \scriptsize \mid\; -2\\[5pt]
-4a&=&-3 &\quad \scriptsize \mid\; :(-4)\\[5pt]
a&=&\dfrac{3}{4}
\end{array}\)](https://mathjax.schullv.de/5927c869fcd0dead5f86ca5dd25c41c8e9369f4992a310f57a05d4acba862a7b?color=5a5a5a) Für die Parameterwerte
Für die Parameterwerte  oder
oder  ist das beschriebene Dreieck gleichschenklig.
ist das beschriebene Dreieck gleichschenklig.
Das beschriebene Dreieck soll gleichschenklig sein, das heißt, dass die Basiswinkel
Damit dies erfüllt ist, müssen die Anstiege der Tangente und der Senkrechte entweder
i)
Zu unterschreitende Breite eines Fahrzeuges ermitteln:
Bestimme die Lösung folgender Gleichung:
![\(\begin{array}[t]{rll}
-2x^4+x^2+1&=&1 &\quad \scriptsize \mid\; -1\\[5pt]
-2x^4+x^2&=&0 \\[5pt]
x^2\cdot(-2x^2+1)&=&0
\end{array}\)](https://mathjax.schullv.de/41ba715cb720ccd855a4c865f17014855ca10428c443d35474dbb1be65c5ae78?color=5a5a5a) Mit dem Satz vom Nullprodukt gilt:
Mit dem Satz vom Nullprodukt gilt:
 oder
oder  Daraus ergeben sich die Lösungen
Daraus ergeben sich die Lösungen  ,
,  oder
oder  .
Die Lösungen
.
Die Lösungen  und
und  entfallen.
Die Breite des Fahrzeuges entspricht
entfallen.
Die Breite des Fahrzeuges entspricht  .
Eine Längeneinheit entspricht
.
Eine Längeneinheit entspricht  .
Daraus folgt, dass die Breite des Fahrzeuges den Wert
.
Daraus folgt, dass die Breite des Fahrzeuges den Wert  unterschreiten muss.
unterschreiten muss.
Bestimme die Lösung folgender Gleichung: