Analytische Geometrie 3 - Körper
Die Abbildung zeigt den Körper  mit
mit 



 und
und 
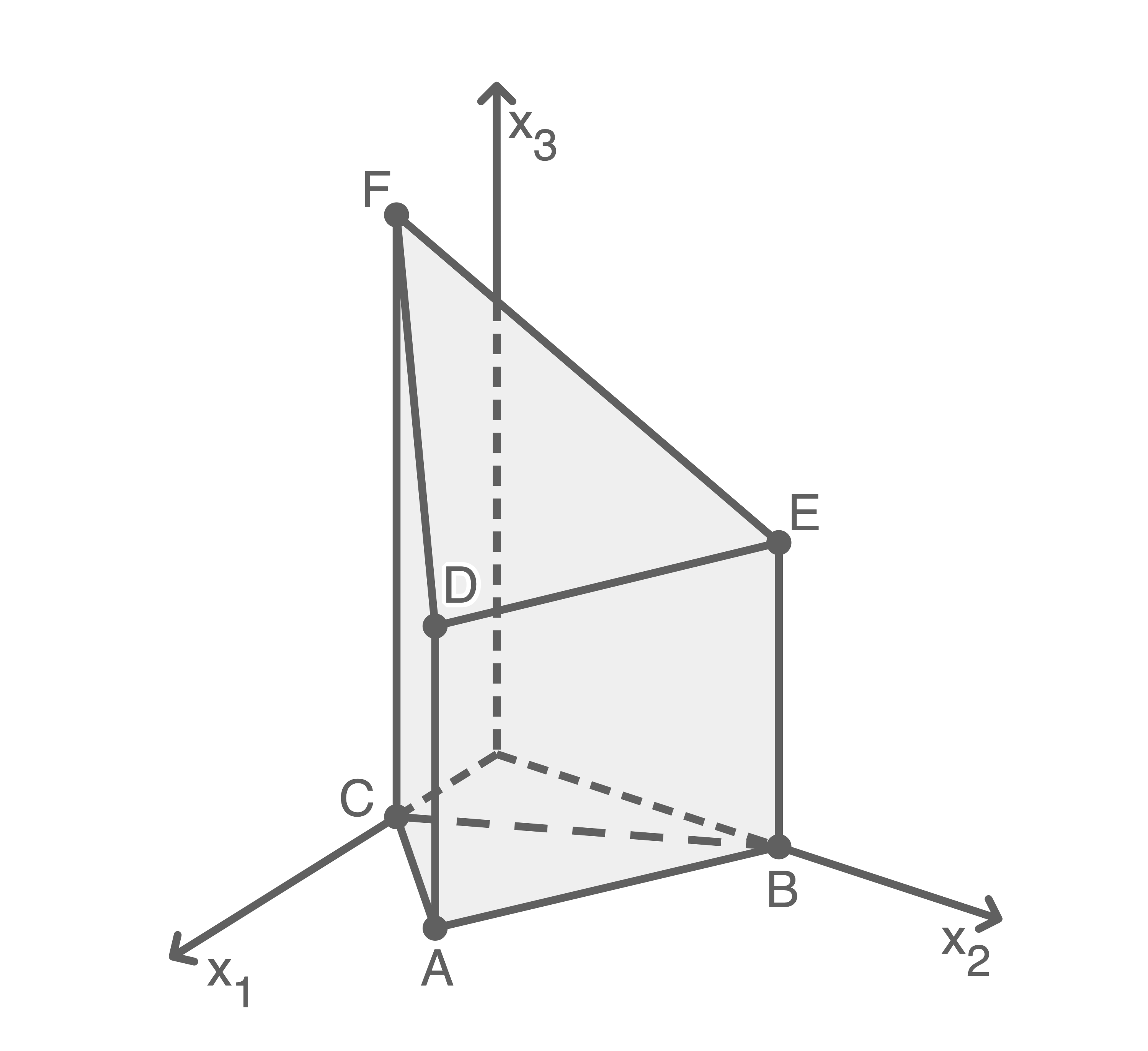
 und der Körper
und der Körper  in seiner ursprünglichen Lage.
in seiner ursprünglichen Lage.
a)
Die Punkte 
 und
und  liegen in der Ebene
liegen in der Ebene  Ermittle eine Gleichung von
Ermittle eine Gleichung von  in Koordinatenform.
in Koordinatenform.
(zur Kontrolle: )
)
(zur Kontrolle:
(4 BE)
b)
Bestimme die Größe des Winkels, den  mit der
mit der  -Ebene einschließt.
-Ebene einschließt.
(3 BE)

c)
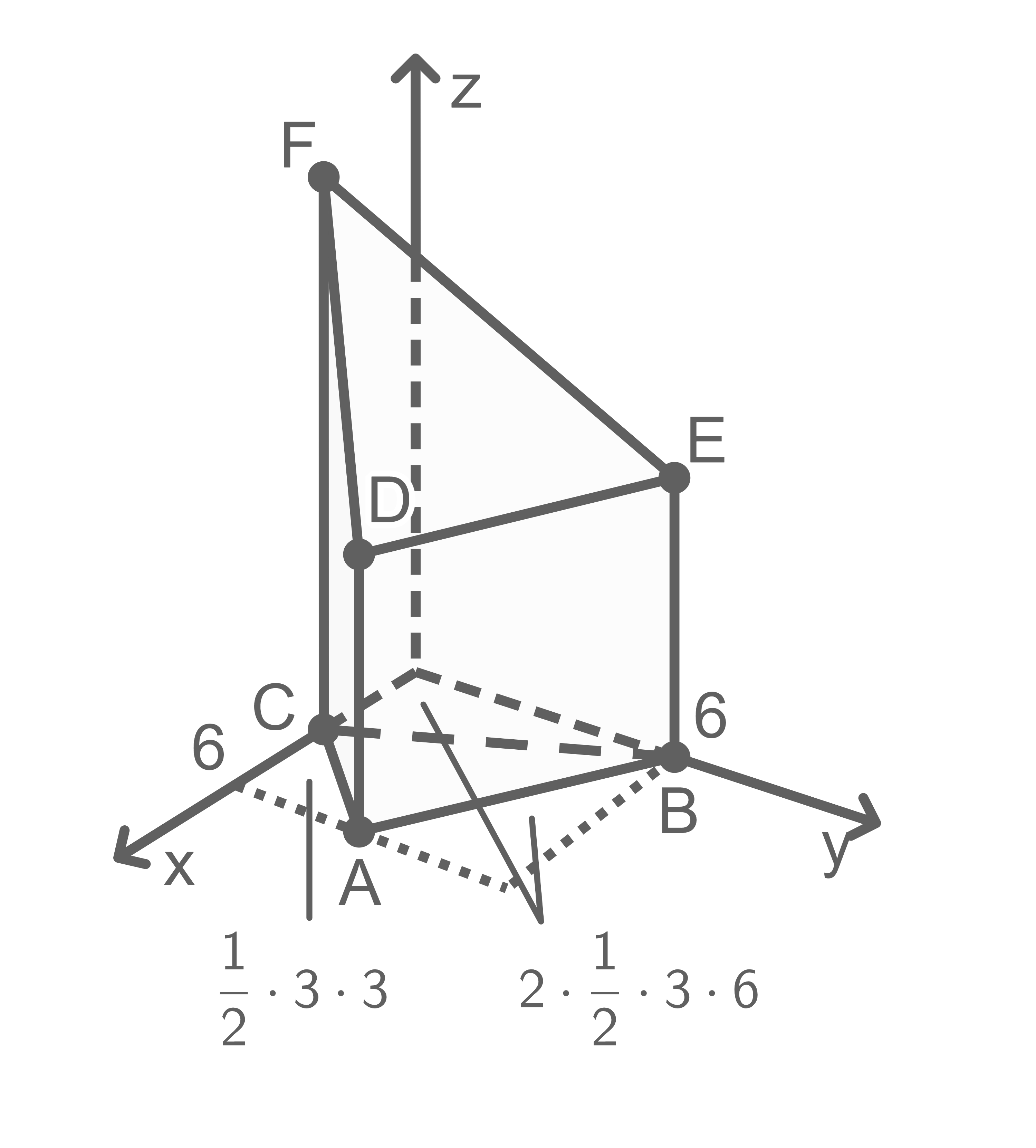
Der Flächeninhalt des Dreiecks  kann mit dem Term
kann mit dem Term  berechnet werden.
berechnet werden.
Veranschauliche diese Tatsache durch geeignete Eintragungen in der Abbildung.
Veranschauliche diese Tatsache durch geeignete Eintragungen in der Abbildung.
(3 BE)
d)
Berechne das Volumen des Körpers 
(3 BE)
e)
Die Gerade  geht durch die Punkte
geht durch die Punkte  und
und  Die Ebene
Die Ebene  enthält die
enthält die  -Achse und einen Punkt
-Achse und einen Punkt  der auf der Geraden
der auf der Geraden  liegt. Der Punkt
liegt. Der Punkt  soll so gewählt werden, dass die Ebene
soll so gewählt werden, dass die Ebene  mit allen vier Kanten
mit allen vier Kanten 


 des Körpers
des Körpers  jeweils einen gemeinsamen Punkt hat.
jeweils einen gemeinsamen Punkt hat.
Ermittle alle Punkte auf der Geraden für die diese Bedingung erfüllt ist.
für die diese Bedingung erfüllt ist.
Ermittle alle Punkte auf der Geraden
(4 BE)
f)
Auf der Kante  liegt der Punkt
liegt der Punkt  , auf der Kante
, auf der Kante  der Punkt
der Punkt  .
.
Das Dreieck hat in
hat in  einen rechten Winkel. Bestimme die
einen rechten Winkel. Bestimme die  -Koordinate von
-Koordinate von 
Das Dreieck
(5 BE)
g)
Der Körper wird so um die Strecke  gedreht, dass die Punkte
gedreht, dass die Punkte  und
und  nach der Drehung in der
nach der Drehung in der  -Ebene liegen und dabei eine positive
-Ebene liegen und dabei eine positive  -Koordinate haben.
-Koordinate haben.
Durch die Drehung wird der Punkt auf den Punkt
auf den Punkt  abgebildet. Die Koordinaten des Punktes
abgebildet. Die Koordinaten des Punktes  sollen bestimmt werden.
sollen bestimmt werden.
Beschreibe einen Lösungsweg zur Bestimmung der Koordinaten von
Betrachtet werden nun die Ebenenschar Durch die Drehung wird der Punkt
Beschreibe einen Lösungsweg zur Bestimmung der Koordinaten von
(5 BE)
h)
Weise nach, dass gilt:
Für einen Wert von liegt die Strecke
liegt die Strecke  in der Ebene
in der Ebene 
Für einen Wert von
(2 BE)
i)
Der Punkt  liegt in der Ebene
liegt in der Ebene  . Die Schnittpunkte der Ebene
. Die Schnittpunkte der Ebene  mit dem Körper
mit dem Körper  sind Eckpunkte eines Dreiecks.
sind Eckpunkte eines Dreiecks.
Ermittle die Koordinaten eines weiteren Eckpunktes dieses Dreiecks.
Ermittle die Koordinaten eines weiteren Eckpunktes dieses Dreiecks.
(2 BE)
j)
Bestimme die Werte des Parameters  für die gilt:
für die gilt:
Der Abstand des Punktes zur Ebene
zur Ebene  beträgt
beträgt 
Der Abstand des Punktes
(5 BE)
k)
Es gibt Werte  , so dass folgende Aussage wahr ist:
, so dass folgende Aussage wahr ist:
Für alle gilt, dass die Ebene
gilt, dass die Ebene  und der Körper
und der Körper  keine gemeinsamen Punkte haben.
keine gemeinsamen Punkte haben.
Gib den kleinstmöglichen Wert von an. Begründe deine Angabe.
an. Begründe deine Angabe.
Für alle
Gib den kleinstmöglichen Wert von
(4 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Ein Normalenvektor von  folgt mit:
folgt mit:
![\(\begin{array}[t]{rll}
\overrightarrow{n}&=& \overrightarrow{DE}\times\overrightarrow{DF} & \\[5pt]
&=& \pmatrix{-6\\3\\0}\times \pmatrix{-3\\-3\\6}& \\[5pt]
&=& \pmatrix{3\cdot 6-(-3)\cdot 0\\0\cdot (-3)-6\cdot (-6)\\(-6)\cdot (-3)-(-3)\cdot 3}& \\[5pt]
&=& \pmatrix{18\\36\\27}& \\[5pt]
&=& 9\cdot \pmatrix{2\\4\\3}
\end{array}\)](https://mathjax.schullv.de/a40e72fff2e15f229a7969edc13c152fad0d0f4a52d6b1536fd3adbd3fd53e73?color=5a5a5a) Einsetzen in die allgemeine Koordinatengleichung:
Einsetzen in die allgemeine Koordinatengleichung:
 Durch Punktprobe mit
Durch Punktprobe mit  folgt:
folgt:
![\(\begin{array}[t]{rll}
2\cdot 6+4\cdot 3+3\cdot 6&=& d& \\[5pt]
42 &=& d
\end{array}\)](https://mathjax.schullv.de/76b007fe448dd2a32ff3583f0a1e4b0398c9bc176d06c4c264478cc6ab5e48b5?color=5a5a5a) Eine Gleichung von
Eine Gleichung von  in Koordinatenform ist somit gegeben durch:
in Koordinatenform ist somit gegeben durch:

b)
Für die Ebene  kann ein Normalenvektor
kann ein Normalenvektor  aus der Koordinatenform abgelesen werden. Als Normalenvektor der
aus der Koordinatenform abgelesen werden. Als Normalenvektor der  -Ebene kann
-Ebene kann  gewählt und somit der Winkel berechnet werden.
gewählt und somit der Winkel berechnet werden.
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\pmatrix{2\\4\\3}\circ \pmatrix{0\\0\\1}}{\sqrt{2^2+4^2+3^2}} \\[5pt]
&=& \dfrac{3}{\sqrt{29}}
\end{array}\)](https://mathjax.schullv.de/c8db6a98e2be3325a39c58151584359646486f4c8a9f76051b24e373e3608cb3?color=5a5a5a) Daraus folgt:
Daraus folgt: 
c)
d)
Flächeninhalt der Grundfläche:
Der Körper kann unterteilt werden in ein dreiseitiges Prisma, dessen Grundfläche das Dreieck  bildet, und eine dreiseitige Pyramide mit der Spitze
bildet, und eine dreiseitige Pyramide mit der Spitze  , welche sich oberhalb des Prismas befindet.
Das Volumen des dreiseitigen Prismas ergibt sich mit:
, welche sich oberhalb des Prismas befindet.
Das Volumen des dreiseitigen Prismas ergibt sich mit:
![\(\begin{array}[t]{rll}
A_{\text{Prisma}}&=& A_{ABC}\cdot h& \\[5pt]
&=& \dfrac{27}{2} \cdot 6& \\[5pt]
&=& 81 \;[\text{VE}]
\end{array}\)](https://mathjax.schullv.de/ec0c7b376c172e70c7f51f6748aa37e28487b3aeed4048ebc7f4fcf8f00fe7e7?color=5a5a5a) Das Volumen der dreiseitigen Pyramide folgt durch:
Das Volumen der dreiseitigen Pyramide folgt durch:
![\(\begin{array}[t]{rll}
A_{\text{Pyramide}}&=& \dfrac{1}{3}\cdot A_{ABC} \cdot h &\\[5pt]
&=& \dfrac{1}{3}\cdot \dfrac{27}{2} \cdot 6 &\\[5pt]
&=& 27 \;[\text{VE}]
\end{array}\)](https://mathjax.schullv.de/7965578131151df00d1eb64b0a112a4205419e80dc2c923c55d800d93344436a?color=5a5a5a) Das Gesamtvolumen des Körpers ist also gegeben durch:
Das Gesamtvolumen des Körpers ist also gegeben durch:
![\(\begin{array}[t]{rll}
A&=& A_{\text{Prisma}}+A_{\text{Pyramide}}& \\[5pt]
&=& 81+27& \\[5pt]
&=& 108 \;[\text{VE}]
\end{array}\)](https://mathjax.schullv.de/448af3e0e5e2d4019cb42f27e72222d9de6d018c802963c616b63a72333b7b6d?color=5a5a5a)
e)
Für die Geradengleichung von  folgt:
folgt:


 Wenn die Gerade, die durch den Ursprung und
Wenn die Gerade, die durch den Ursprung und  verläuft, einen Schnittpunkt mit der Strecke
verläuft, einen Schnittpunkt mit der Strecke  hat, werden die vier Kanten
hat, werden die vier Kanten  und
und  von der Ebene
von der Ebene  geschnitten.
Punkte auf
geschnitten.
Punkte auf  ermitteln, die die Bedingung erfüllen
Da die
ermitteln, die die Bedingung erfüllen
Da die  - und
- und  -Koordinate von
-Koordinate von  jeweils null sind, schneidet die Gerade
jeweils null sind, schneidet die Gerade  die Gerade durch den Ursprung
die Gerade durch den Ursprung  und
und  im Punkt
im Punkt 
Für den Schnittpunkt von mit der Geraden durch
mit der Geraden durch  und
und  folgt:
folgt:


 Aus der ersten Zeile folgt
Aus der ersten Zeile folgt  einsetzen in die zweite Zeile liefert:
einsetzen in die zweite Zeile liefert:
![\(\begin{array}[t]{rll}
-6s+1&=&3s &\quad \scriptsize \mid\;+6s \\[5pt]
1&=&9s &\quad \scriptsize \mid\;:9 \\[5pt]
\dfrac{1}{9}&=&s
\end{array}\)](https://mathjax.schullv.de/7a8d46c859710bd61600d7cbf86d50bdde7589bd33ebe13098c15b8844cf362e?color=5a5a5a) Der Schnittpunkt hat damit die Koordinaten
Der Schnittpunkt hat damit die Koordinaten 
Alle Punkte der Geraden die zwischen
die zwischen  und
und  liegen, erfüllen damit die Bedingung.
liegen, erfüllen damit die Bedingung.
Für den Schnittpunkt von
Alle Punkte der Geraden
f)
Sei  die gesuchte
die gesuchte  -Koordinate von
-Koordinate von  , dann gilt:
Da
, dann gilt:
Da  auf der Kante
auf der Kante  liegt, kommt für die
liegt, kommt für die  -Koordinate nur
-Koordinate nur  infrage.
infrage.
g)
Der Punkt  liegt senkrecht über einem Punkt
liegt senkrecht über einem Punkt  , der auf der Strecke
, der auf der Strecke  liegt. Dabei ist
liegt. Dabei ist  der Lotfußpunkt von
der Lotfußpunkt von  auf die Gerade durch die Punkte
auf die Gerade durch die Punkte  und
und  . Zunächst muss
. Zunächst muss  ermittelt werden. Danach wird der Abstand der Punkte
ermittelt werden. Danach wird der Abstand der Punkte  und
und  berechnet. Die
berechnet. Die  - und
- und  -Koordinate des Punktes
-Koordinate des Punktes  ergeben sich aus denen von
ergeben sich aus denen von  . Die
. Die  -Koordinate von
-Koordinate von  hat den Wert des Abstands der Punkte
hat den Wert des Abstands der Punkte  und
und  .
.
h)
Einsetzen der Koordinaten von  und
und  in die Ebenengleichung der Schar
in die Ebenengleichung der Schar  liefert:
liefert:









 Somit liegt die Strecke
Somit liegt die Strecke  für
für  in
in 
i)
Einsetzen der Koordinaten eines allgemeinen Punktes von beispielsweise der Strecke  in die Ebenengleichung von
in die Ebenengleichung von  liefert:
liefert:
![\(\begin{array}[t]{rll}
6+0+2t&=&15 &\quad \scriptsize \mid\;-6 \\[5pt]
2t&=&9 &\quad \scriptsize \mid\;:2 \\[5pt]
t&=&4,5
\end{array}\)](https://mathjax.schullv.de/2457b5e7e599a5328f2e8a18ba7365c635afa8d82bbc1873728c875f51ade045?color=5a5a5a) Da
Da  gilt, liegt der Schnittpunkt mit den Koordinaten
gilt, liegt der Schnittpunkt mit den Koordinaten  auf der Strecke
auf der Strecke  und ist damit ein weiterer Eckpunkt des Dreiecks.
und ist damit ein weiterer Eckpunkt des Dreiecks.
j)
1. Schritt: Lotgerade in  aufstellen
Mit Hilfe des Normalenvektors der Ebenenschar folgt:
aufstellen
Mit Hilfe des Normalenvektors der Ebenenschar folgt:


 2. Schritt: Abstand zur Ebenenschar überprüfen
Mit Hilfe des Lotvektors folgt dann:
Für die Werte
2. Schritt: Abstand zur Ebenenschar überprüfen
Mit Hilfe des Lotvektors folgt dann:
Für die Werte  und
und  hat der Punkt
hat der Punkt  den gewünschten Abstand zu
den gewünschten Abstand zu 
k)
Je größer  ist, desto „höher“ liegt die Ebene
ist, desto „höher“ liegt die Ebene  . Da der Punkt
. Da der Punkt  in der Ebene
in der Ebene  liegt, der Punkt
liegt, der Punkt  in der Ebene
in der Ebene  und der Punkt
und der Punkt  in der Ebene
in der Ebene  folgt
folgt 