Analytische Geometrie 3.1

Haus

Die Abbildung zeigt ein Haus.
Das Koordinatensystem wird so gewählt, dass sich die rechteckige Grundfläche des Hauses achsenparallel in der $x$ - $y$ -Ebene befindet. Gegeben sind die Koordinaten der Punkte $D(0\mid0\mid0)$ , $F(10\mid8\mid4)$ , $G(0\mid8\mid4)$ und $J(10\mid4\mid7)$ . Es gilt: 1 $\;$ LE=1 $\;$ m.

Geometrische Darstellung eines Quaders mit diagonalen Linien und beschrifteten Punkten.

Gib die Koordinaten der Punkte $K$ und $E$ an.

Bestimme eine Gleichung der Ebene $E^*$ , in der die Dachfläche $FGKJ$ liegt, in Koordinatenform.

[Kontrollergebnis: $E^*:3y+4z=40$ ]

Brechne den Neigungswinkel der Dachfläche $FGKJ$ gegenüber einer horizontalen Ebene.

(9P)

Paralleles Licht fällt in Richtung $\overrightarrow{v}=\begin{pmatrix}-\sqrt{39}\\y\\-5\end{pmatrix}$ auf das Hausdach.

Bestimme einen möglichen Wert für $y$ so, dass der Winkel zwischen der Richtung der Lichtstrahlen und der Dachfläche $FGKJ$ 30° beträgt.

(5P)

Ein Drittel der Dachfläche $FGKJ$ wird mit Solarzellen bestückt.

Ermittle die Größe dieser Fläche.

Die Solarzellen können sowohl in der Dachfläche montiert werden als auch in Ebenen $F_a$ , die parallel zur Dachfläche liegen. Dabei darf der Abstand der Ebenen $F_a$ zur Dachfläche maximal 20 $\;$ cm betragen.

Entwickle unter Verwendung des Parameters $a$ eine Gleichung für die Ebenen $F_a$ und gib ein Intervall für die Einschränkung des Parameters $a$ an.

(7P)

Im Innern des Hauses ist auf dem Fußboden $EFGH$ des Dachraumes im Punkt $P(1\mid5\mid4)$ ein 4 $\;$ m langer, senkrecht stehender Mast für eine Satellitenantenne montiert. Dieser Mast ragt durch das Dach ins Freie.

Ermittle die Länge des Teiles dieses Mastes, der sich außerhalb des Hauses befindet.

Berechne den Abstand der Mastspitze $S$ zur Ebene $E^*$ .

(9P)

(30P)

$\blacktriangleright$ Koordinaten der Eckpunkte bestimmen

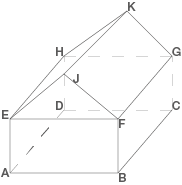
In dieser Aufgabe ist ein Haus mit rechteckiger Grundfläche gegeben, sowie die Punkte $D (0\mid0\mid0)$ , $F (10\mid8\mid4)$ , $G (0\mid8\mid4)$ und $J (10\mid4\mid7)$ .

Du sollst nun die unbekannten Koordinaten der Punkte $K$ und $E$ bestimmen. Ersetze dazu identische Vektoren (parallel und gleich lang), wie zum Beispiel $\overrightarrow{GK}$ durch $\overrightarrow{FJ}$ . Dazu nutzt du, dass der Punkt $D$ im Urpsrung liegt und damit gilt

$\overrightarrow{DG}+ \overrightarrow{GK} = \overrightarrow{DG} + \overrightarrow{FJ} = \overrightarrow{DK} = \overrightarrow{OK}$

und

$\overrightarrow{DA} + \overrightarrow{AE} = \overrightarrow{KJ} + \overrightarrow{AE} = \overrightarrow{DE} = \overrightarrow{OE}$

Damit rechnest du

$\overrightarrow{OK} = \pmatrix{0 \\ 8 \\ 4} + \pmatrix{0 \\ -4 \\ 3}= \pmatrix{0 \\ 4 \\ 7}$

Um den Vektor $\overrightarrow{AE}$ zu berechnen, nutzt du, dass die $z$ - Komponente von $\overrightarrow{AG}$ gerade $\overrightarrow{AE}$ entspricht.

$\overrightarrow{DG} = \pmatrix{0 \\ 8 \\ 4}$

Die $z$ - Komponente dieses Vektors ist $4$ .

Damit erhältst du

$\overrightarrow{OE} = \pmatrix{10\\0\\4}$

Somit sind die Koordinaten der Punkte $E (10 \mid 0 \mid 4)$ und $K(0 \mid 4 \mid 7)$ .

$\blacktriangleright$ Gleichung in Koordinatenform der Dachfläche bestimmen

Du sollst die Koordinatenform der Ebene $E^*$ bestimmen, auf der die Punkte $F,G,K,J$ liegen. Dazu berechnest du zuerst die Parameterform der Ebene.

Wähle zum Beispiel als Stützvektor $\overrightarrow{p} = \overrightarrow{DF} =\overrightarrow{OF} = \pmatrix{10 \\ 8 \\ 4}$

und als Richtungsvektoren

$\overrightarrow{v} = \overrightarrow{OG} - \overrightarrow{p} = \pmatrix{-10\\0\\0}$

$\overrightarrow{w} = \overrightarrow{OJ} - \overrightarrow{p} = \pmatrix{0\\-4\\3}$ .

Du erhältst die Parameterform

$E^*: \overrightarrow{x} = ...$

Vollständige Lösung anzeigen

Die Koordinatenform $a\cdot x + b \cdot y + c\cdot z = C$ erhältst du aus einem Normalenvektor $\overrightarrow{n}$ der Ebene. Diesen kannst du als Kreuzprodukt der Richtungsvektoren berechnen. Die Parameter $a,b,c$ entsprechen dann den Komponenten $n_x,n_y,n_z$ .

Die Konstante entspricht dem Skalarprodukt $\overrightarrow{p}\cdot \overrightarrow{n}$ . Es ergibt sich:

$\overrightarrow{v} \times \overrightarrow{w} = \pmatrix{0 \\ 30\\ 40}$

$\pmatrix{0 \\ 30 \\ 40}\cdot \overrightarrow{p} = 400$ .

Nach Division durch $10$ erhältst du als Komponenten des Normalenvektors

$\pmatrix{n_x = a = 0 \\ n_y = b = 3 \\n_z = c= 4}$

Die Konstante hast du mit $C = 40$ berechnet. Als Koordinatenform erhältst du somit: $E^*: 3\cdot y +4 \cdot z = 40$ .

$\blacktriangleright$ Neigungswinkel des Daches bestimmen

Du sollst den Neigungswinkel $\alpha$ des Daches bestimmen. Dieser entspricht gerade dem Winkel zwischen der Dachebene und der $xy-$ Ebene. Für den Winkel $\alpha$ zwischen zwei Ebenen mit den Normalenvektoren $\overrightarrow{n_1}$ und $\overrightarrow{n_2}$ gilt

$\mathrm{cos}( \alpha) = \dfrac{ \left| \overrightarrow{n_1} \cdot \overrightarrow{n_2} \right|}{\left| \overrightarrow{n_1} \right| \cdot \left| \overrightarrow{n_2} \right|}$

Wähle für $\overrightarrow{n_1}$ den Normalenvektor aus dem vorangegangenen Aufgabenteil und normiere ihn.

$\overrightarrow{n_1}= \dfrac{1}{5} \cdot \pmatrix{ 0 \\ 3 \\ 4}$

Wähle für $\overrightarrow{n_2}$ den Einheitsvektor in $z$ - Richtung.

Du erhältst

$\begin{array}[t]{rll} &\mathrm{cos}(\alpha) &=& \left| \pmatrix{0\\0\\1} \cdot \pmatrix{0\\3\\4} \right | \cdot \dfrac{1}{5} &\quad \\ &\alpha &= &\mathrm{arccos}\left(\dfrac{4}{5}\right)& \\ &\alpha & \approx& 36,9 ^\circ \end{array}$

Also beträgt die Größe des Neigungswinkels ungefähr $36,9 ^\circ$ .

$\blacktriangleright$ Richtung des Lichteinfalls bestimmen

Du hast die Einfallsrichtung $\overrightarrow{v}$ von parallelem Licht mit einem noch unbestimmten Wert $y$ gegeben. Nun musst du den Wert für $y$ so berechnen, dass der Winkel zwischen der Richtung der Lichtstrahlen und der Dachfläche $E^*$ $30 ^\circ$ beträgt.

Das ist gerade der Fall, wenn der Winkel zwischen dem normierten Normalenvektor der Ebene und der normierten Einfallsrichtung des Lichts $90 ^\circ - 30 ^\circ$ beträgt.

Für den Winkel zwischen $\overrightarrow{v}$ und $\overrightarrow{n}$ gilt mit $\mathrm{cos(90 ^\circ - \alpha)} = \mathrm{sin(\alpha)}$ und der Formel aus a)

$\dfrac{\vert \overrightarrow{v} \cdot \overrightarrow{n} \vert}{\vert \overrightarrow{v} \vert \cdot \vert \overrightarrow{n} \vert } = \mathrm{sin}(\alpha)$ .

Einen normierten Normalenvektor hast du bereits mit $\overrightarrow{n} = \pmatrix{0\\3\\4} \cdot \dfrac{1}{5}$ vorher berechnet.

Einsetzen liefert

$y_1 = 0$ und $y_2 = \dfrac{480}{11}$

Vollständige Lösung anzeigen

$\blacktriangleright$ Größe der Dachfläche ermitteln

Nun wird ein Drittel der Dachfläche, die von den Punkten $F,G,K,J$ begrenzt wird, mit Solarzellen bestückt. Um die Größe dieser Fläche zu ermitteln, berechnest du die Beträge der Vektoren $\overrightarrow{a} = \overrightarrow{FJ}$ und $\overrightarrow{b} = \overrightarrow{FG}$ . Der Flächeninhalt ist dann gerade $\, A= \dfrac{1}{3} \cdot \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert$ .

$A = \dfrac{1}{3} \cdot (10 \, \text{m} \cdot 5\, \text{m}) \approx 16,67 \, \text{m}^2$

$\blacktriangleright$ Gleichung der Ebenenschar entwickeln

Diese Solarzellen können sowohl auf dem Dach als auch auf Ebenen montiert werden, die parallel zur Dachfläche mit einem Maximalabstand von $20 \, \text{cm}$ liegen. Nun sollst du eine Gleichung für diese Ebenen entwickeln, in denen du den Parameter $a$ verwendest.

Dazu gehst du so vor: die Gleichung einer zur Dachfläche $E^*$ parallelen Ebene $F_a$ kann durch eine Koordinatenform von $E^*$ beschrieben werden, die um $a$ von der Gleichung der Ebene $E^*$ in Koordinatenform verschoben ist.

$F_a: 3y + 4z = 40 + a$

$\blacktriangleright$ Parameterintervall bestimmen

Den Abstand zweier paralleler Ebenen berechnest du, indem du die Koordinaten eines Punktes auf der einen Ebene in die linke Seite der Hesse - Normalform der anderen Ebene einsetzt. Die Hesse-Normalform der Ebene $F_a$ lautet:

$F_a: \dfrac{3y + 4z - 40 - a}{\sqrt{3^2 + 4^2}} = 0$

Setze also die Koordinaten eines Punktes auf $E^*$ in die Hessesche Normalform der Ebene $F_a$ ein. Mit dem Punkt $F$ erhältst du für den Fall, dass der Abstand positiv ist

$\begin{array}[t]{rll} &d(E^*,F_a)&=& \vert \dfrac{a}{5} \vert &\quad \\ &\dfrac{a}{5} &\leq& 0,2 & \\ &a&\leq&1& \end{array}$

Für den Fall, dass der Abstand negativ ist

$\begin{array}[t]{rll} &\dfrac{a}{5} &\geq& -0,2 & \\ &a&\geq&-1& \end{array}$

Damit ist $-1 \leq a \leq 1$ . Da die Solarzellen nur oberhalb der Dachebene angebracht werden können, gilt also $0 \leq a \leq 1$ .

$\blacktriangleright$ Ermittlung der Länge des freien Satellitenmastes

In diesem Aufgabenteil musst du die Länge eines geraden Satellitenmastes, der senkrecht auf der $xy-$ Ebene steht, außerhalb des Hauses berechnen. Den Verlauf des Mastes kannst du mit einer Geradengleichung modellieren. Bestimme zunächst die Geradengleichung durch den Punkt $P$ . Wähle als Stützvektor dazu den Ortsvektor des Punkes $P$ und als Richtungsvektor den Einheitsvektor in $z$ - Richtung.

$\overrightarrow{g} = \pmatrix{1\\5\\4} + t \cdot \pmatrix{0\\0\\1}$

Bestimme nun den Schnittpunkt dieser Gerade mit der Dachebene. Setze dazu die Geradengleichung in die Koordinatenform der Gleichung der Ebene $E^*$ ein.

$\begin{array}[t]{rll} &3 \cdot 5 + 4\cdot(4+t)=& 40 \\[5pt] &t = \dfrac{9}{4}& \end{array}$

Als Schnittpunkt erhältst du $M(1 \mid 5 \mid 6,25)$ . Vom Punkt $P$ bis zum Punkt $M$ befindet sich der Mast also im Inneren des Hauses. Die Länge dieses Mastteils ergibt sich zu:

$l_{\text{innen}} = 2,25\,\text{m}$

Vollständige Lösung anzeigen

Da der Mast insgesamt $4\,\text{m}$ lang ist, befinden sich $1,75\,\text{m}$ des Mastes außerhalb des Hauses.

$\blacktriangleright$ Abstand zwischen Dachebene und Mastspitze berechnen

Um den Abstand der Mastspitze $S$ zur Ebene $E^*$ zu berechnen, musst du erst die Koordinaten der Mastspitze berechnen.

Weil der Mast ausschließlich in $z$ - Richtung zeigt und insgesamt $4 \, \text{m}$ lang ist, befindet sich $S$ gerade bei $(1 \mid 5 \mid 8)$ . Den Abstand ermitteltst du, indem du die Koordinaten des Punkts $S$ in die linke Seite der Hesseschen Normalform der Gleichung der Ebene $E^*$ einetzt:

$\begin{array}[t]{rll} d(E^*,S)&=& \dfrac{3y+4z-40}{5} \\[5pt] &=& \dfrac{3\cdot 5 +4\cdot 8 -40}{5} \\[5pt] &=& \frac{7}{5} = 1,4 \end{array}$

Also beträgt der Abstand $1,4 \, \text{m}$ .