Teil 1-Analysis
a)
 Parameter
Parameter  ,
,  und
und  bestimmen
bestimmen
 Lösungsweg A: Stammfunktion bestimmen
Lösungsweg A: Stammfunktion bestimmen
Du sollst eine reelle Zahl für die Parameter

,

und

angeben, sodass die Funktionen

,

und

Stammfunktionen der Funktionen

,

und

sind. Stelle dazu jeweils eine Stammfunktion der Funktionen auf und lese die Parameter ab.
Stammfunktion von  berechnen
berechnen
Die Funktionsterme

und

sind dir gegeben. Um den Parameter

zu bestimmen, kannst du eine Stammfunktion von

bestimmen und mit dem Funkionsterm

vergleichen.
Wenn du die beiden Funktionsterme vergleichst, ergibt sich für den Parameter

ein Wert von

.
Stammfunkton von  berechnen
berechnen
Dir ist der Term

und eine Stammfunktion

gegeben. Berechne eine Stammfunktion von

:
Wenn du die beiden Funktionsterme vergleichst, ergibt sich für den Parameter

ein Wert von

.
Stammfunktion von  berechnen
berechnen
Der Funktionsterm

und eine Stammfunktion

ist dir gegeben. Du kannst eine Stammfunktion von

mit Hilfe der linearen Substitution berechnen:
Wenn du die beiden Funktionsterme vergleichst, ergibt sich für den Parameter

ein Wert von

.
Der Wert für

kann einen beliebigen Wert annehmen, da

eine Konstante ist und beim Ableiten wieder wegfällt.
 Lösungsweg B: Ableitung bestimmen
Lösungsweg B: Ableitung bestimmen
Du sollst eine reelle Zahl für die Parameter

,

und

angeben, sodass die Funktionen

,

und

Stammfunktionen der Funktionen

,

und

sind. Berechne dazu jeweils die Ableitung der Funktion und bestimme den Parameter.
Ableitung von  berechnen
berechnen
Die Funktionsterme

und

sind dir gegeben. Um den Parameter

zu bestimmen, kannst du die Ableitung von

bestimmen und mit dem Funkionsterm

.
Wenn du die beiden Funktionsterme vergleichst, ergibt sich für den Parameter

ein Wert von

.
Ableitung von  berechnen
berechnen
Dir ist der Term

und eine Stammfunktion

gegeben. Berechne die Ableitung von

:
Wenn du die beiden Funktionsterme vergleichst, ergibt sich für den Parameter

ein Wert von

.
Ableitung von  berechnen
berechnen
Der Funktionsterm

und eine Stammfunktion

ist dir gegeben. Du kannst die Ableitung von

mit Hilfe der Kettenregel berechnen:
Wenn du die beiden Funktionsterme vergleichst, ergibt sich für den Parameter

ein Wert von

.
 Stammfunktion, deren Graph die
Stammfunktion, deren Graph die  -Achse im Punkt
-Achse im Punkt  schneidet, bestimmen
schneidet, bestimmen
Um die Stammfunktion von

zu bestimmen, deren Graph die

Achse im Punkt

schneidet, setzt du die

- und

-Koordinate in die bereits bestimmte, allgemeine Stammfunktion ein.
Du hast die Konstante

bestimmt. Die gesuchte Stammfunktion ist also

.
b)
 Gleichungssystem zur Berechnung einer ganzrationalen Funktion aufstellen
Gleichungssystem zur Berechnung einer ganzrationalen Funktion aufstellen
Es ist bekannt, dass

eine Nullstelle einer ganzrationalen Funktion dritten Grades ist. Außerdem weißt du, dass

ein Sattelpunkt ist. Du sollst nun ein Gleichungssystem angeben, mit dem man die Koeffizienten bestimmen kann, um die Funktion aufzustellen. Es handelt sich um eine ganzrationale Funktion dritten Grades, diese wird durch die Gleichung
beschrieben. Du benötigst diese Gleichung und ebenfalls die erste und zweite Ableitung:
Nun kannst du dir überlegen, welche Informationen du aus den Bedingungen, dass

eine Nullstelle und

ein Sattelpunkt ist, ablesen kannst.
- Wenn
 eine Nullstelle ist, dann liegt der Graph der Funktion auf dem Punkt
eine Nullstelle ist, dann liegt der Graph der Funktion auf dem Punkt  .
.
- Dir ist der Punkt
 als Sattelpunkt gegeben.
als Sattelpunkt gegeben.
- Die Bedingung für einen Sattelpunkt ist, dass die zweite Ableitung an der Sattelstelle Null sein muss. Deswegen weißt du, dass
 ist.
ist.
- In der Aufgabenstellung ist dir ein Hinweis gegeben, dass ein Sattelpunkt ein Wendepunkt ist, in dem eine zur
 Achse parallele Tangente existiert. Daraus ergibt sich eine weitere Bedingung:
Achse parallele Tangente existiert. Daraus ergibt sich eine weitere Bedingung:  .
.
Du kannst diese Bedingungen nun in die allgemeine Funktionsgleichung und ihre Ableitungen einsetzen und erhältst:
Du kannst das Gleichungssystem noch vereinfachen:
Teil 2-Analytische Geometrie
a)
 Geradengleichung
Geradengleichung  aufstellen
aufstellen
Es ist eine Gerade

gesucht, die durch die Punkte

und

geht. Um die Geradengleichung aufstellen zu können, benötigst du einen Stützvektor, zum Beispiel

und einen Richtungsvektor

. Der Stützvekor ist der Ortsvektor eines Punkts auf der Geraden, der Richtungsvektor ein Verbindungsvektor zweier Punkte auf der Geraden.

=


=

=

Du kannst nun die Geradengleichung aufstellen und erhältst:

.
Eine Gleichung der Geraden

lautet

.
 Geradengleichung
Geradengleichung  aufstellen
aufstellen
Du sollst eine Gleichung einer Geraden

ermitteln, die die Gerade

im Mittelpunkt der Strecke

orthogonal schneidet. Gehe dazu in folgenden Schritten vor:
- Mittelpunkt der Strecke
 berechnen. Diesen kannst du als Stützvektor der Geraden
berechnen. Diesen kannst du als Stützvektor der Geraden  verwenden. Die Formel zur Berechnung des Mittelpunkts lautet
verwenden. Die Formel zur Berechnung des Mittelpunkts lautet  .
.
- Richtungsvektor von
 aufstellen, sodass der der Richtungsvektor orthogonal zum Richtungsvektor von
aufstellen, sodass der der Richtungsvektor orthogonal zum Richtungsvektor von  ist. Damit das gilt, muss das Skalarprodukt der beiden Null sein. Du kannst eine Gleichung mit drei Unbekannten aufstellen, zwei davon wählst du beliebig.
ist. Damit das gilt, muss das Skalarprodukt der beiden Null sein. Du kannst eine Gleichung mit drei Unbekannten aufstellen, zwei davon wählst du beliebig.
- Geradengleichung von
 aufstellen.
aufstellen.
1. Schritt: Mittelpunkt der Strecke  berechnen
berechnen
Du kannst die Ortsvektoren

und

in die Formel zur Berechnung des Mittelpunkts einer Strecke einsetzen:
Der Mittelpunkt der Strecke ist also

. Der Ortsvekor des Mittelpunkts ist eine Möglichkeit für den Stützvektor der gesuchten Geraden

.
2. Schritt: Richtungsvektor von  aufstellen
aufstellen
Der Richtungsvektor der zu bestimmenden Geraden

muss orthogonal zum Richtungsvektor der Geraden

stehen. Zwei Vektoren heißen orthogonal , wenn ihr Skalarprodukt Null ist.
Du kannst für den einen Vektor den Richtungsvektor der Geraden

einsetzen, den anderen bestimmst du für den Fall, dass das Skalarprodukt Null wird. Es gibt dafür unendlich viele Lösungen, bestimme eine davon.
Du erhältst für die Gerade

als möglichen Richtungsvektor

=

.
3. Schritt: Geradengleichung von  aufstellen
aufstellen
Du hast nun den Stützvektor und den Richtungsvektor der Geraden

berechnet und kannst nun die Geradengleichung aufstellen.
Es ergibt sich die Gleichung

.
b)
 Ebenengleichung in Parameterform aufstellen
Ebenengleichung in Parameterform aufstellen
Du hast die Punkte

,

und

gegeben und sollst eine Gleichung der Ebene in Parameterform aufstellen, in der diese drei Punkte liegen.
Die Gleichung dieser Ebene in Parameterform kannst du wie folgt angegeben:
Hierbei versteht man unter
 den Stützvektor der Ebene
den Stützvektor der Ebene  , der die Verschiebung im Raum angibt
, der die Verschiebung im Raum angibt ,
,  die Spannvektoren der Ebene
die Spannvektoren der Ebene  , die die Ebene aufspannen
, die die Ebene aufspannen ,
,  reelle Zahlen, für die die Spannvektoren beliebig lang bzw. kurz werden können und somit alle Punkte auf der Ebene erreicht werden können.
reelle Zahlen, für die die Spannvektoren beliebig lang bzw. kurz werden können und somit alle Punkte auf der Ebene erreicht werden können.
Berechne zunächst den Stützvektor und die Spannvektoren:

=

=


=

=


=

=

Wenn du diese Vektoren nun in die Gleichung einsetzt, erhältst du folgende Ebenengleichung:
.
 Koordinaten der Punkte
Koordinaten der Punkte  und
und  bestimmen
bestimmen
Die Koordinaten der Punkte

und

eines Dreiecks sollen bestimmt werden. Den Scheitelpunkt

hast du gegeben. Außerdem ist eine Gleichung angegeben, mit der ein Innenwinkel des Dreiecks bereits korrekt berechnet wurde:

Der Winkel, der mit dieser Formel berechnet wird, ist der Winkel beim Punkt

. Dies erkennst du daran, dass das

bei der Cosinus-Formel in der Mitte steht.
Die Vektoren

und

sind Verbindungsvektoren vom Punkt

zu einem anderen Eckpunkt. Da du mögliche Koordinaten bestimmen sollst, kannst du auswählen, welcher dieser Vektoren ein Verbindungsvektor von

zu

oder von

zu

ist.
Wähle zum Beispiel

als Verbindungsvektor von

zu

:
Du weißt, dass gilt:

=

-

.
Da du

bestimmen willst, musst du danach auflösen:

=

+

Setze den bekannten Verbindungsvektor

und den Ortsvektor

in die Formel ein:
Du hast somit mögliche Koordinaten für

bestimmt mit

.
Du kannst für die Bestimmung von

nach dem gleichen Prinzip vorgehen. Betrachte nun den anderen Vektor

. Dieser ist nun Verbindungsvektor vom Punkt

zum anderen Eckpunkt

. Du weißt, dass zur Berechnung eines Verbindungsvekotrs gilt:

=

-

.
Da du

suchst, musst du danach umstellen:

=

+

Durch Einsetzen ergibt sich:

Du erhältst als mögliche Koordinaten des Punktes

.
Teil 3-Stochastik
a)
 Fehlende Wahrscheinlichkeiten im Baumdiagramm einzeichnen
Fehlende Wahrscheinlichkeiten im Baumdiagramm einzeichnen
Du kannst die Wahrscheinlichkeiten ergänzen, indem du davon ausgehst, dass die gesamte Wahrscheinlichkeit bei jedem Würfeln

sein muss. Beim ersten Würfeln hast du die Wahrscheinlichkeit

für das Ereignis

gegeben, du weißt also, dass das Ereignis

ebenfalls eine Wahrscheinlichkeit von

hat. Beim zweiten Würfeln hast du für das Ereignis

die Wahrscheinlichkeit

gegeben, somit ist die Wahrscheinlichkeit für


. Dies kannst du für den anderen Zweig übertragen.

 und
und  angeben
angeben
Wenn du die Wahrscheinlichkeit

berechnen willst, musst du beachten, dass es sich hier um eine bedingte Wahrscheinlichkeit handelt, das heißt die Berechnung beginnt ab der Bedingung. Die Bedinung wird immer im Index angegeben. Die Berechnung beginnt also hier bei

für das Ereignis

. Es wird nur einmal gewürfelt, du kannst die Wahrscheinlichkeit

direkt ablesen.
Die Wahrscheinlichkeit für

berechnest du, indem du alle Pfade, die zu

führen verfolgst und nach der Pfadmultiplikationsregel die Wahrscheinlichkeiten innerhalb eines Pfades multiplizierst. Die Wahrscheinlichkeiten verschiedener Pfade werden dann noch nach der Pfadadditionsregel addiert:

=

=

Die Wahrscheinlichkeit

beträgt also

.
 Ereignisse für
Ereignisse für  und
und  formulieren
formulieren
Du sollst dir mögliche Ereignisse

und

überlegen. Dabei musst du darauf achten, dass die Wahrscheinlichkeiten der Ereignisse den auf dem Baumdiagramm eingetragenen Wahrscheinlichkeiten entsprechen. Es ist beschrieben, dass es sich um ein Würfel-Zufallsexperiment handelt. Beim ersten Würfeln ist die Wahrscheinlichkeit für die beiden Ereignisse

und

jeweils

. Es kann hier zum Beispiel zwischen geraden und ungeraden Zahlen unterschieden werden.

steht dann beispielsweise für gerade Zahlen und

für ungerade Zahlen. Beim zweiten Würfeln liegt die Wahrscheinlichkeit für

bei

, für

bei

. Es kann also hier zwischen den Werten der gewürfelten Zahlen unterschieden werden, zum Beispiel Ereignis

steht für die gewürfelten Zahlen

und

.

steht für

und

.
b)
 Werte für
Werte für  und
und  angeben
angeben
Das Ereignis

lautet: Auf dem Titelbild für die Einladung sind genau

Jungen und

Mädchen abgebildet. Du weißt, dass insgesamt

Mädchen und

Jungen beteiligt sind. Du sollst nun mithilfe des Terms:


und

angeben. Du kannst ablesen, dass

den Mädchen zugeordnet werden kann, da insgesamt

Mädchen beteiligt sind. Der untere Wert gibt an, dass

aus

ausgewählt werden, dies entspricht dann dem gesuchten

. Das bedeutet, dass

Mädchen auf dem Titelbild abgebildet werden.
Da

Jungs beteiligt sind, kann ihnen

zugeordnet werden. Das gesuchte

ist also

. Es werden also

von

Jungen auf dem Titelbild abgebildet.
 Anzahl der Möglichkeiten auf dem Titelbild ermitteln
Anzahl der Möglichkeiten auf dem Titelbild ermitteln
Du sollst die Schüler nun so anordnen, dass ein Junge stets zwischen zwei Mädchen steht. Da

Mädchen und nur

Jungen auf dem Titelbild abgebildet werden, müssen die äußersten Positionen von Mädchen eingenommen werden:





Du sollst nun die Anzahl der Möglichkeiten für die Aufstellung bestimmen.
 Lösungsweg A: Ausprobieren
Lösungsweg A: Ausprobieren
Überlege dir dazu, an welchen Stellen die Jungen und Mädchen jeweils stehen können. Du erhältst folgende Fälle:

Fall:






Fall:






Fall:






Fall:






Fall:






Fall:






Fall:






Fall:






Fall:






Fall:






Fall:






Fall:





Es gibt

Möglichkeiten die Schüler anzuordnen.
 Lösungsweg B: Rechnerische Lösung
Lösungsweg B: Rechnerische Lösung
Du hast die Anzahl der Mädchen gegeben, die auf dem Titelbild abgebildet werden, mit

und die Anzahl der Jungen mit

. Um die Anzahl

der möglichen Anordnungen zu bestimmen, kannst du folgende Formel verwenden:

Es gibt

Möglichkeiten die Schüler anzuordnen.
Bildnachweise [nach oben]
© 2016 - SchulLV.
 ,
,  und
und  an, sodass die Funktionen
an, sodass die Funktionen  ,
,  und
und  Stammfunktionen der Funktionen
Stammfunktionen der Funktionen  ,
,  und
und  sind.
Bestimme diejenige Stammfunktion von
sind.
Bestimme diejenige Stammfunktion von  , deren Graph die
, deren Graph die  -Achse im Punkt
-Achse im Punkt  schneidet.
schneidet.
 -Achse parallele Tangente existiert.
-Achse parallele Tangente existiert.
ist die Nullstelle der Funktion.
ist Sattelpunkt des Graphen
 verläuft durch die Punkte
verläuft durch die Punkte  und
und  .
Gib eine Gleichung der Geraden
.
Gib eine Gleichung der Geraden  an.
Ermittle eine Gleichung einer Geraden
an.
Ermittle eine Gleichung einer Geraden  , die die Gerade
, die die Gerade  im Mittelpunkt der Strecke
im Mittelpunkt der Strecke  orthogonal schneidet.
orthogonal schneidet.
 liegen die Punkte
liegen die Punkte  und
und  sowie das Dreieck
sowie das Dreieck  mit dem Punkt
mit dem Punkt  .
Ermittle eine Parametergleichung der Ebene
.
Ermittle eine Parametergleichung der Ebene  .
Mit der Gleichung
.
Mit der Gleichung  hat ein Schüler den Innenwinkel des Dreicks
hat ein Schüler den Innenwinkel des Dreicks  mit dem Scheitelpunkt
mit dem Scheitelpunkt  korrekt berechnet.
Gib für die Punkte
korrekt berechnet.
Gib für die Punkte  und
und  mögliche Koordinaten an.
mögliche Koordinaten an.
 und
und  an.
Formuliere mögliche Ereignisse
an.
Formuliere mögliche Ereignisse  und
und  .
.
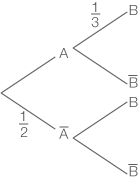 Abb. 1: Baumdiagramm
Abb. 1: Baumdiagramm
 Auf dem Titelbild für die Einladung sind genau
Auf dem Titelbild für die Einladung sind genau  Jungen und
Jungen und  Mädchen abgebildet.
Gib
Mädchen abgebildet.
Gib  und
und  an, wenn
an, wenn  mithilfe des Terms
mithilfe des Terms  korrekt berechnet werden kann.
Auf dem Titelbild sollen die ausgewählten
korrekt berechnet werden kann.
Auf dem Titelbild sollen die ausgewählten  Jungen und
Jungen und  Mädchen so in einer Reihe angeordnet werden, dass ein Junge stets zwischen zwei Mädchen steht.
Ermittle die Anzahl der Möglichkeiten für die Anordnung auf dem Titelbild.
Mädchen so in einer Reihe angeordnet werden, dass ein Junge stets zwischen zwei Mädchen steht.
Ermittle die Anzahl der Möglichkeiten für die Anordnung auf dem Titelbild.
eine Nullstelle ist, dann liegt der Graph der Funktion auf dem Punkt
.
als Sattelpunkt gegeben.
ist.
Achse parallele Tangente existiert. Daraus ergibt sich eine weitere Bedingung:
.
berechnen. Diesen kannst du als Stützvektor der Geraden
verwenden. Die Formel zur Berechnung des Mittelpunkts lautet
.
aufstellen, sodass der der Richtungsvektor orthogonal zum Richtungsvektor von
ist. Damit das gilt, muss das Skalarprodukt der beiden Null sein. Du kannst eine Gleichung mit drei Unbekannten aufstellen, zwei davon wählst du beliebig.
aufstellen.
den Stützvektor der Ebene
, der die Verschiebung im Raum angibt
,
die Spannvektoren der Ebene
, die die Ebene aufspannen
,
reelle Zahlen, für die die Spannvektoren beliebig lang bzw. kurz werden können und somit alle Punkte auf der Ebene erreicht werden können.
 sein muss. Beim ersten Würfeln hast du die Wahrscheinlichkeit
sein muss. Beim ersten Würfeln hast du die Wahrscheinlichkeit  für das Ereignis
für das Ereignis  gegeben, du weißt also, dass das Ereignis
gegeben, du weißt also, dass das Ereignis  ebenfalls eine Wahrscheinlichkeit von
ebenfalls eine Wahrscheinlichkeit von  hat. Beim zweiten Würfeln hast du für das Ereignis
hat. Beim zweiten Würfeln hast du für das Ereignis  die Wahrscheinlichkeit
die Wahrscheinlichkeit  gegeben, somit ist die Wahrscheinlichkeit für
gegeben, somit ist die Wahrscheinlichkeit für 
 . Dies kannst du für den anderen Zweig übertragen.
. Dies kannst du für den anderen Zweig übertragen.
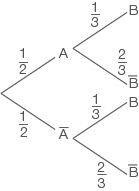 Abb. 1: Baumdiagramm
Abb. 1: Baumdiagramm